目標

在本教程中，您將學習如何使用OpenCV函式應用各種線性濾鏡來平滑影象，例如：

理論

注意

下面的解釋屬於Richard Szeliski和LearningOpenCV的計算機視覺：演算法和應用一書

• 平滑，也稱為模糊，是一種簡單且經常使用的影象處理操作。
• 平滑的原因有很多。在本教程中，我們將重點關注平滑以減少噪音（其他用途將在以下教程中看到）。

• 要執行平滑操作，我們將對影象應用濾鏡。最常見的濾波器型別是線性的，其中輸出畫素的值（即）被確定為輸入畫素值的加權和（即f（i + k，j + 1））：g(i,j)f(i+k,j+l)

  

  被稱為核心，它只不過是過濾器的係數。h （k ，l ）

  它有助於將過濾器視覺化為在影象上滑動的係數視窗。

• 有很多種過濾器，這裡我們會提到最常用的過濾器：

標準化盒式過濾器

• 這個過濾器是最簡單的！每個輸出畫素是其核心鄰居的平均值（它們都以相同的權重貢獻）

• 核心如下：

  

高斯濾波器

• 可能是最有用的過濾器（儘管不是最快）。高斯濾波是通過將輸入陣列中的每個點與高斯核進行卷積，然後將它們相加以產生輸出陣列來完成的。

• 只是為了讓圖片更清晰，還記得一維高斯核心是怎樣的嗎？

  

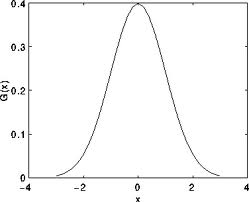
  假設影象是1D，您可以注意到位於中間的畫素將具有最大權重。隨著它們與中心畫素之間的空間距離的增加，其鄰居的權重減小。

  注意

  請記住，2D高斯可以表示為：

  

  其中是平均值（峰值），表示方差（每個變數和）

  中位數過濾器

中值濾波器遍歷訊號的每個元素（在這種情況下是影象），並用其相鄰畫素的中值（位於評估畫素周圍的方形鄰域中）替換每個畫素。

雙邊過濾器

• 到目前為止，我們已經解釋了一些過濾器，主要目標是平滑輸入影象。但是，有時濾鏡不僅可以消除噪音，還可以平滑邊緣。為了避免這種情況（至少在某種程度上），我們可以使用雙邊濾波器。
• 以與高斯濾波器類似的方式，雙邊濾波器還考慮具有分配給它們中的每一個的權重的相鄰畫素。這些權重有兩個分量，第一個是高斯濾波器使用的相同加權。第二個分量考慮了相鄰畫素和評估畫素之間的強度差異。
• 有關更詳細的說明，請檢視
  此連結

碼 

C ++

• 這個程式做了什麼？
  • 載入影象
  • 應用4種不同型別的過濾器（在理論中解釋）並按順序顯示過濾後的影象

• 可下載的程式碼：點選這裡
• 程式碼一目瞭然：

#include <iostream>
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
using namespace std;
using namespace cv;
int DELAY_CAPTION = 1500;
int DELAY_BLUR = 100;
int MAX_KERNEL_LENGTH = 31;
Mat src; Mat dst;
char window_name[] = "Smoothing Demo";
int display_caption( const char* caption );
int display_dst( int delay );
int main( int argc, char ** argv )
{
    namedWindow( window_name, WINDOW_AUTOSIZE );
    const char* filename = argc >=2 ? argv[1] : "../data/lena.jpg";
    src = imread( filename, IMREAD_COLOR );
    if(src.empty())
    {
        printf(" Error opening image\n");
        printf(" Usage: ./Smoothing [image_name -- default ../data/lena.jpg] \n");
        return -1;
    }
    if( display_caption( "Original Image" ) != 0 )
    {
        return 0;
    }
    dst = src.clone();
    if( display_dst( DELAY_CAPTION ) != 0 )
    {
        return 0;
    }
    if( display_caption( "Homogeneous Blur" ) != 0 )
    {
        return 0;
    }
    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        blur( src, dst, Size( i, i ), Point(-1,-1) );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }
    if( display_caption( "Gaussian Blur" ) != 0 )
    {
        return 0;
    }
    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        GaussianBlur( src, dst, Size( i, i ), 0, 0 );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }
    if( display_caption( "Median Blur" ) != 0 )
    {
        return 0;
    }
    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        medianBlur ( src, dst, i );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }
    if( display_caption( "Bilateral Blur" ) != 0 )
    {
        return 0;
    }
    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        bilateralFilter ( src, dst, i, i*2, i/2 );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }
    display_caption( "Done!" );
    return 0;
}
int display_caption( const char* caption )
{
    dst = Mat::zeros( src.size(), src.type() );
    putText( dst, caption,
             Point( src.cols/4, src.rows/2),
             FONT_HERSHEY_COMPLEX, 1, Scalar(255, 255, 255) );
    return display_dst(DELAY_CAPTION);
}
int display_dst( int delay )
{
    imshow( window_name, dst );
    int c = waitKey ( delay );
    if( c >= 0 ) { return -1; }
    return 0;
}

說明 

C ++

讓我們檢查僅涉及平滑過程的OpenCV函式，因為其餘部分現在已經知道了。

規範化塊過濾器：

• OpenCV提供函式以使用此過濾器執行平滑。我們指定4個引數（更多細節，請參閱參考）：
  • src：源影象
  • dst：目標影象
  • 大小（w，h）：定義要使用的核心的大小（寬度為w畫素，高度為h畫素）
  • 點（-1，-1）：表示錨點（被評估的畫素）相對於鄰域的位置。如果存在負值，則將核心的中心視為錨點。

 for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        blur( src, dst, Size( i, i ), Point(-1,-1) );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }

高斯濾波器：

• 它由函式：這裡我們使用4個引數（更多細節，檢查OpenCV引用）：
  • src：源影象
  • dst：目標影象
  • 大小（w，h）：要使用的核心的大小（要考慮的鄰居）。w ^HσXσÿ
  • 
  • 

 for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        GaussianBlur( src, dst, Size( i, i ), 0, 0 );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }

中位數過濾器：

• 這個過濾器由函式提供：我們使用三個引數：
  • src：源影象
  • dst：目標影象，必須與src的型別相同
  • i：核心的大小（只有一個，因為我們使用方形視窗）。一定是奇怪的。

 for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        medianBlur ( src, dst, i );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }

雙邊過濾器

• 由OpenCV函式提供的我們使用5個引數：
  • src：源影象
  • dst：目標影象
  • d：每個畫素鄰域的直徑。
  • ：顏色空間的標準偏差。
  • ：座標空間中的標準偏差（以畫素為單位）

    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    {
        bilateralFilter ( src, dst, i, i*2, i/2 );
        if( display_dst( DELAY_BLUR ) != 0 )
        {
            return 0;
        }
    }

結果

• 程式碼開啟一個影象（在這種情況下是lena.jpg）並在解釋的4個過濾器的效果下顯示它。

• 這是使用medianBlur平滑的影象的快照：