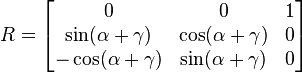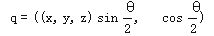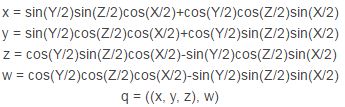參考

一、Unity中的Rotation

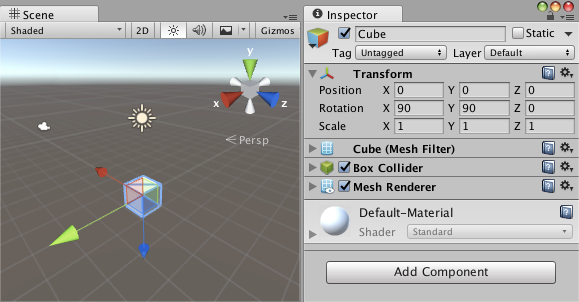
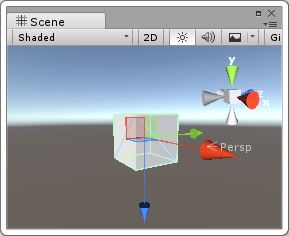
        在unity中，旋轉的表示的常用方法之一，是一個三維向量（x、y、z）：

圖1、Unity中的旋轉

        實際上這是尤拉角。這三個分量分別是繞x軸、y軸、z軸旋轉的角度。

        要對一個object進行旋轉，還可以通過程式碼：

transform.Rotate(x, y, z);

        這裡，如果看過《座標系》一文，就會產生以下兩個疑問：

        1）x軸、y軸、z軸指的是那組基？是世界座標系下的xyz軸，還是本地座標系下的xyz軸？

        2）旋轉的正方向是如何確定的？

        下面分別討論。

二、旋轉軸：靜態尤拉角和動態尤拉角

        首先回答第一個問題：到底哪個是旋轉軸。這又要分為 3種情況。

1、旋轉軸：Editor 中 Transform的旋轉數值

        對這個情況來說，其顯示的旋轉軸既不是世界座標系的座標軸，也不失本地座標系的座標軸。Editor中transform的旋轉軸是父節點的座標軸。這點在editor中看的非常明顯，因此不再贅述。

2、旋轉軸：在script中使用 rotate 函式，在 Space.Self 中旋轉

        Rotate 函式有兩個入參：

public void Rotate(Vector3 eulerAngles, Space relativeTo = Space.Self);
 

        第二個入參的取值有兩種：Space.Self 或者 Space.World。我們先看預設的 Self 的情況。使用下面的一段簡單的程式碼來進行測試：

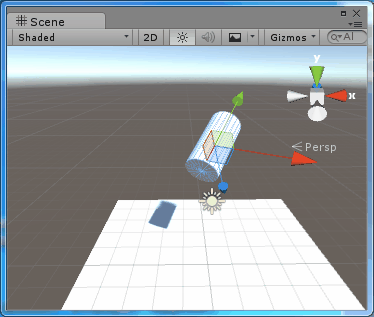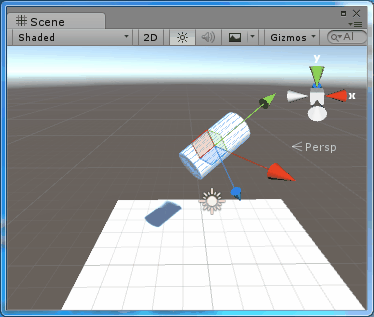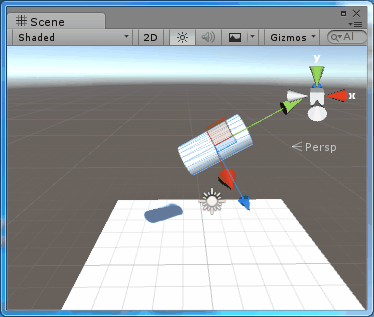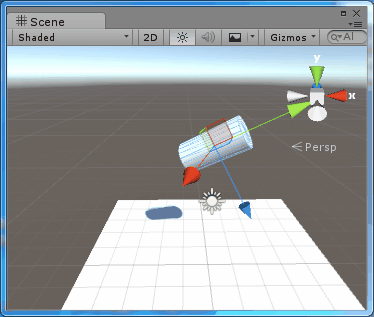
public class TestRotate : MonoBehaviour {

    public Space rotateSpace;

    // Update is called once per frame
    void Update () {
        if (Input.GetKeyDown(KeyCode.R))
            transform.Rotate(new Vector3(0, 10, 0), rotateSpace);
    }
}
 

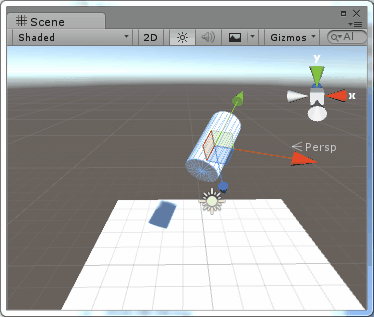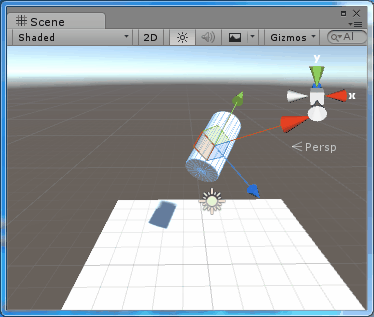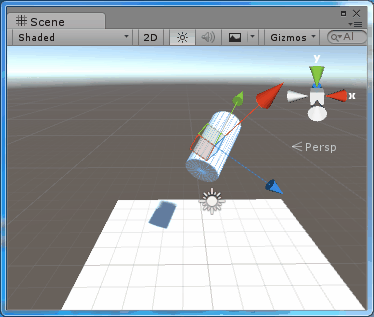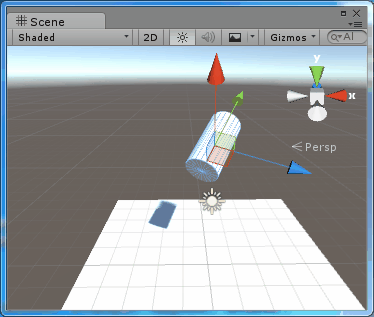        場景中進行測試的是一個圓柱體，其父節點的旋轉為（30，30，0），圓柱體初始的旋轉為（30，0，0），每次按下R鍵，就會在Space.Self 下繞 Y軸旋轉10度，則結果為： 圖2、在Space.Self中旋轉

        可以看到，圓柱體是繞著本地座標系的Y軸旋轉的。使用Space.Self進行旋轉，旋轉軸就是本地座標系的座標軸。

3、在script中使用 rotate 函式，在 Space.World 中旋轉

        下面測試 Space.World 

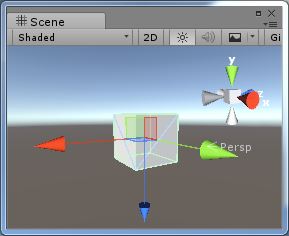
圖3、在Space.World中旋轉

        注意到這裡 Parent 的 Y軸並不是 world 的 Y 軸，而這裡的圓柱體明顯是繞著世界座標系下的 Y 軸旋轉的，所以如程式碼所述，使用Space.World旋轉，旋轉是繞著世界座標系的座標軸旋轉的。

4、靜態尤拉角和動態尤拉角

        前面說到的旋轉軸的問題，在數學上有對應的概念。這就是所謂的靜態尤拉角和動態尤拉角。

        所謂靜態尤拉角，就是其旋轉軸使用的是靜止不動的參考系。動態尤拉角，使用的是剛體本身作為參考系，因而會隨著剛體的旋轉而旋轉。

        因此，再看看前面的三種情況，使用Space.World旋轉，以及 Editor 中的旋轉，是靜態尤拉角；使用Space.self，是動態尤拉角。

三、旋轉的正方向

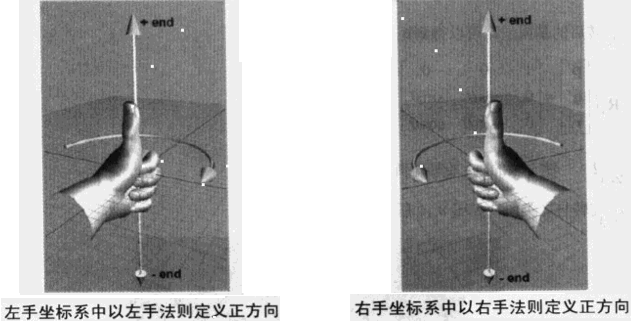
        由於上面的程式碼是每次使得圓柱繞Y軸旋轉10度，因此從上面的動圖就可以看到，是符合左手規則的，即以左手大拇指指向旋轉軸，則四指指向為正方向。

        這其實是當然的：unity的本地座標系和世界座標系都是左手座標系，當然應該使用左手法則。

圖4、旋轉的正方向

四、旋轉的順序

        我們之前使用的旋轉是一個vector3，包含x、y、z三個向量，分別對應著對 X旋轉軸、Y旋轉軸、Z旋轉軸進行旋轉。這裡就又產生了一個問題：他是如何繞著這三個軸旋轉的呢？

        我們也分為靜態尤拉角和動態尤拉角的情況討論。

1、靜態尤拉角

        這種情況對應著上面的editor中顯示的旋轉，以及使用Space.World進行的旋轉。即使旋轉軸保持不變，旋轉的順序也決定了最後的旋轉效果，我們來看下面的例子：

        現在有一個物體擺放在世界中，現在我們要讓他旋轉角度（90，90，0）。現在有兩種方法。

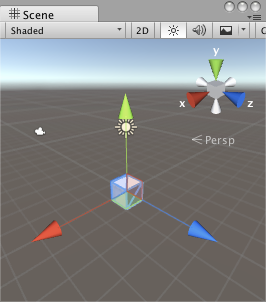
1）首先繞世界座標系的x軸旋轉90度，再繞世界座標系的y軸旋轉90度

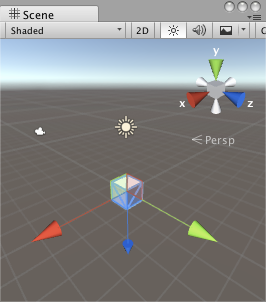
初始狀態	繞x旋轉90度	再繞y旋轉90度

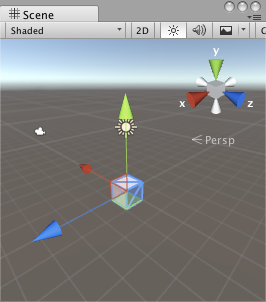
2）首先繞世界座標系的y軸旋轉90度，再繞世界座標系的x軸旋轉90度

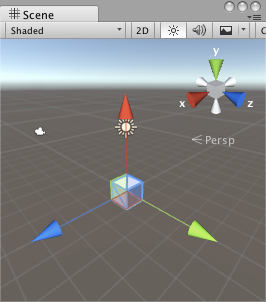初始狀態	繞y軸旋轉90度	再繞x軸旋轉90度

3）旋轉順序的影響

        可以看到，結果完全不同！

        其實從數學上也是可以理解的。在座標系一文中我們說到，座標系變換就相當於乘以變換矩陣，現在的旋轉，實際上就是座標系變換。而矩陣乘法是不滿足交換律的，因此旋轉的順序不能交換，否則會得到不同的結果。

        對於旋轉的順序，一般沒有定式，需要明確指出其順序。對此有一個專門的術語，稱為順規。如果在這個座標系中的旋轉，先繞x軸旋轉，再繞y軸，最後再繞z軸，則稱之為X-Y-Z順規。以此類推。

        對於Unity，從文件中可以看到，使用的是Z-X-Y順規，這是一種常用的順規，可以一定程度上避免萬向節鎖（這一概念我們會在下面討論）。因此在unity中，使用靜態尤拉角旋轉（90，90，0），會得到第1小節中的情況：

圖5、Unity中靜態尤拉角的旋轉順序

2、動態尤拉角

        動態尤拉角除了上面說到的順規問題，還有一個額外的疑問：比如一個物體，初始狀態記為A，以zxy順規旋轉（90，90，0），由於沒有z軸旋轉，第一步當然是繞著當前的x軸旋轉90度，此時狀態記為B，那麼第二步要繞著y軸旋轉90的時候，是繞著初始狀態A時的y軸旋轉，還是繞著此時的B狀態下的y軸旋轉呢？

        首先來看兩者的區別：

1）以初始狀態A時的y軸旋轉：

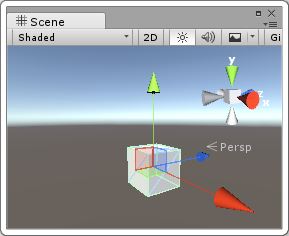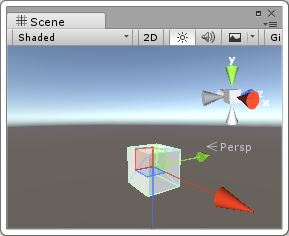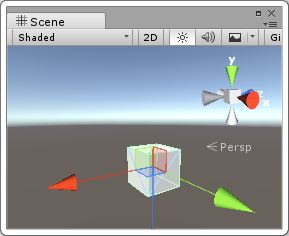初始狀態	繞x軸旋轉90度	繞A狀態的y軸旋轉90度

2）以狀態B下的y軸旋轉：

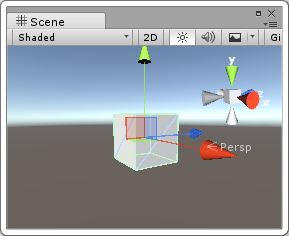初始狀態	繞x軸旋轉90度	繞B狀態的y軸旋轉90度

3）unity中的情況：

        那麼實際中使用的是什麼方式呢？執行以下程式碼，會看到結果如下：

transform.Rotate(new Vector3(90, 90, 0), Space.Self);

圖6、Unity中動態尤拉角的旋轉順序

        可以看到和情況1）相同，所以確認結果為1）。

        如果分兩次旋轉，執行以下程式碼：

transform.Rotate(new Vector3(90, 0, 0), Space.Self);
transform.Rotate(new Vector3(0, 90, 0), Space.Self);

        則效果就和效果2）相同了。 圖7、在Unity中，使用動態尤拉角兩次旋轉

        最終結論是：每次使用Space.self進行rotate時，都是繞著呼叫時刻的座標軸進行旋轉的。

3、靜態尤拉角和動態尤拉角的等價形式

        這裡展開討論一下，靜態尤拉角和動態尤拉角是可以相互轉換的。具體的數學公式可以參考這篇部落格。

        其結論就是：在Space.World中旋轉以 Z-X-Y 歸順旋轉角度（x、y、z），等價於在Space.Self中分別順次旋轉（0，y，0）、（x，0，0）、（0，0，z）。

        從程式碼上來說，就是以下兩段程式碼等價：

    private void Rotate_World(float x, float y, float z) {
        transform.Rotate(x, y, z, Space.World);
    }

    private void Rotate_Self(float x, float y, float z) {
        transform.Rotate(0, y, 0, Space.Self);
        transform.Rotate(x, 0, 0, Space.Self);
        transform.Rotate(0, 0, z, Space.Self);
    }

五、萬向節鎖（Gimbal Lock）

1、什麼是萬向節鎖

        在討論尤拉角旋轉的時候，一個繞不開的話題，就是萬向節鎖。

        對萬向節鎖的定義可以參考這個視訊。簡單來說，就是兩個旋轉軸發生了重合。如下圖：

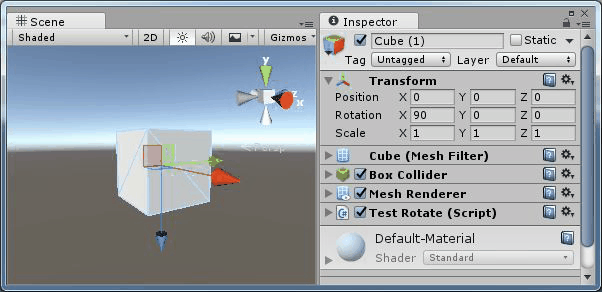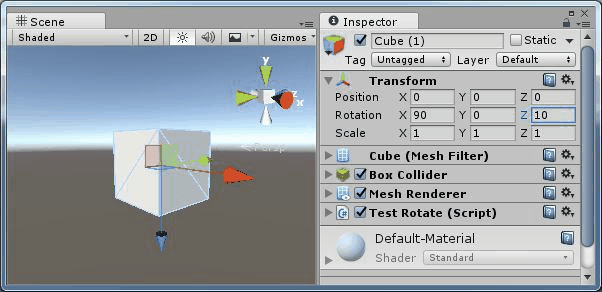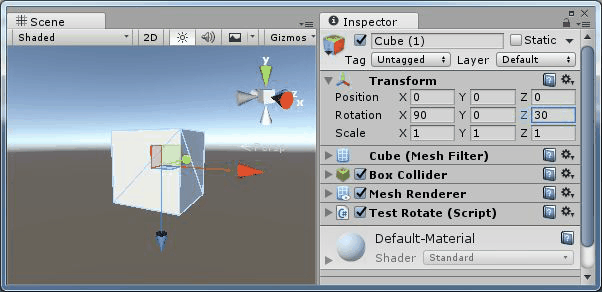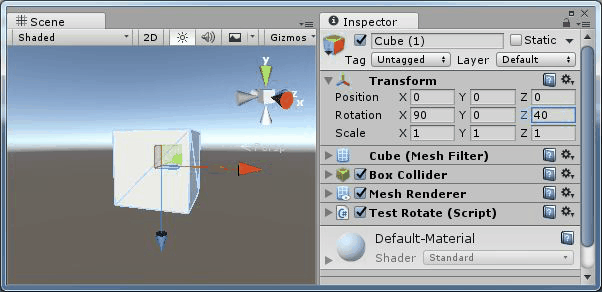旋轉（90，0，z）

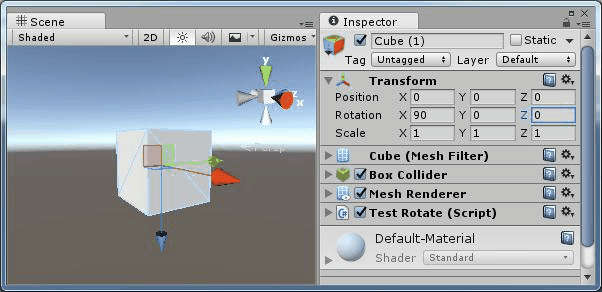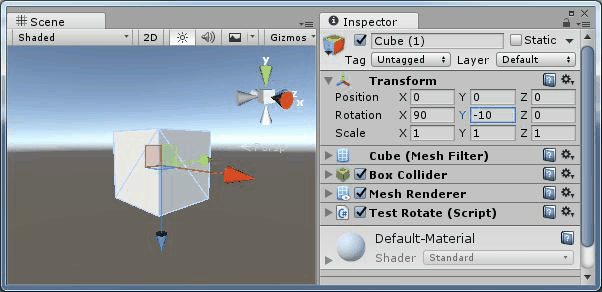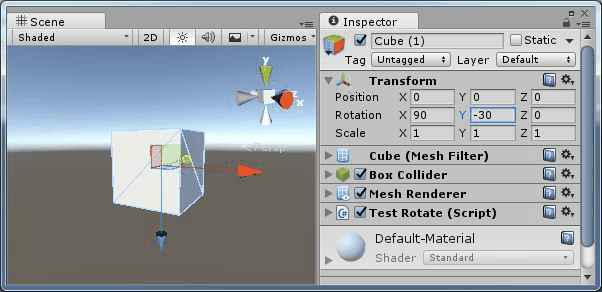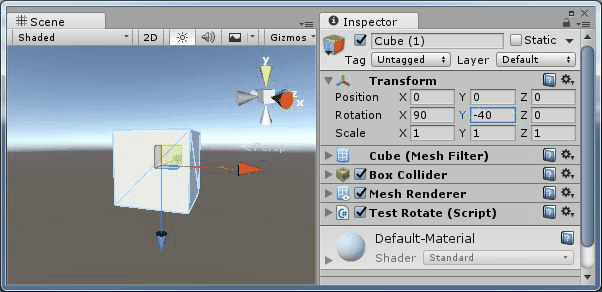旋轉（90，y，0）

        可以看到繞Y軸和繞Z軸旋轉產生的效果是相同的，都是在同一個平面旋轉。即 Y 軸和 Z 軸產生了共線。

        乍一看這很難以理解：在Editor中旋轉是使用的是靜態尤拉角，旋轉軸是固定的，他們兩兩正交，怎麼可能會共線？

        首先我們從直觀上來解釋。這就要說到上面最後一小節的靜態尤拉角和動態尤拉角的互相轉換。注意到Unity中的旋轉是 Z-X-Y 規順，其和使用動態尤拉角 Y-X-Z 規順進行旋轉等價。而經過動態尤拉角（0，y，0）、（90，0，0）的旋轉之後，Z 軸就和初始狀態的 Y軸共線。因此這個時候，繞著 Z 軸旋轉，就和在世界座標系下繞著 Y 軸旋轉產生的效果類似了。

        從數學上也可以解釋這個問題。這裡可以參考CandyCat的文章：

        可以看到第三維不會產生變化，這就是旋轉分量的缺失。

2、如何產生萬向節鎖

        從上面的過程就可以看到，要產生萬向節鎖，只需針對規順的中間的那個座標軸，進行90度的旋轉，就會使得規順前後兩頭的座標軸產生共線。對於Unity中使用的Z-X-Y規順，這個中間的座標軸就是X軸。

3、萬向節鎖的問題

        很多文章中都會提到，產生了萬向節鎖之後，就會導致丟失一個旋轉分量。但實際上，就算產生了如上的萬向節鎖，看似不能在繞著原來的世界座標系的Z軸旋轉，但只要呼叫 Rotate（0，0，z，Space.World），就仍然可以讓該物體旋轉，並不會讓物體無法旋轉。

        實際上，萬向節鎖真正的問題出在做插值動畫的時候。

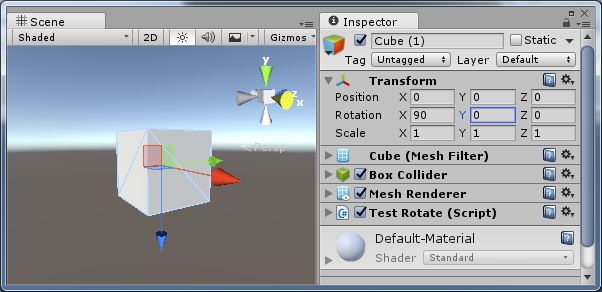
        比如，起始狀態如下，產生了萬向節鎖：

圖8、初始狀態

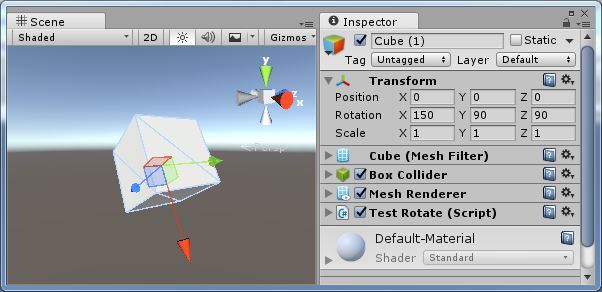
        現在想要讓他旋轉到以下狀態：

圖9、結束狀態

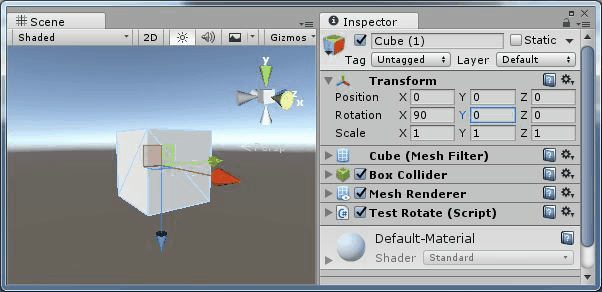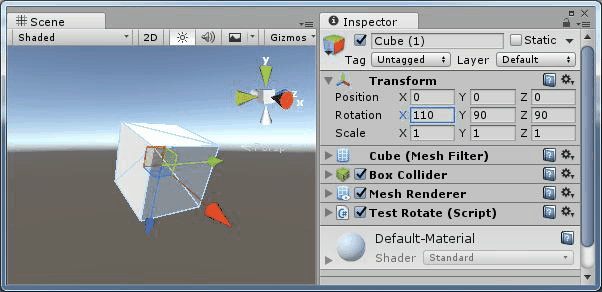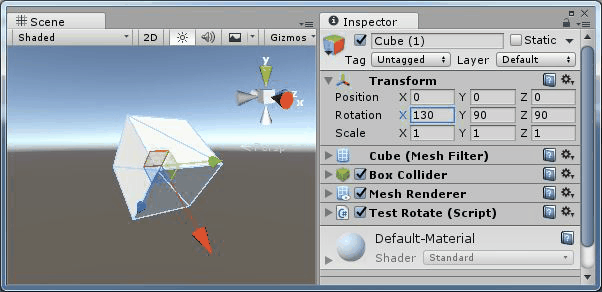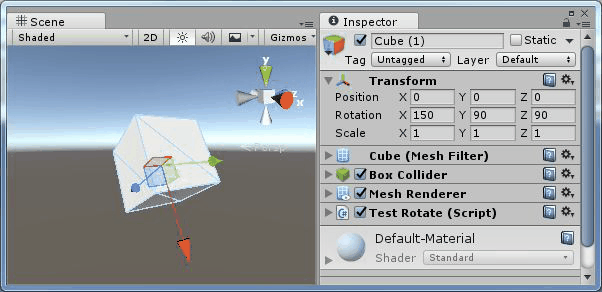
        那麼理想的情況如下：

圖10、期望的旋轉

        但是，注意到由於萬向節鎖的存在，中間旋轉角度（x、y、z）需要產生跳變，那麼如果使用普通的插值，就會要從（90，0，0）到（150，90，90）進行插值，那麼效果如下：

圖11、用尤拉角進行插值

        可以看到，物體會沿著一條弧線進行旋轉。這就是萬向節鎖的問題。

4、在尤拉旋轉中盡力規避萬向節鎖

        前面說到，產生萬向節鎖的關鍵是規順的中間的那條座標軸。只要不繞著這個座標軸旋轉90度，就不會發生旋轉分量丟失的問題。這就是為什麼大多數軟體都將 X 軸作為中間的那條座標軸的原因：常見的旋轉插值是對Camera進行的，而如果繞著X軸旋轉90度，則意味著正向上，或是正向下，這兩種情況都是非常少見的。也就是說，相比於Y軸和Z軸，繞X軸旋轉90度是非常少見的。這樣就可以儘量的避免萬向節鎖。

        但這終歸是指標不治本的方法，另一種完全解決這個問題的方法，就是不再採用尤拉角表示旋轉，這就是我們下面要討論的四元數。

六、Quaternion（四元數）旋轉

1、什麼是四元數

        要表示旋轉，其實一個更直接的方式是使用他的變換矩陣，但是矩陣需要的儲存空間太大，而這個矩陣中有大量的冗餘資料。這就產生了四元數。

        對於四元數的解釋，可以參考CandyCat的文章，寫的非常清楚。這裡摘錄一部分：

        給定一個單位長度的旋轉軸(x, y, z)和一個角度θ。對應的四元數為：

        給定一個Y-Z-X規順的尤拉旋轉(X, Y, Z)，則對應的四元數為：

2、用四元數進行旋轉

        Unity中的四元數支援和一個Vector3相乘，如果把這個Vector3看作一個向量，那麼左乘一個四元數，就相當於對這個向量進行對應的旋轉。