貝葉斯分類器的分類原理是通過某物件的先驗概率，利用貝葉斯公式計算出其後驗概率，即該物件屬於某一類的概率，選擇具有最大後驗概率的類作為該物件所屬的類。也就是說，貝葉斯分類器是最小錯誤率意義上的優化，它遵循“多數佔優”這一基本原則。

一、基本的Bayes分類器實現

這裡將在MATLAB中實現一個可以對兩類模式樣本進行分類的貝葉斯分類器，假設兩個模式類的分佈均為高斯分佈。模式類1的均值向量m1 = (1, 3)，協方差矩陣為S1 =(1.5, 0; 0, 1)；模式類2的均值向量m2 = (3, 1)，協方差矩陣為S2 =(1, 0.5; 0.5, 2)，兩類的先驗概率p1 = p2 = 1/2。詳細的操作包含以下四個部分：

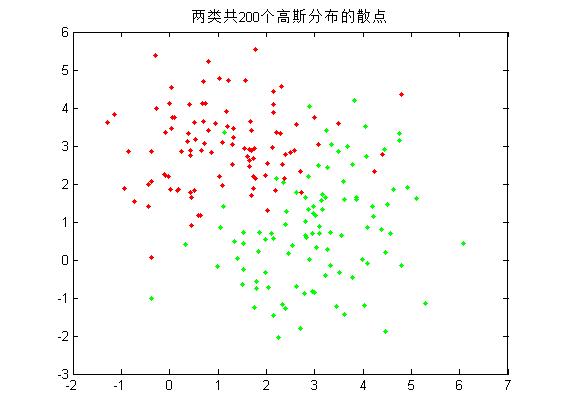
1.首先，編寫一個函式，其功能是為若干個模式類生成指定數目的隨機樣本，這裡為兩個模式類各生成100個隨機樣本，並在一幅圖中畫出這些樣本的二維散點圖；

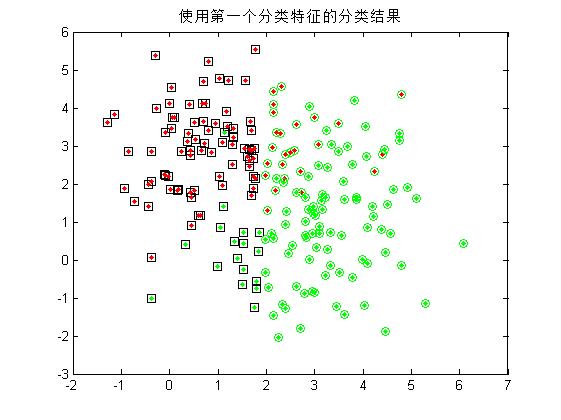
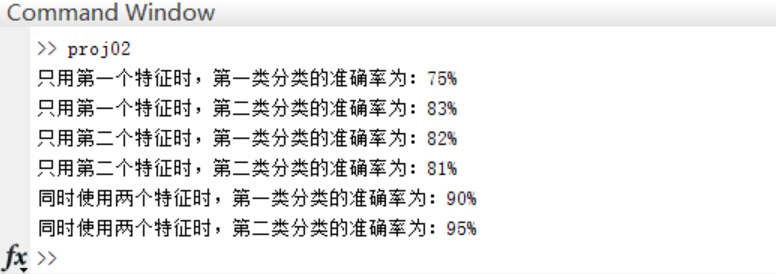
2.由於每個隨機樣本均含有兩個特徵分量，這裡先僅僅使用模式集合的其中一個特徵分量作為分類特徵，對第一步中的200個樣本進行分類，統計正確分類的百分比，並在二維圖上用不同的顏色畫出正確分類和錯分的樣本；（注：綠色點代表生成第一類的散點，紅色代表第二類；綠色圓圈代表被分到第一類的散點，紅色代表被分到第二類的散點！ 因此，裡外顏色不一樣的點即被錯分的樣本。）

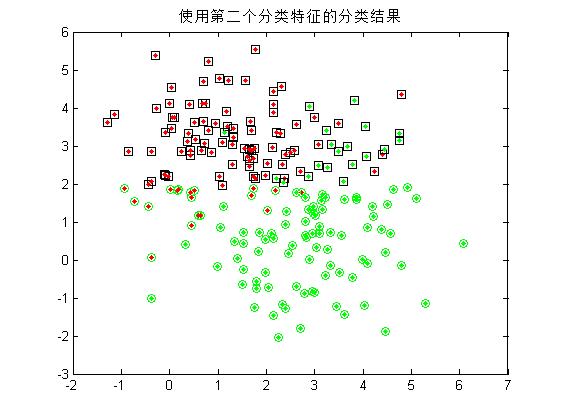
3.僅用模式的第二個特徵分量作為分類特徵，重複第二步的操作；

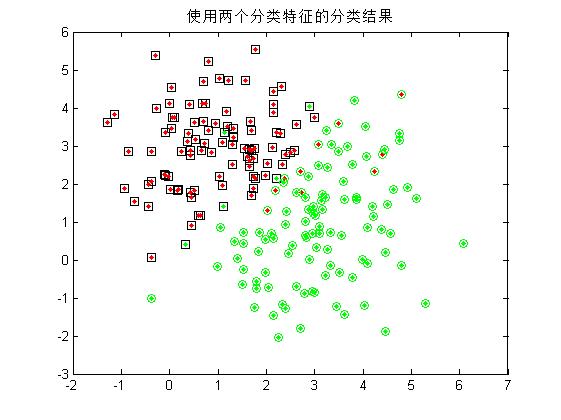
4.同時用模式的兩個分量作為分類特徵，對200個樣本進行分類，統計正確分類百分比，並在二維圖上用不同的顏色畫出正確分類和錯分的樣本；

正確率：

可以看到，單單使用一個分類特徵進行分類時，錯誤率較高（多次試驗均無法得出較好的分類結果），而增加分類特徵的個數是提高正確率的有效手段，當然，這會給演算法帶來額外的時間代價。

二、進一步的Bayes分類器

假設分類資料均滿足高斯分佈的情況下，設計一個判別分類器，實驗目的是為了初步瞭解和設計一個分類器。

1.編寫一個高斯型的Bayes判別函式，該函式輸入為：一給定正態分佈的均值mu、協方差矩陣sigma，先驗概率p以及模式樣本向量X，輸出判別函式的值。

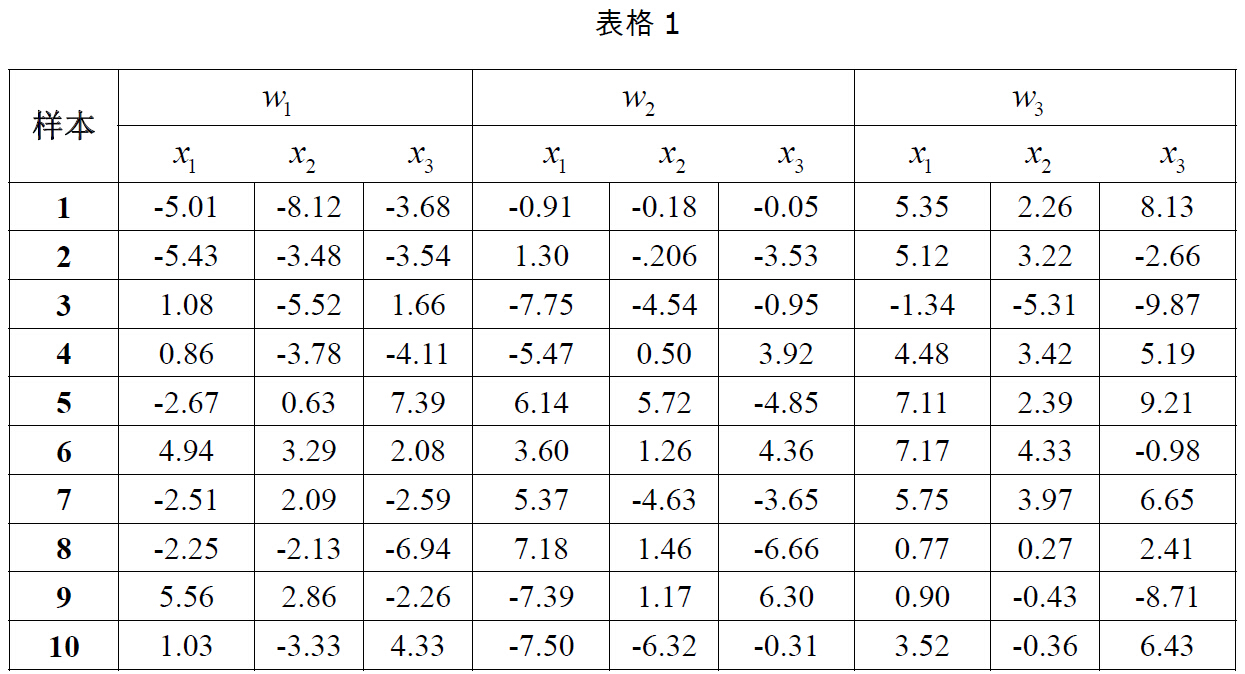
2.以下表格給出了三類樣本各10個樣本點，假設每一類均為正態分佈，三個類別的先驗概率相等均為P(w1)=P(w2 )=P(w3 )=1/3。計算每一類樣本的均值向量和協方差矩陣，為這三個類別設計一個分類器。

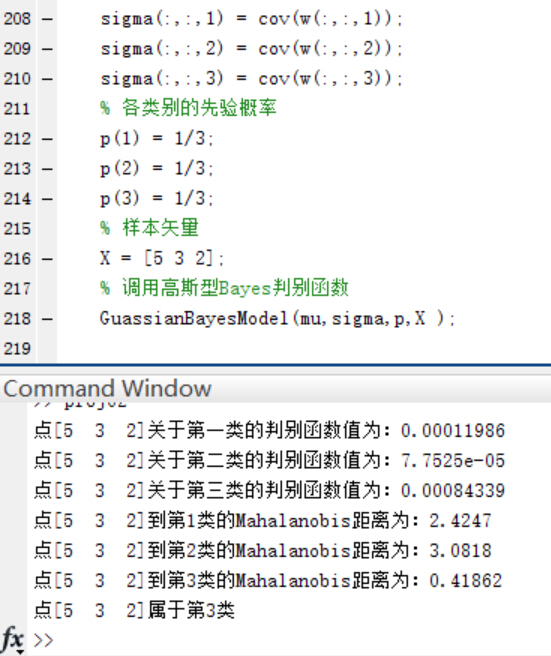
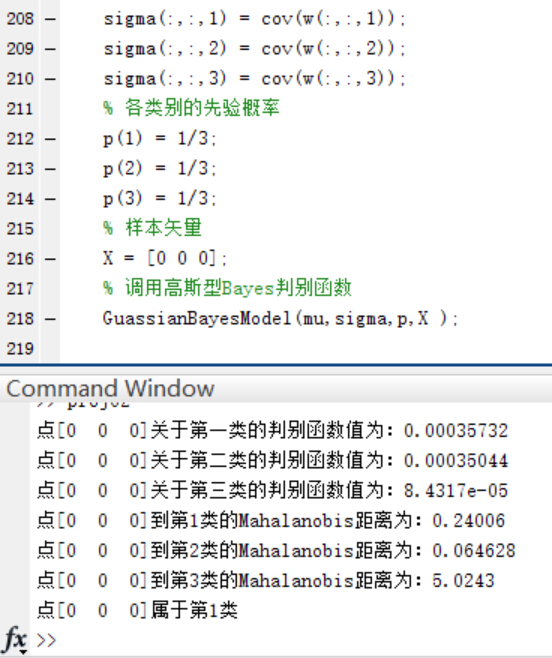
3.用第二步中設計的分類器對以下測試點進行分類：(1,2,1)，(5,3,2)，(0,0,0)，並且利用以下公式求出各個測試點與各個類別均值之間的Mahalanobis距離。以下是來自百度百科的關於馬氏距離的解釋：

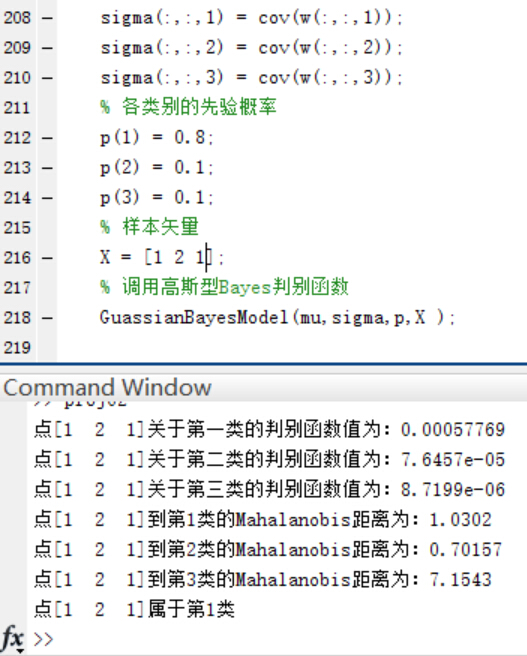
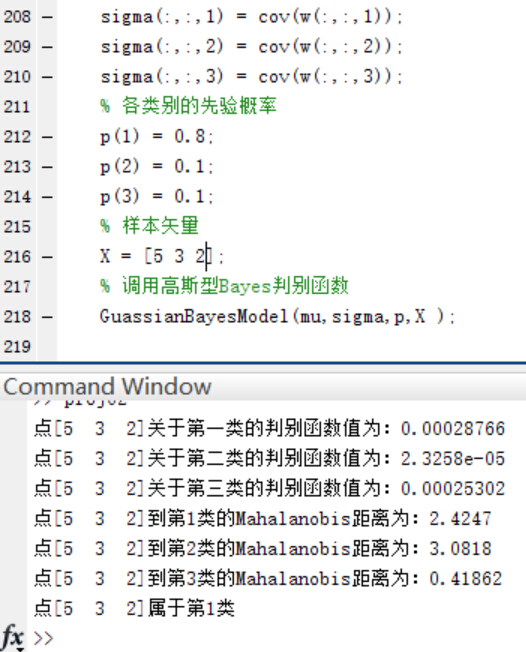
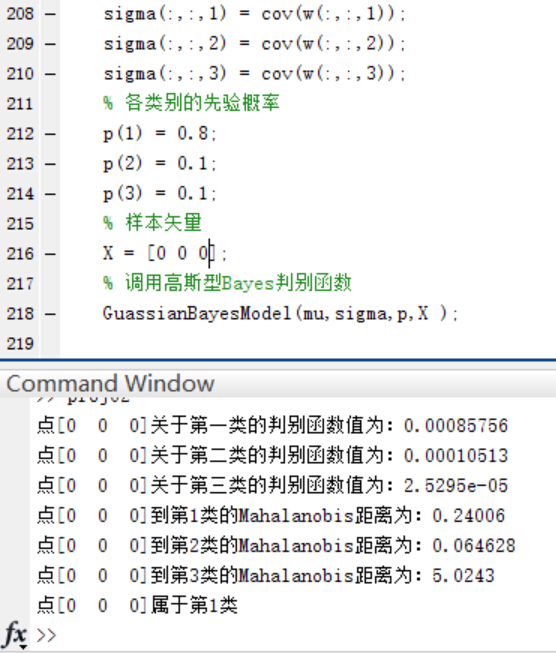
4.如果P(w1)=0.8, P(w2 )=P(w3 )=0.1，再進行第二步和第三步實驗。實驗的結果如下：

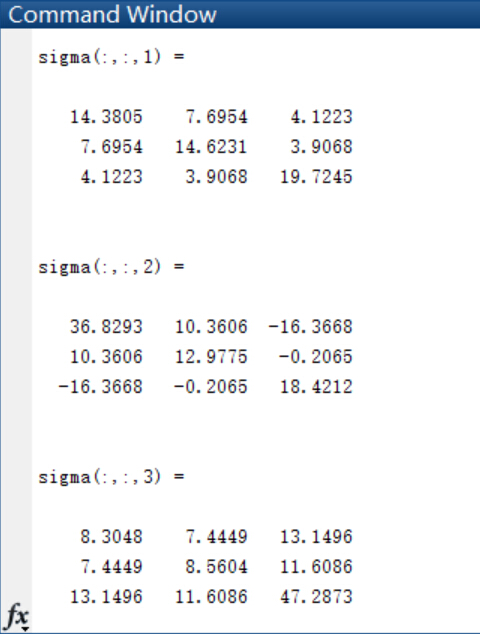
首先是得出三類樣本點各自的均值和協方差矩陣：

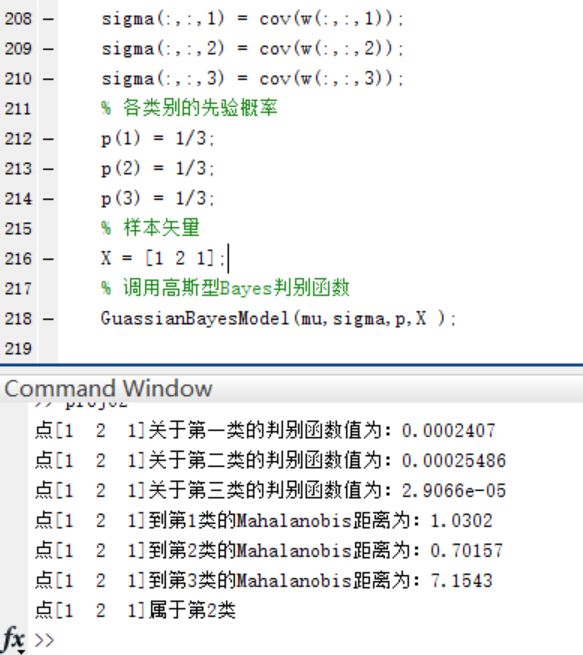
在三個類別的先驗概率均為P(w1)=P(w2 )=P(w3 )=1/3時，使用函式進行分類並給出分類結果和各個測試點與各個類別均值之間的Mahalanobis距離。

驗證當三個類別的先驗概率不相等時，同樣使用函式進行分類並給出分類結果和各個測試點與各個類別均值之間的Mahalanobis距離。

可以看到，在Mahalanobis距離不變的情況下，不同的先驗概率對高斯型Bayes分類器的分類結果影響很大~ 事實上，最優判決將偏向於先驗概率較大的類別。

詳細程式碼在課題組允許公佈後流出~