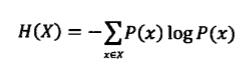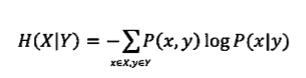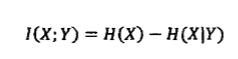就我個人而言覺得資訊的度量是十分難量化的。也的確是這樣，平日一個人說的一句話有多少資訊是很難度量得到的。可是在自然語言處理中，資訊度量的量化又十分重要。《數學之美》一書中吳軍先生舉了一個非常好的例子。他假設了一種情形，他向一個人猜測1-32號足球隊伍中哪支隊伍是世界盃的冠軍，他如果採用五五分的方法逐步縮小範圍那麼需要五次就能知道哪支隊伍是冠軍，假設每向對方詢問一次需要花費一元，那麼誰是世界盃冠軍這條資訊則需要花費五元。而夏農在他的論文“通訊的數學原理”中使用位元來度量資訊量。

其實在上述例子中，是可以優化的。每次的猜測不一定一定要五五分，可以將少數的奪冠熱門分為一組，這樣就可以大大降低猜測需要耗費的次數。當每支隊伍奪冠希望不等時，夏農使用了一個公式來對這種情況的資訊進行度量。

其中H為資訊熵，單位是位元。p1, p2....分別是這32支隊伍奪冠的概率。當概率相同時，資訊的熵就是5位元。而對於隨機變數X，它的熵定義如下：

變數的不確定性越大熵也越大

事物往往是有許多不確定性的，這時需要引入資訊I，當I>U時我們可以說不確定性被消除了，但是當I<U時，只能說這些資訊消除了事物的一部分不確定性。吳軍先生舉了網頁搜尋的例子，當用戶只輸入某些常用關鍵詞，會出來許多的結果，這時需要挖掘隱藏的資訊以確定使用者真正想要查詢的資訊從而給使用者提供正確的網頁。基於上述公式，如果我們知道一些情況Y，那麼在Y條件下X的熵就是

這時可以證明，H(X)>H(X|Y)，也就是二元模型的不確定性要小於一元模型。

現在來談談互資訊的概念，互資訊用於對兩個資訊之間的相關性進行度量，比如“天氣很悶熱”和“要下雨了”這兩條資訊的互資訊就很高。假定有兩個隨機事件X和Y，他們的互資訊定義如下：

其實這個互資訊也可以看作是X的不確定性H(X)以及在知道Y的情況下X的不確定性H(X|Y)之間的差異。也就是

而在機器翻譯中往往需要解決的二義性問題則可以通過這樣的問題解決，比如美國總統Bush是翻譯為人名還是灌木叢，就可以通過該詞的上下文提取相關資訊減小不確定性。如果這個詞的上下文頻繁出現了國會，總統，美國，華盛頓等詞就可當作人名進行翻譯。如果是大量出現土壤、環境等詞則應該當作灌木叢進行翻譯。

最後提提相對熵的概念。相對熵的定義如下

公式比較複雜，但是有些結論是可以直接記住的。

1.對於兩個完全相同的函式，他們的相對熵為0。

2.相對熵越大，兩個函式差異越大；反之，相對熵越小，兩個函式差異越小。

3.對於概率分佈或者概率密度函式，如果取值均大於零，相對熵可以度量兩個隨機分佈的差異性。

本文參照吳軍先生的《數學之美》