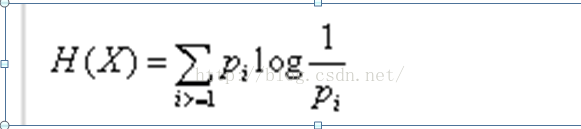資訊是一個很抽象的東西，吃蘋果的概率是二分之一，吃香蕉的概率是二分之一，這裡麵包含了多少資訊量，由於資訊很抽象，無法直觀的量化。

資訊熵原先是熱力學中的名詞，原先含義是表示分子狀態的混亂程度。

夏農引用了資訊熵概念，因此，便有了資訊理論這一門學科，資訊熵表示一個事件或者變數的混亂程度（也可稱為一個事件的不確定性），將資訊變成可以量化的變數。

綜上所述，資訊熵是資訊理論中用於度量資訊量的一個概念。一個系統越是有序，資訊熵就越低；反之，一個系統越是混亂，資訊熵就越高。所以，資訊熵也可以說是系統有序化程度的一個度量。高資訊度的資訊熵是很低的,低資訊度的熵則高。具體說來， 凡是隨機事件導致的變化，都可以用資訊熵的改變數這個統一的標尺來度量。

換一種說法：信我們可以吧資訊熵理解為一個隨機變量出現的期望值，也就是說資訊熵越大，該隨機變數會有更多的形式。資訊熵衡量了一個系統的複雜度，比如當我們想要比較兩門課哪個更復雜的時候，資訊熵就可以為我們作定量的比較，資訊熵大的就說明那門課的資訊量大，更加複雜。

舉個例子：里約奧運會，女子自由泳決賽有兩個國家，美國和中國，中國獲勝的概率是80%，美國獲勝的概率是20%。則誰獲得冠軍的資訊熵=- 0.8 * log2 0.8 - 0.2 * log2 0.2 = 0.257 + 0.464 = 0.721。中國獲勝的機率越高，計算出的熵就越小，即越是確定的情況，不確定性越小，資訊熵越少。如果中國100%奪冠，那麼熵是0，相當於沒有任何資訊。當兩隊機率都是50%最難判斷，所熵達到最大值1。

資訊熵有很多定義，但都類似，簡單來說，就是資訊熵可以衡量事物的不確定性，這個事物不確定性越大，資訊熵也越大就是資訊熵可以衡量事物的不確定性，這個事物不確定性越大，資訊熵也越大。

熵的公式是：

也可以寫成：

借用一本書上的例子

32只球隊共有32種奪冠的可能性，用多少資訊量才能包括這32個結果？按照計算機的二進位制（只有1和0）表示法，我們知道2^5=32 ,也就是需要5符號的組合結果就可以完全表示這32個變化，而這裡的符號通常稱之為位元。既然是這樣，那麼當一件事的結果越不確定時，也就是變化情況越多時，那麼你若想涵蓋所有結果，所需要的位元就要越多，也就是，你要付出的資訊量越大，也即資訊熵越大。當然，每個變化出現的概率不同，因而在夏農的公式中才會用概率，所以資訊熵算的是瞭解這件事所付出的平均資訊量。比如這個例子裡假設32只球隊奪冠可能性相同，即Pi=1/32 ，那麼按照夏農公式計算：

entropy(P1,P2,...,P32)=-(1/32)log(1/32)-(1/32)log(1/32)......-(1/32)log(1/32)=5/32+5/32...+5/32=(5*32)/32=5

資訊熵同樣可以用作資料探勘中（如聚類分析過程），下一節介紹資訊熵在資料探勘中的應用