樸素貝葉斯演算法學習及程式碼示例
阿新 • • 發佈:2019-01-23
最近工作中涉及到文字分類問題,於是就簡單的看了一下樸素貝葉斯演算法(Naive Bayes),以前對該演算法僅僅停留在概念上的瞭解,這次系統的查閱資料學習了一下。樸素貝葉斯演算法以貝葉斯定理為理論基礎,想起大學時學習概率論與數理統計時,老師僅僅講授貝葉斯定理,卻沒有引申講一下樸素貝葉斯演算法。上學時,學習很多數學定理時,心裡都有個疑問,這個到底有什麼用?到底哪些領域用到了這個定理?但是老師往往就是按照所謂的講義、教學大綱授課,如果能做一下引申,相信大家對所學知識會有一個感性認識,理解的也會更深入,相信學習也會更有積極性。
那麼,到底什麼是樸素貝葉斯演算法呢,基本可以一句話概括:貝葉斯定理 + 條件獨立假設。貝葉斯定理就是我們數理統計課上學的定理, P(A|B) = P(B|A) P(A) / P(B);而條件獨立假設指的是:解決分類問題時,會選取很多資料特徵,為了降低計算複雜度,那麼假設資料各個維度的特徵相互獨立。而演算法的計算過程也可以用一句話概括:把計算“具有某特徵的條件下屬於某類”的概率轉換成需要計算“屬於某類的條件下具有某特徵”的概率。整個演算法沒有什麼複雜的計算環節,無非就是計算概率,真的很樸素。由於網路上資料很多,我就不面面俱到的介紹了,下面是我學習該演算法過程中參考的一些連結,有純理論介紹,也有的詼諧幽默介紹。看了下面幾篇文章,樸素貝葉斯演算法應該基本掌握了。 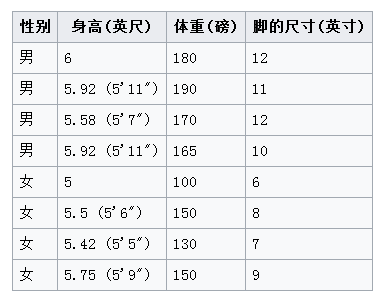


import numpy
from sklearn.naive_bayes import GaussianNB
def test_gaussian_nb():
X = numpy.array([
[6, 180, 12],
[5.92, 190, 11],
[5.58, 170, 12],
[5.92, 165, 10],
[5, 100, 6],
[5.5, 150, 8],
[5.42, 130, 7],
[5.75, 150, 9],
])
Y = numpy.array([1, 1, 1, 1, 0, 0, 0, 0])
gnb = GaussianNB()
gnb.fit(X, Y)
test = numpy.array([6, 130, 8]).reshape(1, -1)
result = gnb.predict(test)
print(result)
print("\n")
result = gnb.predict_proba(test)
print(result[0][0])
print(result[0][1])
if __name__ == '__main__':
test_gaussian_nb()
