01揹包問題在動態規劃中很是常見，那就只簡略概述一下揹包問題：

有一個揹包，承重不能超過m千克，現有n件物品，都有其對應的質量與價值；要求在不超過最大承重的情況下，輸出最大價值；

解決這個問題的最基礎方式是使用二維陣列；行數為其物品的個數（0行空出），列數為0-m；

每一次我們在進行填表時，每一個數都應該有兩次填寫機會，第一次令其等於其上一行同一列的數，而第一次進行更新，即計算此時的重量減去i的重量再加上i的價值和以前那個數誰大（這寓意著在此時揹包的重量下拿出一部分再加上i本身的價值，看看是否能比不裝i時更有價值）；

下面，我們舉出一個例子來看這個問題：
m=4;n=3;
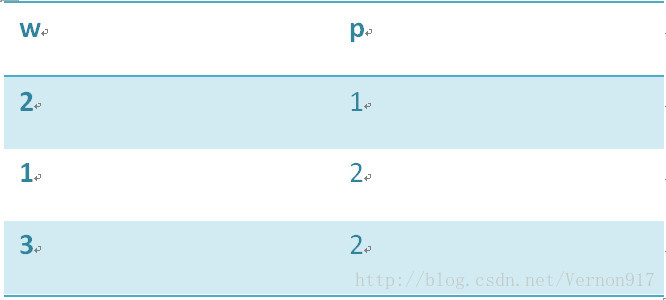
w與p陣列為：

構建而成的二維陣列為：

以下為程式碼：

#include<stdio.h>
#include<string.h> 
#define max(a,b) (a>b? a:b)
int m,n;

int main()
{
    scanf("%d",&m);
    scanf("%d",&n);
    int w[n+1];
    int p[n+1];
    int c[n+1][m+1];
    memset(c,0,sizeof(int)*(n+1)*(m+1));
    for(int i=1;i<=n;++i)
    scanf
 
("%d%d",&w[i],&p[i]);
    for(int i=1;i<=n;++i)
    {
        for(int j=0;j<=m;++j)
        {
            c[i][j]=c[i-1][j];
            if(j-w[i]>=0) 
            c[i][j]=max(c[i][j],c[i-1][j-w[i]]+p[i]);
        }
    }
    printf("%d",c[n][m]);
    return 0;
} 

值得注意的是，我們在建立二維陣列時，可以選擇橫向建立，也可以建立豎向建立（i，j迴圈的先後不同而已），這個無影響；

但也可以選擇從上至下建立，也可以選擇由下至上建立；

這裡選擇由上至下建立，所以為i-1；如果是相反的，那麼應該是i+1；

這裡選擇由上至下的原因，是考慮到空出來的那一行可以使得行標對齊w,p陣列，也可以剛好避免開i-1超出陣列邊界的問題；同樣，如果選擇下至上，也要注意i+1的超界問題；