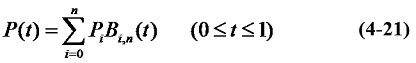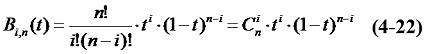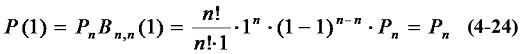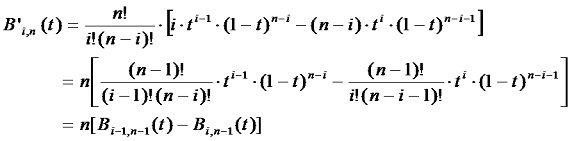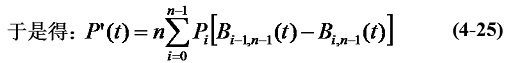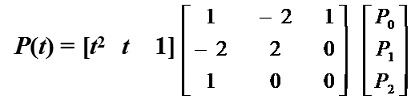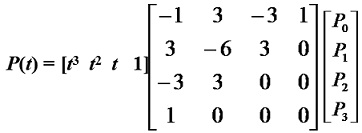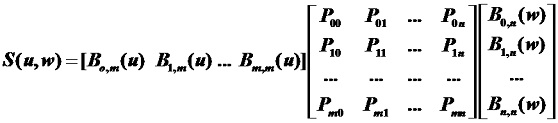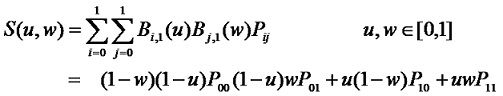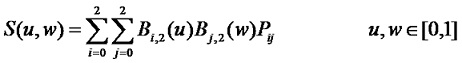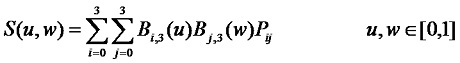(28)Bezier曲線和曲面
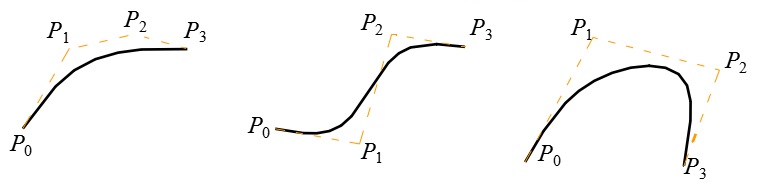
Bezier曲線的形狀是通過一組多邊折線(也稱Bezier多邊形或特徵多邊形)唯一定義出來的。
在多邊折線的各頂點中,只有第一點和最後一點是在曲線上,其餘頂點用來定義曲線的導數、階次和形狀。第一條邊和最後一條邊分別與曲線在起點和終點處相切。曲線形狀趨於多邊折線的形狀。改變多邊折線的頂點位置和曲線形狀的變化有直觀的聯絡。
Bezier曲線的數學表示式定義
n+1個頂點定義一個n次多項式,其引數向量表示式為:
式(4-21)中,Pi為各頂點的位置向量,Bi,n(t)為伯恩斯坦基函式,即Bezier多邊形的各頂點位置向量之間的調和函式。該函式的表示式為:
若規定:00和0!均為1,則當 t=0時:
P(0) = P0B0, n(0) + P1B1,n(0) + P2B2, n(0) +…+ PnBn,n(0)
當t=0時,除第一項外其餘各項均為0,即:
當t =1時:
當t =1時,除最後一項外其餘各項均為0,即:
得出結論:Bezier曲線通過多邊折線的起點和終點。
在起點t =0,式(4-25)中只有i=0, 1兩項有效,即:

同理,在終點t =1,有:P'(1) = n(Pn-Pn-1) (4-27)
得出結論:Bezier曲線在點P0處與邊P0P1相切,在點Pn處與邊Pn-1Pn相切。
Bezier曲線的性質


若保持全部頂點的位置不變,只是把次序顛倒過來,則新的Bezier曲線形狀不變,但方向相反。(表明同一特徵多邊形定義的Bezier曲線是唯一的)
凸包性:
Bezier曲線完全被包容在由特徵多邊形形成的凸包內。
幾何不變性:
Bezier曲線的形狀僅取決於特徵多邊形的頂點,而與座標系的選取無關。
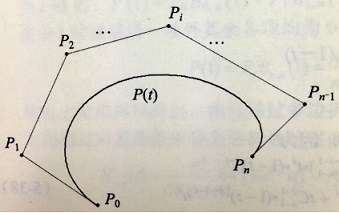
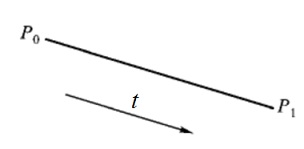
一次Bezier曲線
當n=1時,頂點 P0
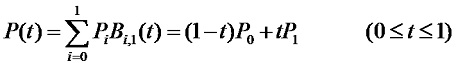
顯然,一次Bezier曲線是一條點P0到點P1的直線段。
當n=2時,頂點P0、P1、P2可定義一條二次(n=2)Bezier曲線。此時式(4-21)可改寫成:
P(t) = (1–t)2P0 + 2t(1–t)P1 + t2P2 (0≤t≤1) (4-28)
寫成矩陣形式為:
二次Bezier曲線
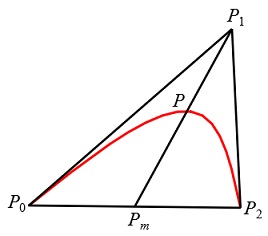
由式(4-28) ,二次Bezier曲線(n=2)在起點P0處有切向量P'0=P'(0)=2(P1–P0);在終點P2處有切向量P'2=P'(1) = 2(P2–P1)。同時,當t =1/2時:
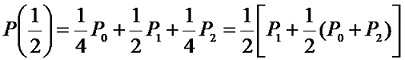
該式說明,二次Bezier曲線經過△P0P1P2中的一條中線P1Pm的中點P。並且可以看出二次Bezier曲線是一條拋物線。
三次Bezier曲線
當n=3時,頂點P0、P1、P2、P3四點可定義一條三次(n=3) Bezier曲線。此時式(4-21)可改寫為:
P(t) = (1–t)3P0+3t(1–t)2P1+3t2(1–t)P2+t3P3
= (1–3t+3t2-t3)P0+ (3t–6t2+3t3)P1+ (3t2–3t3)P2 + t3P3 (0≤t≤1) (4-29)
寫成矩陣表示式為:
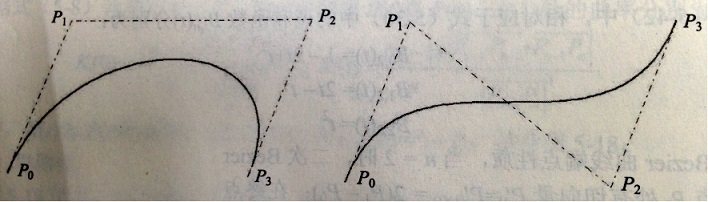
控制點相同但順序不同的三次Bezier曲線
移動控制點P2的Bezier曲線的不同效果
Bezier曲線的控制頂點反求
已知Bezier曲線上給定引數處的位置向量和引數階次,利用Bezier曲線的定義和端點特性,可列出一組方程,求解方程組,可得到相應的控制頂點。
例如:已知三次Bezier曲線上的4個點分別為Q0(120, 0),Q1(45, 0),Q2(0, 45),Q3(0, 120), 它們對應的引數分別為0, 1/3,2/3,1,反求三次Bezier曲線的控制頂點。
由已知條件可得方程組:
Q0 = P0 (t=0)
Q1 = (8/27)P0 + (4/9)P1 + (2/9)P2 + (1/27)P3 (t=1/3)
Q2 = (1/27)P0 + (2/9)P1 + (4/9)P2 + (8/27)P3 (t=2/3)
Q3 = P3 (t=1)
分別將Q0、Q1、Q2、Q3的x、y座標代入方程組求解,可得:
P0(120, 0)
P1(35, -27.5)
P2(-27.5, 35)
P3(0, 120)
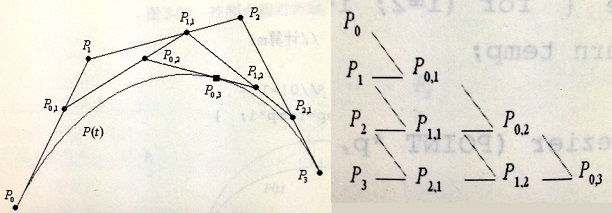
Bezier曲線的幾何作圖法
以控制點數為4,邊數為3的控制多邊形P0P1P2P3為例:
1)分別在邊P0P1、P1P2 、P2P3上找到一點P0,1、P1,1 、P2,1,該點將所在的邊分成 t:(1-t) 兩部分,比如設 t =2/3。
2)然後,將3個分割點構成新的控制多邊形P0,1P1,1P2,1,其控制點數為3,邊數為2;再以同樣的方法及同樣的比例,對邊P0,1P1,1和邊P1,1P2,1進行分割,得到分割點P0,2和P1,2。
3)最後,對邊P0,2P1,2進行相同比例的分割,得到點P0,3。P0,3即為由原控制多邊形P0P1P2P3所確定的三次Bezier曲線上的引數為t 的點P(t)。
4)若讓引數 t 在[0, 1]變動,並且讓△t 取一個較小的增量,如△t =0.1。迴圈多次即可作出三次Bezier曲線。
Bezier曲線的幾何作圖法示意圖以及分割點的遞推關係
Bezier曲線的幾何作圖法總結:
對於任意控制多邊形,在以PiPi+1為端點的第 i條邊上,找一點Pi,1(t),把該邊分成t:(1-t) 比例,則分割點Pi,1(t)=(1-t)Pi + tPi+1 (i=0,1,…,n-1),這n個點組成一個新的n-1邊形,對該多邊形重複上述操作,得到一個新的n-2邊形的頂點Pi,2(t) (i=0,1,…,n-2),依次類推,連續作n次後,得到一個單點Pi,n(t),該點就是Bezier曲線上引數為t的點P(t),讓t 在[0, 1]變動,就得到Bezier曲線。
Bezier曲線的拼接
設有兩條Bezier曲線P(u)和Q(w),P(u)由P0P1P2…Pm定義,Q(w)由Q0Q1Q2…Qn定義: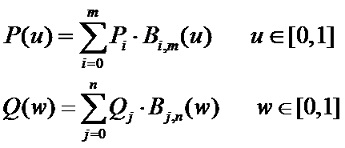
考慮兩條Bezier曲線的一階連續性(C1和G1)拼接設計:
1)由端點切向量條件:
P’(1)=m(Pm-Pm-1) Q’(0)=n(Q1-Q0)
2)若曲線P(u)與Q(w)首尾拼接達到G1連續,必有Pm與Q0重合,並且Q’(0)=lP’(1) (l >0),即:
Q0=Pm Q1=Q0+(λm/n)*(Pm-Pm-1)
3)上式的幾何意義:P(u)與Q(w)兩條Bezier曲線拼接達到G1連續時,控制點Pm-1、Pm(=Q0)和Q1在一條直線上。
4)當λ=1時,P(u)與Q(w)兩條Bezier曲線拼接可達到C1連續。
兩條Bezier曲線的拼接示意圖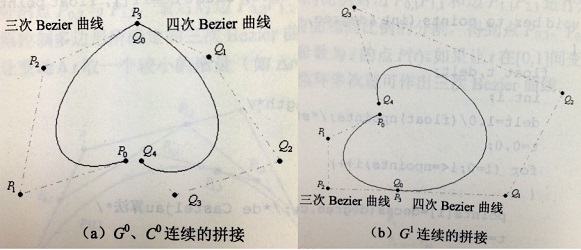
Bezier曲面
設Pij (i=0,1,…,m; j=0,1,…n)為(m+1)×(n+1)個空間點列,則m×n次Bezier曲面定義為: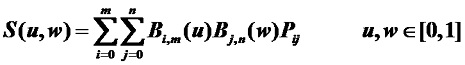
其中,
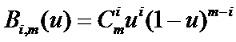 和
和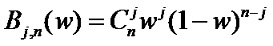 是Bernstein基函式。
是Bernstein基函式。依次用線段連線點陣 Pij 中相鄰兩點所形成的空間網格,稱為特徵網格。
Bezier曲面的矩陣表示為:
1、雙線性Bezier曲面
當m=n=1時,定義一張雙線性Bezier曲面:
2、雙二次Bezier曲面
當m=n=2時,定義一張雙二次Bezier曲面,其邊界曲線及引數座標曲線均為拋物線:
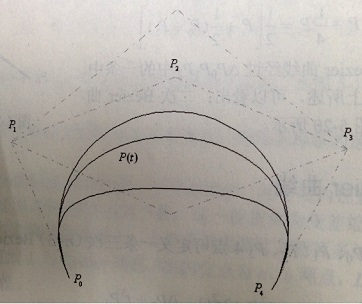
3、雙三次Bezier曲面
當m=n=3時,定義一張雙三次Bezier曲面,它由16個頂點定義,引數曲線u、v都是三次Bezier曲線,該曲面只通過4個角點P00、P30、P03、P33: