xgboost

• 簡介
  xgboost 的全稱是eXtreme Gradient Boosting，由華盛頓大學的陳天奇博士提出，在Kaggle的希格斯子訊號識別競賽中使用，因其出眾的效率與較高的預測準確度而引起了廣泛的關注。

• 與GBDT的區別
  GBDT演算法只利用了一階的導數資訊，xgboost對損失函式做了二階的泰勒展開，並在目標函式之外加入了正則項對整體求最優解，用以權衡目標函式的下降和模型的複雜程度，避免過擬合。所以不考慮細節方面，兩者最大的不同就是目標函式的定義，接下來就著重從xgboost的目標函式定義上來進行介紹。

• xgboost的模型

xgboost對應的模型就是一堆CART樹。一堆樹如何做預測呢？就是將每棵樹的預測值加到一起作為最終的預測值，可謂簡單粗暴。

下圖就是CART樹和一堆CART樹的示例，用來判斷一個人是否會喜歡計算機遊戲：

第二圖的底部說明了如何用一堆CART樹做預測，就是簡單將各個樹的預測分數相加。

• 目標函式
  xgboost的目標函式定義如下：

  

  其中，t表示第t輪，表示第t輪所生成的樹模型，表示正則項，。接下來是xgboost的重點，我們使用二階泰勒展開

  

  來定義一個近似的目標函式如下：

  

  因為的值由之前的過程決定，所以本輪不變，constant也不影響本輪的訓練，所以將這兩者其去掉，得到：

  

  現在的目標函式有一個非常明顯的特點，它只依賴於每個資料點在誤差函式上的一階導數和二階導數。接下來，我們對
  的定義做一下細化，將樹拆分成結構部分q和葉子權重部分w：

  

  當我們給定了如上定義之後，就可以對樹的複雜度進行定義了：

  

  其中，第一部分中的T為葉子的個數，第二部分為w的L2模平方。我們來看下圖的示例：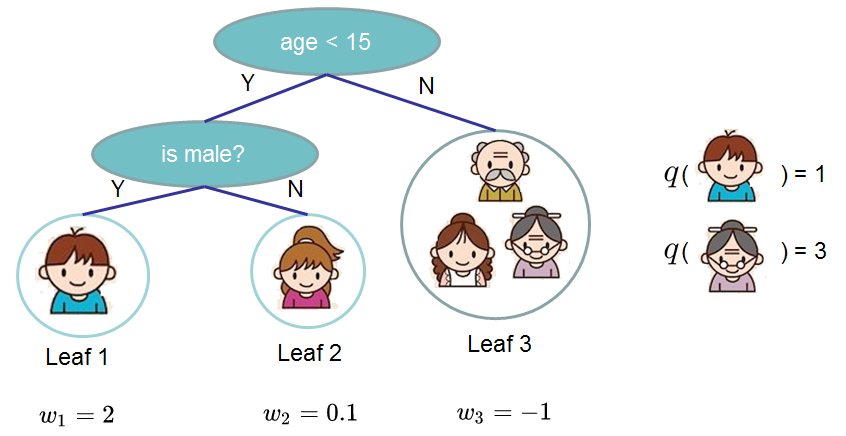

  

  
  可以看到葉子的權重w就是GBDT例子中葉子結點的值，而q就是將某個樣本點對映到某個葉子結點的函式。有了上邊的兩個式子後，繼續對目標函式進行如下改寫：

  

  其中，為每個葉子節點上的樣本集合。現在這個目標函式包含了T個相互獨立的單變數二次函式，我們定義：

  

  那麼我們就得到了最終的目標函式樣子：

  

  現在我們假設q已知，通過將上式對w求導並令其等於0，就可以求出令最小的w：

  

  此時目標函式 的值為：

  

  
  剩下的工作就很簡單了，通過改變樹的結構來找到最小的，而對應的結構就是我們所需要的結果。不過列舉所有樹的結構不太可行，所以常用的是貪心法，每一次嘗試去對已有的葉子加入一個分割。對於一次具體的分割，我們可以獲得的增益可以由如下公式計算：

• 問題是：樹的結構近乎無限多，一個一個去測算它們的好壞程度，然後再取最好的顯然是不現實的。所以，我們仍然需要採取一點策略，這就是逐步學習出最佳的樹結構。這與我們將K棵樹的模型分解成一棵一棵樹來學習是一個道理，只不過從一棵一棵樹變成了一層一層節點而已。下面我們就來看一下具體的學習過程。
  我們以上文提到過的判斷一個人是否喜歡計算機遊戲為例子。最簡單的樹結構就是一個節點的樹。我們可以算出這棵單節點的樹的好壞程度obj*。假設我們現在想按照年齡將這棵單節點樹進行分叉，我們需要知道：
  1、按照年齡分是否有效，也就是是否減少了obj的值
  2、如果可分，那麼以哪個年齡值來分。

  為了回答上面兩個問題，我們可以將這一家五口人按照年齡做個排序。如下圖所示：

  

  按照這個圖從左至右掃描，我們就可以找出所有的切分點。對每一個確定的切分點，我們衡量切分好壞的標準如下：

  

  這個Gain實際上就是單節點的obj*減去切分後的兩個節點的樹obj*，Gain如果是正的，並且值越大，表示切分後obj*越小於單節點的obj*，就越值得切分。同時，我們還可以觀察到，Gain的左半部分如果小於右側的γ，則Gain就是負的，表明切分後obj反而變大了。γ在這裡實際上是一個臨界值，它的值越大，表示我們對切分後obj下降幅度要求越嚴。這個值也是可以在xgboost中設定的。

  掃描結束後，我們就可以確定是否切分，如果切分，對切分出來的兩個節點，遞迴地呼叫這個切分過程，我們就能獲得一個相對較好的樹結構。

  注意：xgboost的切分操作和普通的決策樹切分過程是不一樣的。普通的決策樹在切分的時候並不考慮樹的複雜度，而依賴後續的剪枝操作來控制。xgboost在切分的時候就已經考慮了樹的複雜度，就是那個γ引數。所以，它不需要進行單獨的剪枝操作。

  
  觀察xgboost的目標函式會發現如下三點：
  • 這個公式形式上跟ID3演算法（採用entropy計算增益） 、CART演算法（採用gini指數計算增益） 是一致的，都是用分裂後的某種值減去分裂前的某種值，從而得到增益
  • 引入分割不一定會使情況變好，因為最後有一個新葉子的懲罰項。所以這也體現了預減枝的思想，即當引入的分割所帶來的增益小於一個閾值時，就剪掉這個分割
  • 上式中還有一個係數λλ，是正則項裡ww的L2模平方的係數，對ww做了平滑，也起到了防止過擬合的作用，這個是傳統GBDT裡不具備的特性

• 總結
  xgboost與傳統的GBDT相比，對代價函式進行了二階泰勒展開，同時用到了一階與二階導數，而GBDT在優化時只用到一階導數的資訊，個人認為類似牛頓法與梯度下降的區別。另一方面，xgboost在損失函式里加入的正則項可用於控制模型的複雜度。正則項裡包含了樹的葉子節點個數、每個葉子節點上輸出score的L2模的平方和。從Bias-variance tradeoff角度來講，正則項降低了模型的variance，使學習出來的模型更加簡單，防止過擬合，這也是xgboost優於傳統GBDT的一個特性。

xgboost的優化：

1. 在尋找最佳分割點時，考慮傳統的列舉每個特徵的所有可能分割點的貪心法效率太低，xgboost實現了一種近似的演算法。大致的思想是根據百分位法列舉幾個可能成為分割點的候選者，然後從候選者中根據上面求分割點的公式計算找出最佳的分割點。
2. xgboost考慮了訓練資料為稀疏值的情況，可以為缺失值或者指定的值指定分支的預設方向，這能大大提升演算法的效率，paper提到50倍.
3. 特徵列排序後以塊的形式儲存在記憶體中，在迭代中可以重複使用；雖然boosting演算法迭代必須序列，但是在處理每個特徵列時可以做到並行。
4. 按照特徵列方式儲存能優化尋找最佳的分割點，但是當以行計算梯度資料時會導致記憶體的不連續訪問，嚴重時會導致cache miss，降低演算法效率。paper中提到，可先將資料收集到執行緒內部的buffer，然後再計算，提高演算法的效率。
5. xgboost 還考慮了當資料量比較大，記憶體不夠時怎麼有效的使用磁碟，主要是結合多執行緒、資料壓縮、分片的方法，儘可能的提高演算法的效率。

xgboost的優勢：

1、正則化

• 標準GBM的實現沒有像XGBoost這樣的正則化步驟。正則化對減少過擬合也是有幫助的。 
  實際上，XGBoost以“正則化提升(regularized boosting)”技術而聞名。

2、並行處理

• XGBoost可以實現並行處理，相比GBM有了速度的飛躍，LightGBM也是微軟最新推出的一個速度提升的演算法。 XGBoost也支援Hadoop實現。

3、高度的靈活性

• XGBoost 允許使用者定義自定義優化目標和評價標準 。

4、缺失值處理

• XGBoost內建處理缺失值的規則。使用者需要提供一個和其它樣本不同的值，然後把它作為一個引數傳進去，以此來作為缺失值的取值。XGBoost在不同節點遇到缺失值時採用不同的處理方法，並且會學習未來遇到缺失值時的處理方法。

5、剪枝

• 當分裂時遇到一個負損失時，GBM會停止分裂。因此GBM實際上是一個貪心演算法。XGBoost會一直分裂到指定的最大深度(max_depth)，然後回過頭來剪枝。如果某個節點之後不再有正值，它會去除這個分裂。 
  這種做法的優點，當一個負損失（如-2）後面有個正損失（如+10）的時候，就顯現出來了。GBM會在-2處停下來，因為它遇到了一個負值。但是XGBoost會繼續分裂，然後發現這兩個分裂綜合起來會得到+8，因此會保留這兩個分裂。

6、內建交叉驗證

• XGBoost允許在每一輪boosting迭代中使用交叉驗證。因此，可以方便地獲得最優boosting迭代次數。 
  而GBM使用網格搜尋，只能檢測有限個值。

7、在已有的模型基礎上繼續

• XGBoost可以在上一輪的結果上繼續訓練。 
  sklearn中的GBM的實現也有這個功能，兩種演算法在這一點上是一致的。

Reference