一類問題：對於一個整數n，將n進行質因數分解

演算法1：

根據定義直接列舉，直接給出程式碼：

void Decom(int n) {
    int i;
    vector<int> res;
    for(i = 2; i <= n; i++) {
        while(n%i == 0) {
            res.push_back(i);
            n /= i;
        }
    }
    for(i = 0; i < res.size()-1; i++) printf("%d*", res[i]);
    printf
 
("%d\n", res.back());
}

演算法2：

考慮到若有i滿足n % i == 0，則必有n % (n/i) == 0，所以可以僅列舉i從2到n√，程式碼如下：

void Decom(int n) {
    int i;
    vector<int> res;
    for(i = 2; i*i <= n; i++) {
        while(n%i == 0) {
            res.push_back(i);
            n /= i;
        }
    }
    for(i = 0; i < res.size()-1
 
; i++) printf("%d*", res[i]);
    printf("%d\n", res.back());
}

Pollard-Rho演算法：

該演算法需要使用的大素數判定的Miller-Rabin演算法，之前已經討論過。
Miller-Rabin演算法戳這裡
對於一個大整數n，我們取任意一個數x使得x是n的質因數的機率很小，但如果取兩個數x1以及x2使得它們的差是n的因數的機率就提高了，如果取x1以及x2使得gcd(abs(x1−x2),n)>1的概率就更高了。這就是Pollard-Rho演算法的主要思想。

對於滿足gcd(abs(x1−x2),n)>

其中判斷素數就使用Miller-Rabin演算法。

那麼我們怎樣不斷取得x1和x2呢？
x1在區間[1,n]中隨機出來，而x2則由x[i]=(x[i-1]*x[i-1]%n+c)%n推算出來，其中c為任意給定值，事實證明，這樣就是比較優的。

程式碼如下：

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;

const int MAXN = 65;
long long x[MAXN];
vector<long long> f;

long long multi(long long a, long long b, long long p) {
    long long ans = 0;
    while(b) {
        if(b&1LL) ans = (ans+a)%p;
        a = (a+a)%p;
        b >>= 1;
    }
    return ans;
}

long long qpow(long long a, long long b, long long p) {
    long long ans = 1;
    while(b) {
        if(b&1LL) ans = multi(ans, a, p);
        a = multi(a, a, p);
        b >>= 1;
    }
    return ans;
}

bool Miller_Rabin(long long n) {
    if(n == 2) return true;
    int s = 20, i, t = 0;
    long long u = n-1;
    while(!(u & 1)) {
        t++;
        u >>= 1;
    }
    while(s--) {
        long long a = rand()%(n-2)+2;
        x[0] = qpow(a, u, n);
        for(i = 1; i <= t; i++) {
            x[i] = multi(x[i-1], x[i-1], n);
            if(x[i] == 1 && x[i-1] != 1 && x[i-1] != n-1) return false;
        }
        if(x[t] != 1) return false;
    }
    return true;
}

long long gcd(long long a, long long b) {
    return b ? gcd(b, a%b) : a;
}

long long Pollard_Rho(long long n, int c) {
    long long i = 1, k = 2, x = rand()%(n-1)+1, y = x;
    while(true) {
        i++;
        x = (multi(x, x, n) + c)%n;
        long long p = gcd((y-x+n)%n, n);
        if(p != 1 && p != n) return p;
        if(y == x) return n;
        if(i == k) {
            y = x;
            k <<= 1;
        }
    }
}

void find(long long n, int c) {
    if(n == 1) return;
    if(Miller_Rabin(n)) {
        f.push_back(n);
        return;
    }
    long long p = n, k = c;
    while(p >= n) p = Pollard_Rho(p, c--);
    find(p, k);
    find(n/p, k);
}

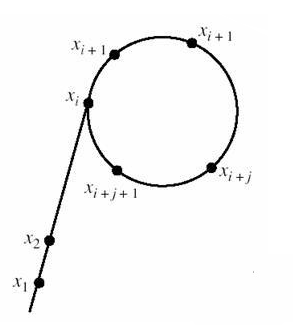
關於此演算法名稱的來歷：
由於該演算法在推算x[i]時，最後必定會出現x[i+j]=x[i]，然後把x[i]按照一種神奇的方式寫下來，就會長得像希臘字母ρ。。。
如下圖：

然後發明者叫做Pollard，所以就叫做了這樣一個神奇的名字。。