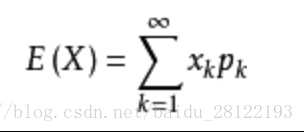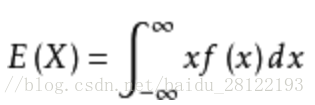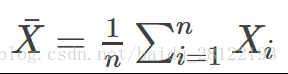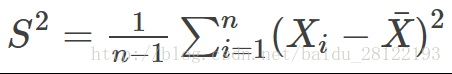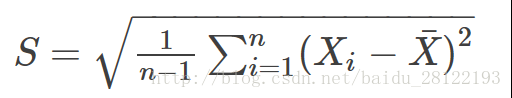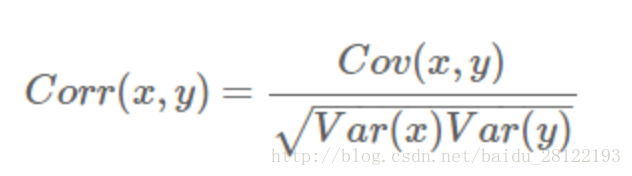首先說明一下，本文是本人在複習方差等相關知識的過程中，通過網路上的相關講解，進行個人總結後得到的，並非個人原創，在此釋出只是為了作為一個學習記錄與大家分享。

1.期望

      試驗中可能出現的值及其概率的乘積，即是數學期望

  1)離散型

離散型隨機變數的一切可能的取值Xi與對應的概率p(Xi)乘積之和稱為該離散型隨機變數的數學期望(若該求和絕對收斂)，記為E(X)。它是簡單算術平均的一種推廣，類似加權平均。

   2)連續型

      設連續性隨機變數X的概率密度函式為f(x)，若積分絕對收斂，則稱積分的值為隨機變數的數學期望，記為E(X)。

期望的一些性質：

a.E(C)=C

b.E(CX)=CE(X)

c.E(X+Y)=E(X)+E(Y)

d.當X和Y相互獨立時，E(XY)=E(X)E(Y)

2.方差

     方差用於反映觀察值與平均值之間的偏離程度，通過方差可以看出一組資料的離散程度

     求方差時，首先需要先求出資料的平均值，然後再求解方差，公式如上！

3.標準差

      標準差即方差開平方

4.協方差

        協方差用於衡量兩個變數的總體誤差；

        如果兩個變數的變化趨勢一致，也就是說如果其中一個大於自身的期望值時另外一個也大於自身的期望值，那麼兩個變數之間的協方差就是正值；如果兩個變數的變化趨勢相反，即其中一個變數大於自身的期望值時另外一個卻小於自身的期望值，那麼兩個變數之間的協方差就是負值。

       如果X與Y是統計獨立的，那麼二者之間的協方差就是0，因為兩個獨立的隨機變數滿足E[XY]=E[X]E[Y]。

5.相關係數

       其中的Var(x)就是方差D(x)，這是方差的兩種表示方式

       相關關係是一種非確定性的關係，相關係數是研究變數之間線性相關程度的量。由於研究物件的不同。

       當然也可以將相關係數看作隨機變數標準化後的協方差

         1）當相關係數ρ=1時，隨機變數X和Y之間存線上性關係，且為正線性相關

      2）當相關係數ρ=−1時，兩者之間為負線性關係

     3）|ρ|≤1，線性相關性隨著|ρ|的減小而減小。當|ρ|=0時，兩者之間就不存線上性關係了

      注意：

      當|ρ|=0，隨機變數X和Y是不線性相關的，但不能代表兩者相互獨立，    

      他們之間可能存在別的相關關係；但當X和Y相互獨立時，它們的相關係

      數|ρ|=0。可以說，|ρ|=0是X和Y相互獨立的必要不充分條件。

      但是，當隨機變數(X,Y)服從二維正態分佈時，則X和Y不相關等價於兩者

      相互獨立