題目描述：

給定n個矩陣{A1,A2,…An},其中Ai 與Ai+1 是可乘的，i = 1,2,3…n-1。考查這n 個矩陣的連乘積A1A2….An。
比如A1A2A3,可以有(A1A2)A3，A1(A2A3) 這兩種方式。

思路:

若使用窮舉搜尋法，其複雜度是隨著n的增長呈指數增長的，可以使用動態規劃的時候，即求其最優子結構。設AiAi+1…Aj記作A[i : j]，設A[i : j]，1 <= i <= j <= n,所需要的最少數乘次數為m[i][j].則有：
m[i][j] = 0, i = j;
m[i][j] = min{m[i][k] + m[k+1][j] + pi - 1pkpj }, i < j .
s[][]用來記錄最優解的位置，最後通過遞迴的方式，確定最後的計算次序。
首先要明確的是：所給出的矩陣必須是可以連乘的！
下面給出我們假設要計算的資料是，A1A2A3A4A5A6，其中A1：30*35，A2：35*15，A3：15*5，A4：5*10，A5：10*20，A6：20*25
所以我們的p陣列的值為，p[] = {30,35,15,5,10,20,25};

程式碼：

要理解m，s的意義，以及在取最優解的時候的操作。可以在紙上模擬一下，還是比較好理解的。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

// m[i][j]:從第i個數組到第j個數組，求最優值陣列，s[][]：最優斷開位置的陣列
//n 表示測試陣列的個數
int matrixChan(int *p,int n, int **m, int **s)
{
//  int n = strlen(p);
    for(int i = 1; i <= n; i ++)
        m[i][i] = 0
 
;
    for(int r = 2; r <= n; r ++) //r為連乘矩陣的個數 
    {
        for(int i = 1; i <= n - r + 1; i ++)
        {
            int j = i + r - 1;  // i 表示起始，j表示第r個 
            m[i][j] = m [i + 1][j] + p[i - 1]*p[i]*p[j];
            s[i][j] = i;
            for(int k = i + 1; k < j; k ++)  //在第一個到第r個數組連乘，尋找最優的斷開點 
 

            {
                int t = m[i][k] + m[k + 1][j] + p[i - 1]*p[k]*p[j];
                if(t < m[i][j])
                {
                    m[i][j] = t;
                    s[i][j] = k;
                }
            }
        }
    }
    return m[1][n]; // 返回第一個到第n個，即題目給出資料的答案 
}

void traceback(int **s, int i, int j)
{
    if(i == j)
        return;
    traceback(s, i, s[i][j]);
    traceback(s, s[i][j] + 1, j);
    printf("Multiply A %d,%d and A %d,%d\n", i,  s[i][j] ,(s[i][j] + 1), j );
}

int main()
{
    int p[6];
    p[0] = 30;   
    p[1] = 35;     
    p[2] = 15;     
    p[3] = 5;     
    p[4] = 10;     
    p[5] = 20;    
    p[6] = 25;     
    //new出測試的陣列。 
    int **m, **s;
    int n = 7;
    m = (int **)malloc(n*sizeof(int *));
    s = (int **)malloc(n*sizeof(int *));

    for (int i = 0; i < n; i++)
    {
        m[i] = (int *)malloc(n*sizeof(int));  
        s[i] = (int *)malloc(n*sizeof(int));
    }

    int ans = matrixChan(p,6, m, s);
    printf("%d\n",ans);
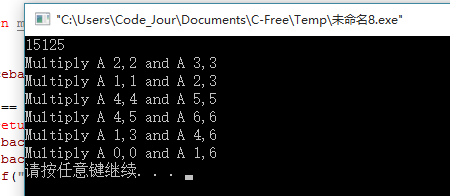
    traceback(s, 0, 6);
}

結果：

從最後的結果可以看出，最優的次數是15125，然後最優的計算次序是(（A1(A2A3)) ((A4A5)A6)) .

Matrixchain的計算量取決於r，i，k的迴圈，為O(n3)，空間複雜度為O(n2)。相比與窮舉搜尋更加高效。

尾巴：

不知道為啥，最近失眠超級嚴重的，特別是週六的晚上，於是乎，寫完這篇已經快凌晨4點了，而我還是毫無睡意。

大三、、、、2015、11、01 03：45