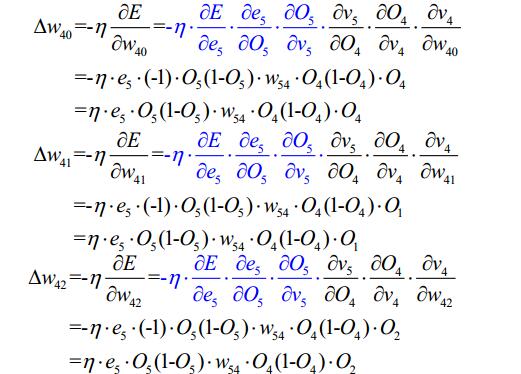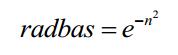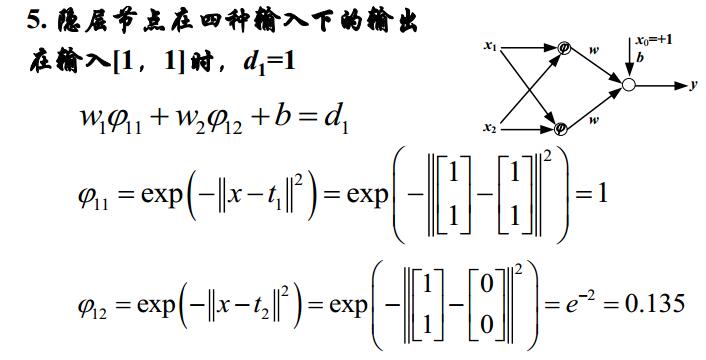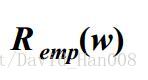ANN(人工神經網路)基礎知識
ANN是一個非線性大規模並行處理系統
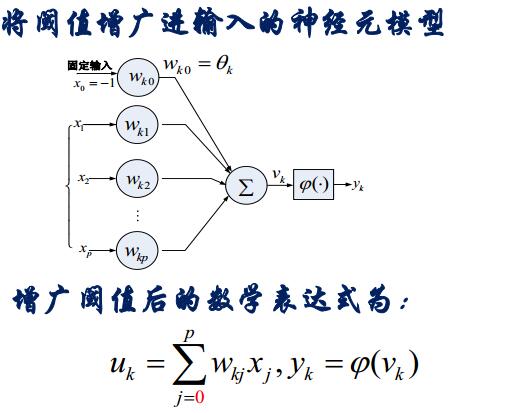
1.1人工神經元的一般模型
神經元的具有的三個基本要素
1、一組連線,連線的強度由個連線上的權值表示,若為正,則表示是啟用,為負,表示,抑制
2、一個求和單元:用於求各個輸入訊號的加權和
3、一個非線性啟用函式:起到非線性對映的作用,並將神經元輸出幅度限制在一定的範圍內,一般限制在(0,1)或者(-1,1)之間
此外還有一個閾值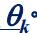
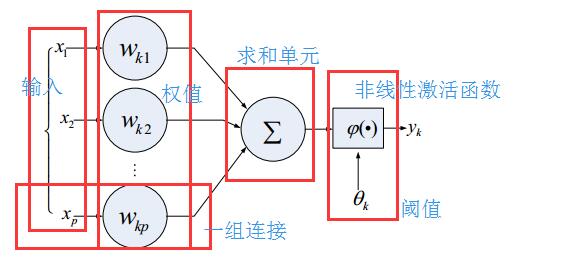
求和部分
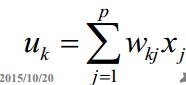
總和減去閾值
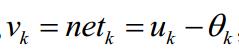
減去後的值經過線性啟用函式
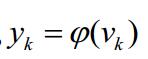
得到輸出Yk
將上面這個過程進行簡化:
啟用函式的種類
1.1.1閾值函式(M-P模型)
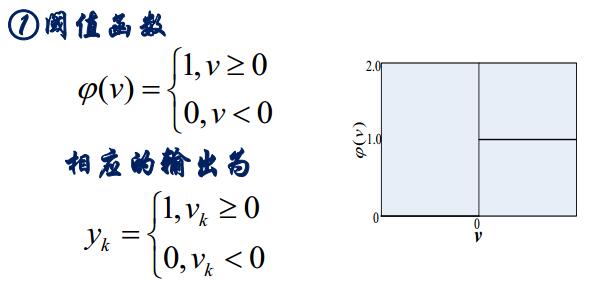
分段線性函式
例如
sigmoid函式

1.1.2網路的拓撲結構
前饋型網路:各神經元接收前一層的輸入並且輸出給下一層
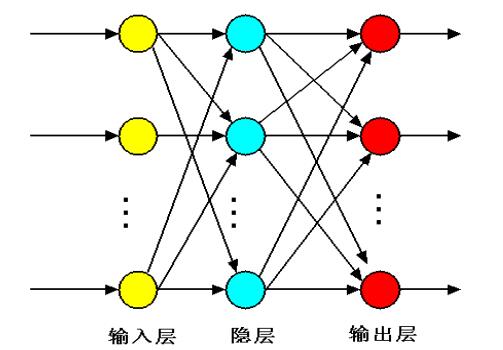
反饋型神經網路:
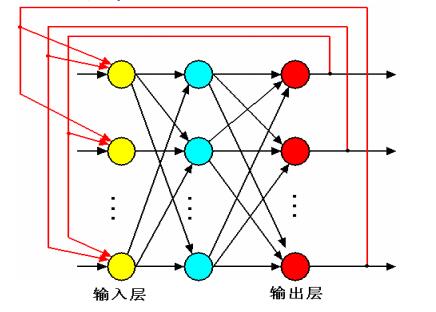
人工神經網路的工作過程
1、學習期:此時各個計算單元額狀態不變, 各連線線上的權值可以通過學習來修改(改變的是權值)
2、工作期:此時各個連線權固定,計算單元狀態的變化,以達到某種穩定狀態。(改變的輸出)
2.1感知器及其學習演算法
2.1.1線性閾值單元
線性閾值單元也叫做LTU,包括一個神經元和一組可調節的權值,神經元採用M-P模型(也就是啟用函式是閾值函式)
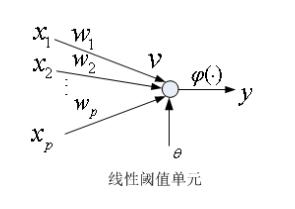
線性閾值單元可實現,與或非,與非等邏輯函式
異或邏輯是線性不可分的
2.1.2感知器
感知器是單層前饋神經網路,只有兩層,即輸入層和中間層
感知器只能解決線性可分問題,不 能解決異或問題
感知器的學習演算法:

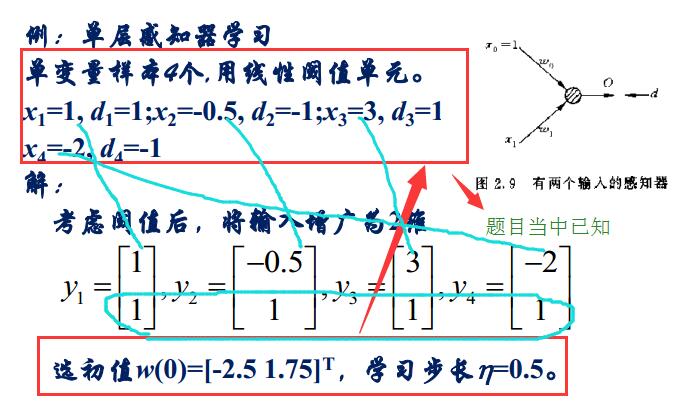
對於感知器的學習就是去求他的權值
然後再通過:
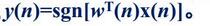
求出感知的輸出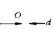
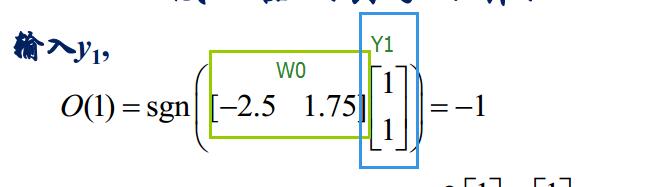
接下來要求調節權係數:
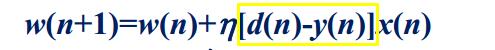
於是我們先求黃色框當中的式子,令e(n)=d(n)-y(n)(其中d(n)已知)
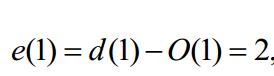
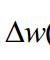
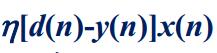
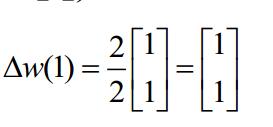
就可以求出下一秒的權值
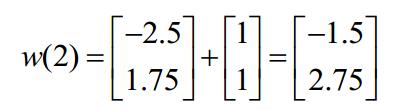

然後依次這樣求解下去
感知器的侷限性:
1、只能用來解決簡單問題
2、感知器僅能夠線性地將輸入的向量進行分類
3、當輸入的一個數據比另外一個數據大或者小的時候,可能收斂比較慢。
3.1多層前饋神經網路
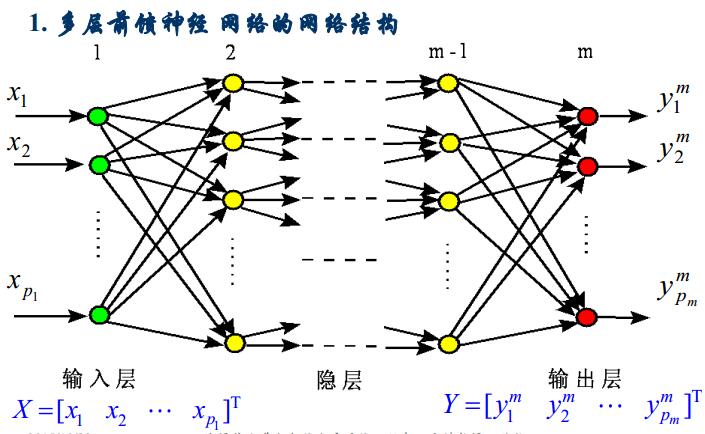
學習演算法:
正向傳播:輸入資訊由輸入層傳遞到隱層,最終在輸出層輸出。(改變的是輸出)
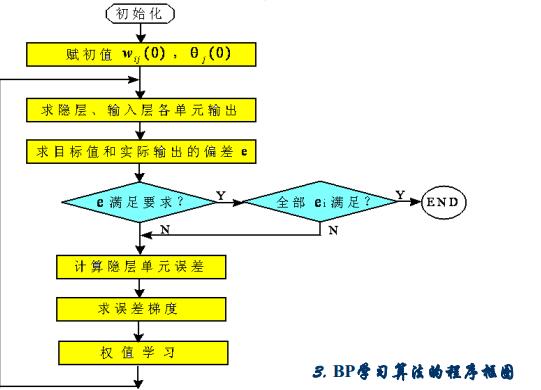
反向傳播:修改各層神經元之間的權值,使得誤差訊號最小.(改變的的權值)
BP神經網路也叫反向傳播學習演算法

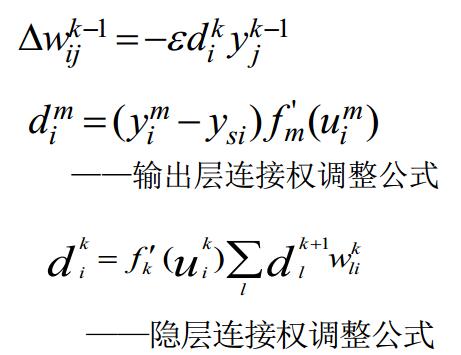
當啟用函式採用sigmoid函式的時候,上面的公式可以寫為:
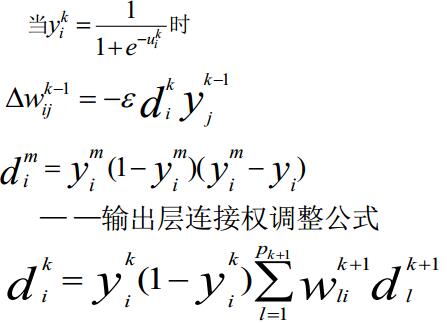
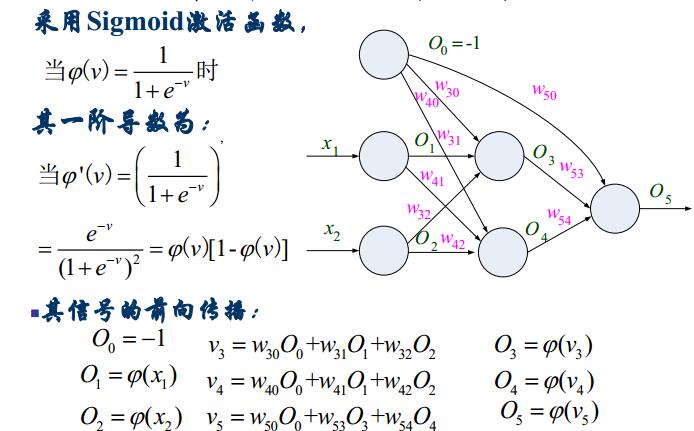
求輸出的正向的,求每個權值的誤差的反向的
BP的優點:
1、有很好的逼近
2、較強的泛化能力
3、較好的容錯性
存在的主要問題:
1、收斂速度慢
2、目標函式存在區域性極小點
3、難以確定隱層和隱層結點的數目
反向傳播學習演算法的一般步驟
1、初始化
選定合適的網路,設定所有可調節的引數(權值和閾值)
2、求連線權的權值和修正量
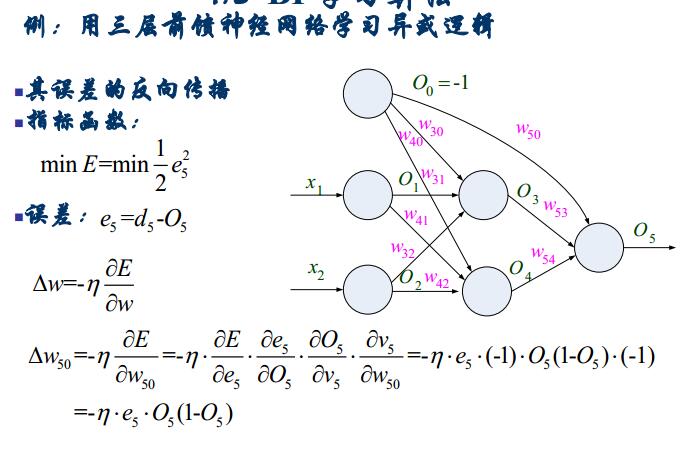

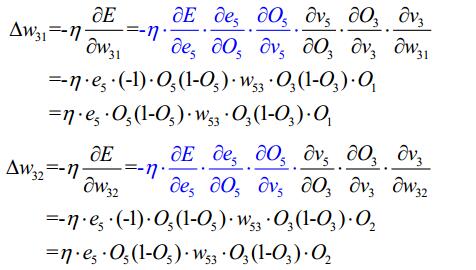
3.2BP演算法的設計流程圖


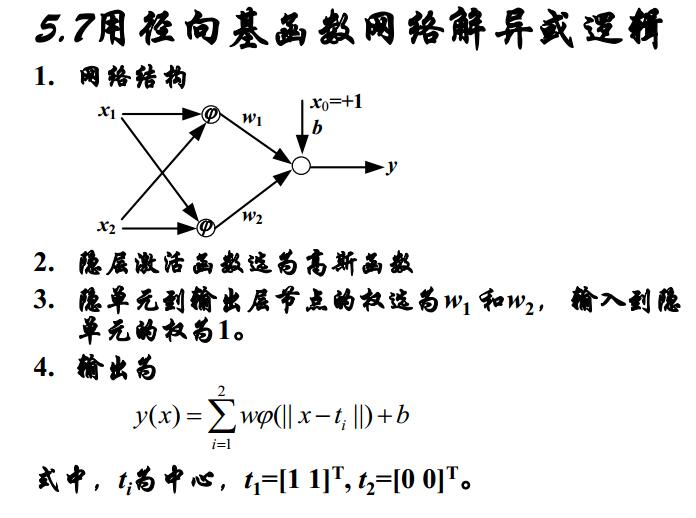
4.1徑向基函式
對於高維的數值分析,我們選擇一種空間和函式作為基底。一般而言,在處理多元函式的問題的基時候
選用:
徑向基函式 定義:
選擇N個基函式,每個基函式對應一個訓練資料,各基函式的形式為:
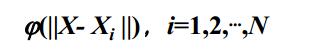
其中Xi是函式的中心,
最常用的徑向基函式是高斯核函式,高斯核函式的表示形式為:
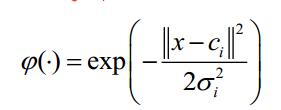
其中Ci 為核函式中心,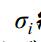
徑向基函式的網路一般包括三層,包含一個有輸入層,一個隱層和一個線性輸出層。隱層最常用的是高斯徑向基函式,而輸出層最常用的是線性啟用函式。RBF網路的權值訓練是一層一層進行的,對徑向基層的權值訓練可採用無導師訓練,在輸出層的權值設計可採用誤差糾正演算法,也就是有導師訓練
RBF的優點
RBF比多層前饋神經網路相比,規模大、但學習速度快、函式逼近、模式識別和分類能力都優於BP網路。
RBF神經元模型
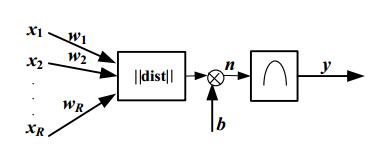
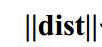
高斯函式表示式為:
RBF網路有三組可調引數:隱含層基函式中心、方差和隱含層單元到輸出單元的權值。
如何確定這三個引數,主要是有兩個方法:
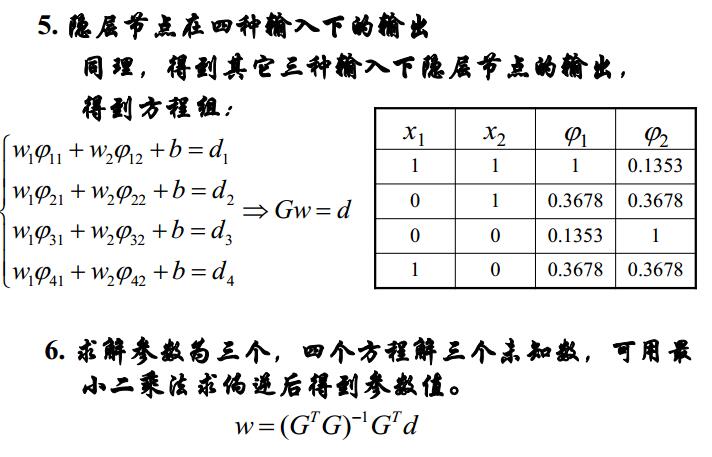
1、根據經驗和聚類方法選擇中心和方差,當選定中心和方差後,由於輸出是線性單元,他的權值可以採用迭代的最小二乘法直接計算出來。
2、通過訓練樣本,用誤差糾正演算法進行監督學習,逐步修正以上3個引數,也就是計算總的輸出誤差對各引數的梯度。再用梯度下降法修正待學習的引數。
一種採用K均值的聚類演算法確定各基函式的額中心,以及其方差,用區域性梯度下降法修正網路權值的演算法如下:


廣義RBF網路(GRNN)
Cover定理:將複雜的模式分類問題非線性地投射到高維空間,將比投射到低維空間更可能是線性可分的。
在RBF網路中,將輸入空間的模式(點)非線性地對映到一個高維空間的方式是:
設定一個隱層,令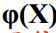
如果M足夠大,則在隱層空間輸入時線性可分的。
廣義RBF網路(GRNN)
正規化RBF網路的隱層結點個數和輸入樣本個數相等,但是樣本很大。
為了解決計算量很大的現象:
解決的方式:減少隱節點的個數,使得N<M<P
GRNN的基本思想:用徑向基函式做為隱單元的”基”,構成隱含層空間。隱含層對輸入向量進行變換,將低維空間的模式變換到高維空間內,使得低維空間內地線性不可分問題在高維空間內變得線性可分。
GRNN相比於RBF的特點:
1、M不等於N(M是隱層結點,N是輸入節點)常遠小於P(P是樣本個數)
2、徑向基函式的中心不再限制在資料點上,由訓練演算法確定
3、擴充套件常數不再統一,由訓練演算法確定
4、輸出函式的線性中包括閾值引數,以補償樣本的平均值與目標平均值間的差別
5、GRNN多用於函式逼近問題。
概率神經網路(PNN)
特點:1、網路隱層神經元的個數Q等於輸入向量樣本個數;輸出神經元的個數等於訓練樣本拘束的種類個數(k)
2、輸出層是競爭層,每個神經元對應於一類。
這種網路得到的分類結果能達到最大的正確概率。用於解決分類問題,當樣本足夠多的時候,收斂於一個貝葉斯分類器。
如何求一個矩陣和一個向量的範數
1、向量範數
2、矩陣範數



經驗風險最小化和結構風險最小化
對於未知的概率分佈,最小化風險函式,只有樣本資訊可以利用,這導致了定義的預測期望風險是無法直接計算和最小化的。
經驗風險最小化原則(ERM)原則:使用對引數W求經驗風險R的最小值 來 代替求期望風險Rw的最小值。
統計學習理論的核心內容
是小樣本統計估計和預測學習的基本理論,從理論上系統地研究了經驗風險最小化原則的條件,有限樣本條件下,經驗風險與期望風險的關係,以及如何應用改理論找到新的學習原則與方法等問題。
核心內容:
1、在經驗風險最小話的原則下、統計學習的一致性條件
2、在這些條件下關於統計學習推廣性的界的結論
3、在這些界的基礎上,建立小樣本歸納和推理原理
4、實現這些新的原則的實際演算法
學習理論的關鍵定理
如果損失函式有界,則經驗風險最小化學習一致的充要條件是
無免費午餐定理
不存在使適用於任何條件下的好方法,如果用推廣能力來衡量方法的好壞,對人和演算法,如果沒有限制條件,其效果不會好於隨機猜。
醜小鴨定理
如果不給出分類的目的,則世界上所有事物的相似程度是一樣的。
神經網路的構造過程
先確定網路的結構:網路的層數、每層節點數,相當於VC維的確定和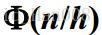
通過訓練確定最優權值,相當於最小化
結構風險最小化(SRM)
SVM支援向量機就是在結構風險最小化上應用的
總結(推廣能力,模型複雜度和樣本量)
在有限樣本的前提下:
1、經驗風險最小,並不一定意味期望風險最小
2、機器學習的複雜性不但與所研究的系統有關,而且要和有限的學習樣本想適應
3、用模型所含引數的多少作為模型複雜度的度量,這有的時候是不合理的
4、學習精度(深度)和推廣能力似乎是一種不可調和的矛盾,採用複雜的機器學習使得誤差很小,但是往往會喪失推廣能力。
推廣能力(泛化能力):機器對未來輸出進行正確的預測的能力
在某些情況下,訓練的誤差過小,反而會導致推廣能力下降(這就是過學習問題)
神經網路的過學習問題就是經驗風險最小化準則失敗的一個典型例子






Hopfield神經網路
聯想儲存器
記憶(儲存)是生物系統一個獨特而重要的功能;聯想儲存器(AM)是人腦記憶的一個重要形式
聯想記憶有兩個突出的特點:1、資訊的存取是通過資訊本身的額內容實驗的
2、資訊是分佈儲存的
離散型Hopfield神經網路


離散型Hopfield神經網路
穩定性定義:
若從某一時刻開始,網路中所有的神經元的狀態不再發生改變,則稱改網路是穩定的。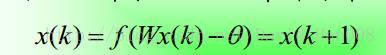
Hopfield神經網路是高維非線性系統,有許多個穩態。從任何初始狀態開始運動,總可以到某個穩定狀態,這些穩定的可以通過改變網路引數得到
穩定性定理:
序列穩定性–W:對稱且對角元素非負
並行穩定性–W:對稱,則總要收斂到一個穩定點或者是一個長度為2的震盪環
W:反對稱且對角元素為0,在一定條件下,網路將收斂於一個長度為4的環


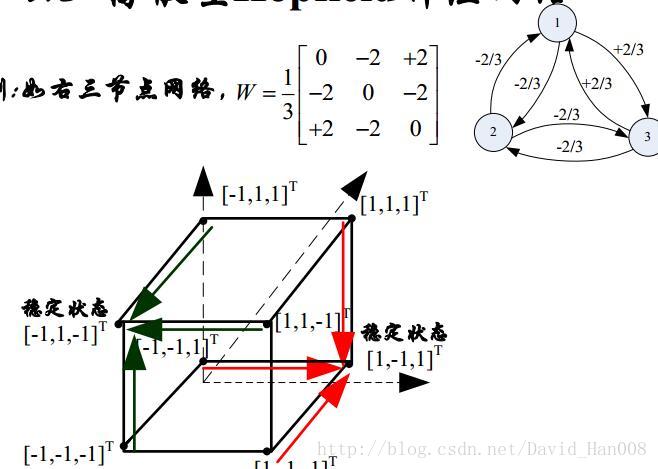
聯想儲存器的兩個性質:

隨機神經網路(模擬退火演算法)
模擬退火演算法(SA)

模擬退火演算法最大的貢獻在於,能以較大的概率求解複雜優化問題的全域性解。SA演算法可以分解為解空間,目標函式和初始解三部分。
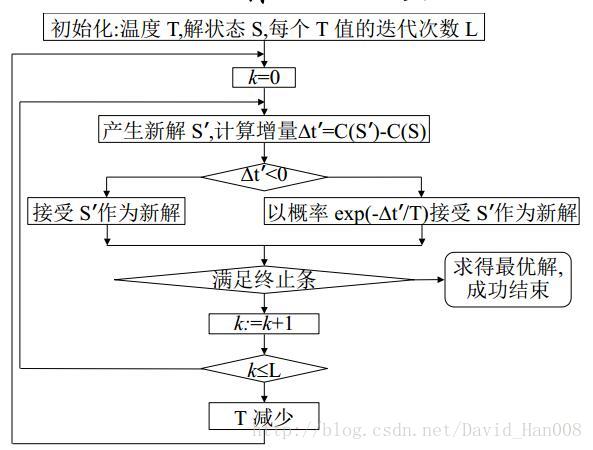




狀態接受函式的引入是SA演算法實現全域性搜尋的最關鍵因素

模擬退火演算法的優勢;

模擬退火演算法的不足:

SA演算法引數的控制問題


自組織系統 Hebb學習
自組織是指:其特定的結構和功能形成的,不是按照某種指令來完成的,而是由於系統內部要素彼此之間具有協調,相干或自發的默契行為,那麼這種形式特定結構與功能的過程就是自組織。

競爭:競爭就是系統間或系統內個要素或各子系統間相互競爭,力圖取得支配和主導地位的活動
協同:是指的系統中許多系統的聯合作用,各要素之間或各子系統之間在演化過程中存在著聯接,合作,協調和同步行為
自組織學習的必要前提:
只有當輸入資料中存在冗餘性時,非監督學習才得以進行,如果沒有這種冗餘性,非監督學習也無法發現數據中的重要特徵或者模式。從這個意義上可以理解為:冗餘性提供了知識。這種知識是自組織學習的必要前提。
主成分分析
主成分分析是一種通過降維技術吧多個變數化為少數幾個主成分的統計分析方法。這些主成分能夠反映原始變數的絕大部分資訊。他們通常表示為原始變數的某種線性組合。
主成分分析的一般目的:1、變數降維。2、主成分的解釋
主成分分析的計算例子:

競爭學習
競爭學習:網路的輸出神經元之間相互競爭以求彼此啟用,結果在每一時刻只有一個輸出神經元啟用。這個被啟用的神經元稱為競爭獲勝神經元,而其他神經元被抑制,稱為Winner Talk All.

自組織對映神經網路(SOM)
SOM網共有2層,輸入層模擬感知外界輸入資訊的視網膜,輸出層模擬做出相應的大腦皮層
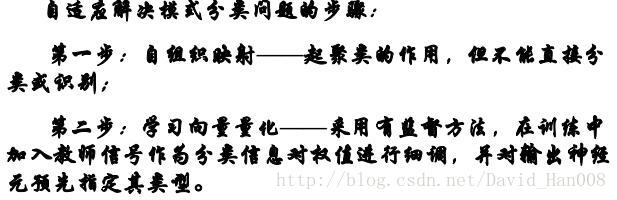
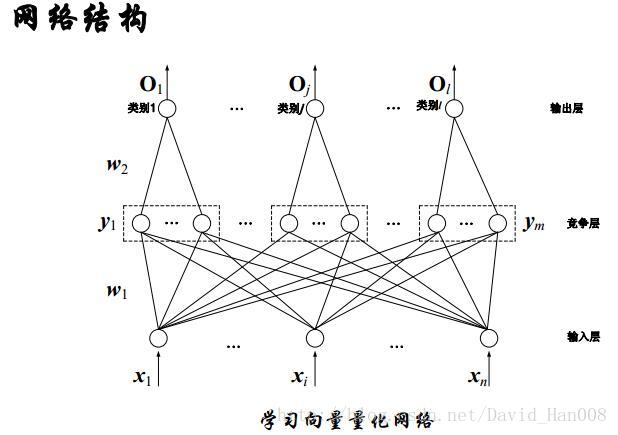
學習向量量化網路(LVQ)
向量量化(VO)是標量量化的擴充套件。他是把高維的資料離散化,鄰近的區域作為同一量化等級,用其中心來代表。這種演算法類似於逐次聚類演算法,聚類中心是該類的代表,(中心稱之為碼本)。
組成:輸入層神經元、競爭層神經元和輸出層神經元。
自適應共振理論(ART)
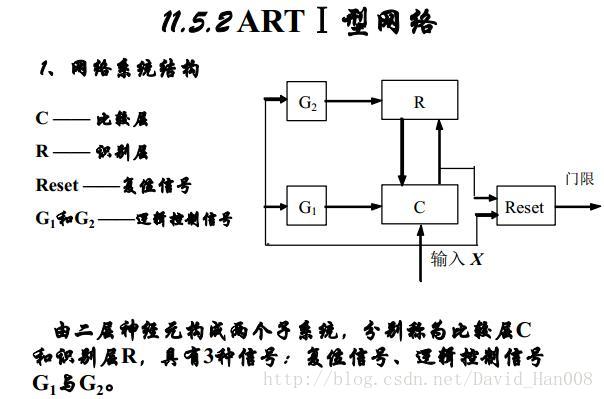

SOM網的結構特點是:輸出層神經元可排列成線陣或者面陣
LVQ網路是對SVO網路所獲得的聚類中心加以監督學習,以提高識別率。
貝葉斯網路以及其學習演算法

貝葉斯分類器是用於分類的貝葉斯網路,改網路中通常包括類節點和一組節點
模糊神經網路

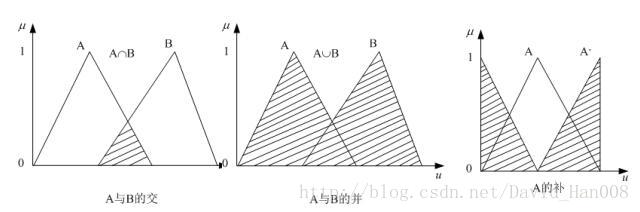

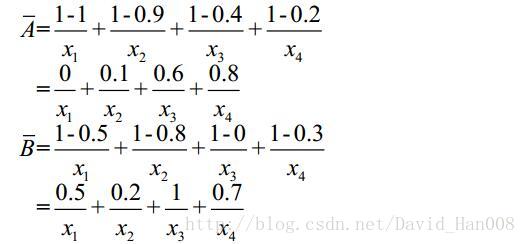



對映關係取最大值
模糊關係的合成運算

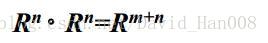
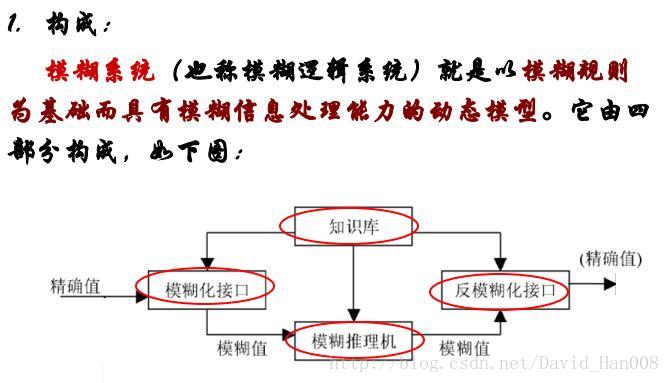
模糊系統和神經網路的區別與聯絡
1、模糊系統和神經網路都是計算智慧和計算方法
2、從知識的表達方式來看
模糊系統可以表達人的經驗性知識,便於理解
3、從知識的儲存方式來看
模糊系統將知識存在規則集中
神經網路將知識存在權係數當中,具有分佈儲存的特點
4、從知識的運用方式來看
模糊系統和神經網路都具有並行處理的特點
模糊神經網路同時被啟用的規則不多,計算量小
神經網路涉及的神經元很多,計算量大
5、從知識的獲取方式來看
模糊系統的規則靠專家提供和設計,難於自動獲取
神經網路的圈係數可由輸入輸出樣本中學習,無需人來設定
模糊神經網路FNN
核方法與支援向量機
核函式的作用:平滑(低通濾波)相似性度量

進化計算

遺傳演算法(GA)



遺傳演算法包括三個基本操作:選擇,交叉和變異


遺傳演算法五個基本要素:
1、引數編碼
2、初始群體的設定
3、適應度函式的設計
4、遺傳操作設計
5、控制引數設定
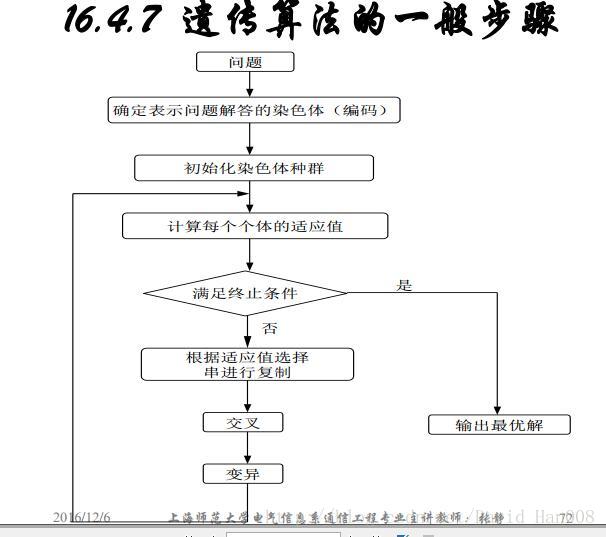

遺傳演算法的改進演算法
1、雙倍體遺傳演算法
2、雙種群遺傳演算法
3、自適應遺傳演算法