卷積神經網路學習筆記——Siamese networks（孿生神經網路）
完整程式碼及其資料，請移步小編的GitHub地址
傳送門：請點選我
如果點選有誤：https://github.com/LeBron-Jian/DeepLearningNote
在整理這些知識點之前，我建議先看一下原論文，不然看我這個筆記，感覺想到哪裡說哪裡，如果看了論文，還有不懂的，正好這篇部落格就是其詳細解析，包括原始碼解析。
我翻譯的連結：
深度學習論文翻譯解析（五）：Siamese Neural Networks for One-shot Image Recognition
下面開始：
1，Siamese Network 名字的由來
（名字的由來參考部落格：https://www.jianshu.com/p/92d7f6eaacf5）
Siamese和Chinese有點像。Siam是古時候泰國的稱呼，中文譯作暹羅（xianluo）。Siamese也就是“暹羅”人或“泰國”人。Siamese在英語中是“孿生”、“連體”的意思，這是為什麼呢？
十九世紀泰國出生了一對連體嬰兒，當時的醫學技術無法使兩人分離出來，於是兩人頑強地生活了一生，1829年被英國商人發現，進入馬戲團，在全世界各地表演，1839年他們訪問美國北卡羅萊那州後來成為“玲玲馬戲團” 的臺柱，最後成為美國公民。1843年4月13日跟英國一對姐妹結婚，恩生了10個小孩，昌生了12個，姐妹吵架時，兄弟就要輪流到每個老婆家住三天。1874年恩因肺病去世，另一位不久也去世，兩人均於63歲離開人間。兩人的肝至今仍儲存在費城的馬特博物館內。從此之後“暹羅雙胞胎”（Siamese twins）就成了連體人的代名詞，也因為這對雙胞胎讓全世界都重視到這項特殊疾病。
回到孿生網路，簡單來說，Siamese Network 就是“連體的神經網路”，神經網路的“連體”是通過共享權值來實現的。如下圖：
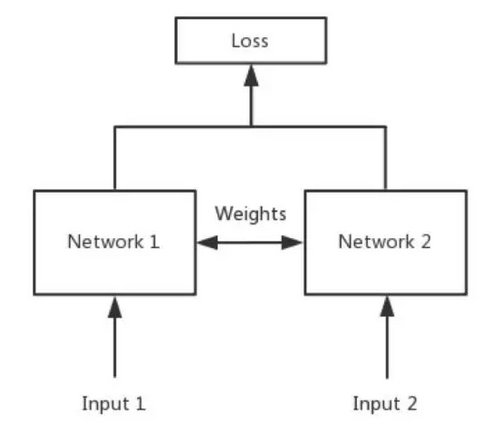
孿生網路是一種特殊型別的神經網路架構。與一個學習對其輸入進行分類的模型不同，該神經網路是學習在兩個輸入中進行區分。它學習了兩個輸入之間的相似之處。
當我們在做單樣本分類任務的時候，網路可以比較測試集與訓練集中的每張圖片，然後挑選出哪一張與他最可能是同樣類別。所以我們想讓神經網路架構同時輸入兩張圖片，輸出他們屬於同一個類別的概率。
假設 x1 和 x2是資料集中的兩個類別，我們讓 x1•x2 表示 x1 和 x2 是同一個類別。注意 x1•x2 與 x2•x1 是等價的——這意味著如果我們顛倒輸入圖片的順序，輸出的概率是完全相等的——p( x1•x2 ) 與 p( x2•x1 ) 相等。這被稱為對稱性，孿生網路就是依賴他設計的。
對稱性是非常重要的，因為他要學習一個距離度量——x1到 x2 的距離應該等於 x2 到 x1的距離。
如果我們僅僅把兩個樣本拼接起來，把它作為神經網路的單一的輸入，每個樣本將會是與一個不同權重集合的矩陣相乘（或纏繞），這會打破對稱性。沒問題，這樣子網路依然能成功的為每個輸入學習到完全相對的權重，但是對兩個輸入學習相等的權重集合會更容易一些。所以我們可以讓兩個輸入通過完全相對共享引數的網路，然後使用絕對差分作為線性分類器的輸入——這是孿生網路必須的結構。兩個完全相等的雙胞胎，共用一個頭顱，這就是孿生網路的由來。感覺放這個圖再切實不過了。
2，孿生神經網路的疑問及用途
孿生神經網路是一類包含兩個或更多個相同子網路的神經網路架構。這裡相同是指他們具有相同的配置即相同的引數和權重。引數更新在兩個子網上共同進行。
孿生神經網路在涉及發現相似性或兩個可比較的事物之間的關係的任務中留下。一些例子是複述評分，其中輸入是兩個句子，輸出是他們是多麼相似的得分；或者簽名驗證，確定兩個簽名是否來自同一個人。通常，在這樣的任務中，使用兩個相同的子網路來處理兩個輸入，並且另一個模型將取得他們的輸出併產生最終輸出。
2.1，共享權值是什麼？左右兩個神經網路的權重一模一樣嗎？
答：是的，在程式碼實現的時候，甚至可以是同一個網路，不用實現另外一個，因為權值都一樣。對於Siamase network，兩邊可以是lstm或者 cnn，都可以。
2.2，如果左右兩邊不共享權值，而是兩個不同的神經網路，叫什麼呢？
答：pseudo-siamese network，偽孿生神經網路，如下圖所示，對於pseudo-siamese network ，兩邊可以是不同的神經網路（如一個是 lstm，一個是cnn）也可以是相同型別的神經網路。
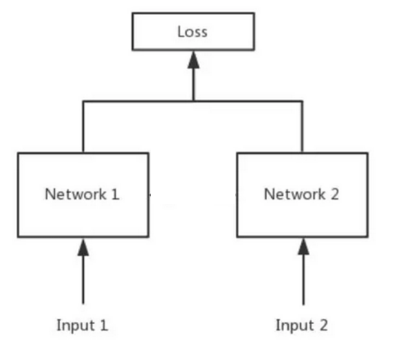
2.3，孿生神經網路的用途是什麼呢？
簡單來說，衡量兩個輸入的相似程度。孿生神經網路有兩個輸入（Input1 and input2），將兩個輸入 feed 進入兩個神經網路（Network1 and Network2），這兩個神經網路分別將輸入對映到新的空間，形成輸入在新的空間中的表示。通過Loss的計算，評價兩個輸入的相似度。
據知乎作者查到的資料，養樂村同志在NIPS 1993上發表了論文《Signature Verification using a ‘Siamese’ Time Delay Neural Network》用於美國支票上的簽名驗證，即驗證支票上的簽名與銀行預留簽名是否一致。1993年，養樂村同志就在用兩個卷積神經網路做簽名驗證了。 下面的圖片來自於Bromley et al (1993)[1]，他們為簽名驗證任務提出了一個孿生體系結構。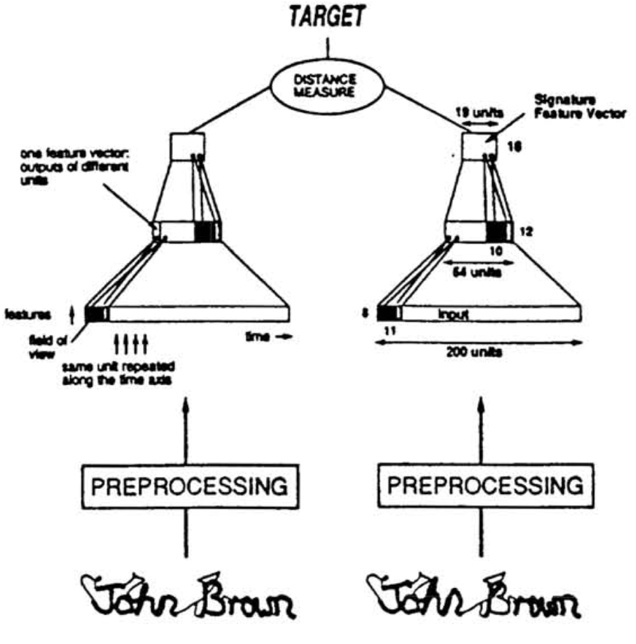
又比如在人臉領域，輸入兩個人的人臉圖片資訊，兩個網路分別提取這兩個人臉圖片中不同的部分。在圖中的網路，左右兩個網路的作用是用於提取輸入圖片的特徵。即特徵提取器
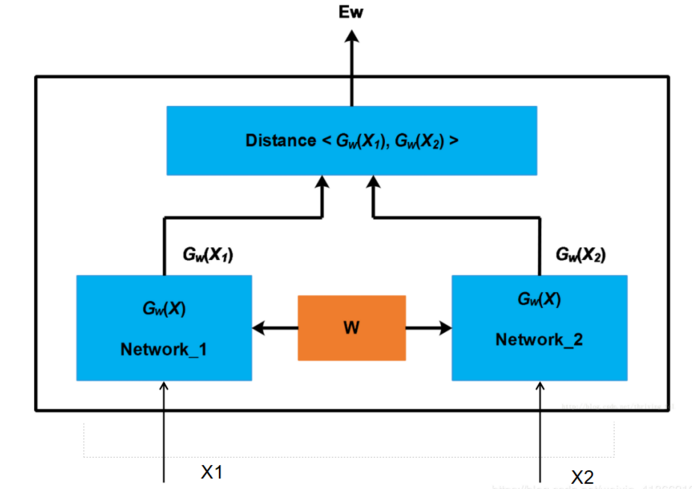
我們通過使用兩個網路提取出來了兩個圖片的特徵，然後我們需要計算特徵之間的差距distance，之後返回網路的輸出結果，看兩張圖片是否屬於同一個人。
2.4，孿生神經網路和偽孿生神經網路分別適用於什麼場景呢？
孿生神經網路用於處理兩個輸入“比較類似”的情況。偽孿生神經網路適用於處理兩個輸入“有一定差別”的情況。比如，我們要計算兩個句子或者詞彙的語義相似度，使用 Siamese Network 比較適合；如果驗證標題與正文描述是否一致（標題和正文長度差別很大），或者文字是否描述了一幅圖片（一個是圖片，一個是文字），就應該使用 pseudo-siamese network。也就是說要根據具體的應用，判斷應該使用哪一種結構，哪一種Loss。
2.5，Siamese Network loss function 一般用哪一種呢？
Softmax 當然是一種好的選擇，但是不一定是最優選擇，即使在分類問題中。傳統的Siamese Network使用Contrastive Loss。損失函式還有更多的選擇，Siamese Network的初衷是計算兩個輸入的相似度,。左右兩個神經網路分別將輸入轉換成一個"向量"，在新的空間中，通過判斷cosine距離就能得到相似度了。Cosine是一個選擇，exp function也是一種選擇，歐式距離什麼的都可以，訓練的目標是讓兩個相似的輸入距離儘可能的小，兩個不同類別的輸入距離儘可能的大。其他的距離度量沒有太多經驗，這裡簡單說一下cosine和exp在NLP中的區別。
根據實驗分析，cosine更適用於詞彙級別的語義相似度度量，而exp更適用於句子級別、段落級別的文字相似性度量。其中的原因可能是cosine僅僅計算兩個向量的夾角，exp還能夠儲存兩個向量的長度資訊，而句子蘊含更多的資訊。
2.6，Siamese Network是雙胞胎連體，整一個三胞胎連體可以不？
這個問題其實已經有人做過了，叫Triplet Network，論文是《Deep metric learning using Triplet network》，輸入是三個，一個正例 + 兩個負例，或者一個負例 + 兩個正例，訓練的目的是讓相同類別間的距離儘可能的小，讓不同類別間的距離儘可能的大。Triplet 在cifar，mnist的資料集上，效果都是很不錯的，超過了Siamese Network。
Triplet Network 圖如下：
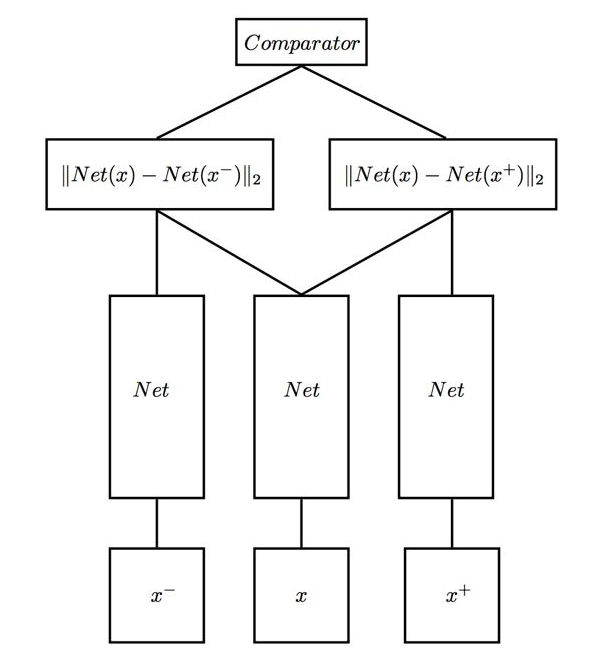
2.7，Siamese Network 的用途有哪些？
這個可以說太多了，nlp&cv領域都有很多應用。
- 前面提到的詞彙的語義相似度分析，QA中question和answer的匹配，簽名/人臉驗證。
- 手寫體識別也可以用siamese network，網上已有github程式碼。
- 還有kaggle上Quora的question pair的比賽，即判斷兩個提問是不是同一問題，冠軍隊伍用的就是n多特徵+Siamese network。
- 在影象上，基於Siamese網路的視覺跟蹤演算法也已經成為熱點《Fully-convolutional siamese networks for object tracking》。
3，Siamese Network 概述
Siamese Network 是一種神經網路的架構，而不是具體的某種網路，就像Seq2Seq一樣，具體實現上可以使用RNN也可以使用CNN。
Siamese Network 就像“連體的神經網路”，神經網路的“連體”是通過共享權值來實現的（共享權值即左右兩個神經網路的權重一模一樣）
Siamese Network的作用就是衡量兩個輸入的相似程度。孿生神經網路有兩個輸入（input1 and input2），將兩個輸入 feed 進入兩個神經網路（Network1 andNetwork2），這兩個神經網路分別將對映到新的空間，形成輸入在新的空間中的表示。通過Loss的計算，評價兩個輸入的相似度。
Siamese Network和其他網路的不同之處就在於，首先他是兩個輸入，他輸入的不是標籤，而是是否是同一類別，如果是同一類別就是0，否則就是1。
4，Contrastive Loss 損失函式
孿生架構的目的不是對輸入影象進行分類，而是區分它們。因此，分類損失函式（如交叉熵）不是最合適的選擇。相反，這種架構更適合使用對比函式。根據直覺而言，這個函式只是評估網路區分一對給定的影象的效果如何。
在傳統的孿生神經網路（Siamese Network）中，其採用的損失函式時Contrastive Loss，這種損失函式可以有效的處理孿生神經網路中的 paired data的關係。contrastive loss 的表示式如下：
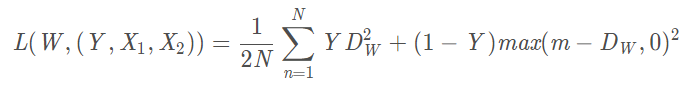
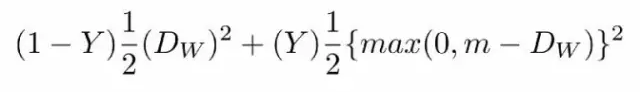
其中：
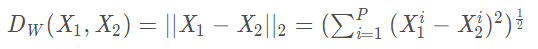
Dw被定義為孿生網路的輸出之間的歐式距離，代表兩個樣本特徵 X1 和 X2 的歐式距離（二範數）P表示樣本的特徵維數，Y表示兩個樣本是否匹配的標籤，Y=1代表兩個樣本相似或者匹配，Y=0代表不匹配，m即margin為設定的閾值。
所以對於孿生神經網路而言，當輸入的是同一張圖片的時候，我們希望他們之間的歐式距離很小，損失也越小；當不是同一張圖片的時候，歐式距離很大，損失也很大。簡單來說就是我們要最小化相同類的資料之間的距離，最大化不同類之間的距離。而觀察上述的 Contrastive Loss 的表示式可以發現，這種損失函式可以很好的表達成對樣本的匹配程度，也能夠很好地用於訓練提取特徵的模型。
當Y=1（即樣本相似時），損失函式只剩下：
即當樣本相似時，如果在特徵空間的歐式距離較大，則說明當前的模型不好，因此加大損失。
當Y=0（即樣本不相似時），損失函式為：
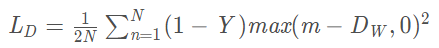
即當樣本不相似時，其特徵空間的歐式距離反而小的話，損失值會變大，這也正好符合我們的要求。
注意：這裡設定了一個閾值 margin，表示我們只考慮不相似特徵歐式距離在 0~margin之間的，當距離超過 margin的，則把其loss看做為 0 （即不相似的特徵離的很遠，其 loss 應該是很低的；而對於相似的特徵反而離的很遠，我們就需要增加其 loss， 從而不斷更新成對樣本的匹配程度）
下面這張圖就是損失函式值與樣本特徵的歐式距離之間的關係，其中紅線虛線表示的是相似樣本的損失值，藍色實現表示的是不相似樣本的損失值。
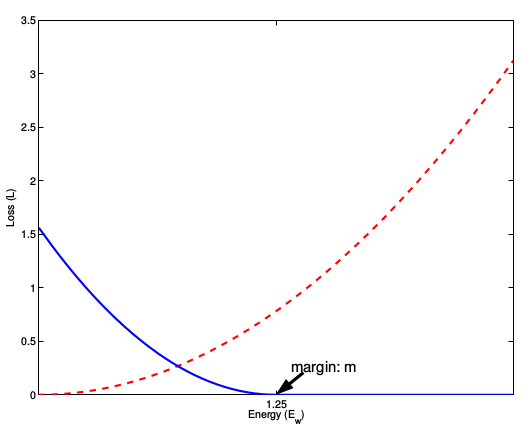
5，網路架構
Koch 等人使用卷積孿生網路去分類成對的Omniglot影象，所以這兩個孿生網路都是卷積神經網路。這兩個孿生網路每個的架構如下：64通道的10*10卷積核，relu -> max pool -> 128 通道的 7*7 卷積核， relu -> max pool -> 128 通道的 4*4 卷積核，relu -> max pool -> 256通道的 4*4 卷積核。孿生網路把輸入降低到越來越小的3d張量上，最終他們經過一個 4096 神經元的全連線層。兩個向量的絕對差作為線性分類器的輸入。這個網路一共有 38951745 個引數——96%的引數屬於全連線層。這個引數量很大，所以網路有很高的過擬合風險，但是成對的訓練意味著資料集是很大的，所以過擬合問題不曾出現。
輸出被歸一化到 [0, 1]之間，使用 Sigmoid函式讓它變成一個概率，當兩個影象是相同類別的時候，我們使目標 t=1，類別不相同的時候 t=0，它使用Logistic迴歸來訓練。這意味著損失函式應該是預測和目標之間的二分類交叉熵。損失函式中還有一個 L2 權重衰減項，以讓網路可以學習更小的\更平滑的權重，從而提高泛化能力：
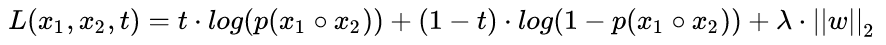
當網路做單樣本學習的時候，孿生網路簡單的分類一下測試影象與訓練集中的影象中那個最相似就可以了：
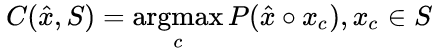
這裡使用argmax 而不是近鄰方法中的 argmin，因為類別越不同，L2度量的值越高，但是這個模型的輸出 p( x1•x2 ) ，所以我們要這個值最大。這個方法有一個明顯的缺陷：對於訓練集中的 Xa，概率 x1•x2 與訓練集中每個樣本都是獨立的！這意味著概率值的和不為1.言歸正傳，測試影象與訓練影象應該是相同型別的。。。
5.1逐對訓練的有效的資料集大小
作者注意到：採用逐對訓練的話，將會有平方級別對的影象對來訓練模型，這讓模型很難過擬合，很好。假設我們有 E 類，每類有 C 個樣本。一共有 C•E 張圖片，總共可能的配方數量可以這樣計算：
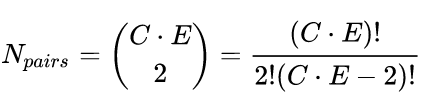
對於 omniglot 中的 964類（每類20個樣本），這會有 185849560 個可能的配對，這是巨大的！然而，孿生網路需要相同類的和不同類的配對都有。每類 E 個訓練樣本，所以每個類別有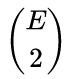 
對，這意味著有 
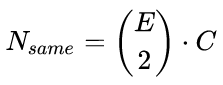個相同類別的配對。對於 Omniglot 有 183160對。即使 183160對已經很大了，但他只是所有可能配對的千分之一，因為相同類別的配對數量隨著 E平方級的增大，但是隨著C是線性增加。這個問題非常重要，因為孿生網路訓練的時候，同類別和不同類別的比例應該是1:1，或許它表明逐對訓練在那種每個類別有更多樣本的資料集上更容易訓練。
5.2 程式碼
下面是模型定義，如果你見過Keras，那很容易理解。這裡只用 Sequential() 來定義一次孿生網路，然後使用兩個輸入層來呼叫它，這樣兩個輸入使用相同的引數。然後我們把他們使用絕對距離合並起來，新增一個輸出層，使用二分類交叉熵損失來編譯這個模型。
# _*_coding:utf-8_*_
from keras.layers import Input, Conv2D, Lambda, merge, Dense, Flatten, MaxPooling2D
from keras.models import Model, Sequential
from keras.regularizers import l2
from keras import backend as K
from keras.optimizers import SGD, Adam
from keras.losses import binary_crossentropy
import numpy.random as rng
import numpy as np
import os
import dill as pickle
import matplotlib.pyplot as plt
from sklearn.utils import shuffle
import tensorflow as tf
def W_init(shape, name=None):
''' Initiallize weights as in paper'''
values = rng.normal(loc=0, scale=1e-2, size=shape)
return K.variable(values, name=name)
# //TODO figure out how to initialize layer biases in keras
def b_init(shape, name=None):
"""Initialize bias as in paper"""
values = rng.normal(loc=0.5, scale=1e-2, size=shape)
return K.variable(values, name=name)
input_shape = (105, 105, 1)
left_input = Input(input_shape)
right_input = Input(input_shape)
# build convnet to use in each siamese 'leg'
convnet = Sequential()
convnet.add(Conv2D(64, (10, 10), activation='relu', input_shape=input_shape,
kernel_initializer=W_init, kernel_regularizer=l2(2e-4)))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(128, (7, 7), activation='relu',
kernel_regularizer=l2(2e-4), kernel_initializer=W_init, bias_initializer=b_init))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(128, (4, 4), activation='relu', kernel_initializer=W_init, kernel_regularizer=l2(2e-4),
bias_initializer=b_init))
convnet.add(MaxPooling2D())
convnet.add(Conv2D(256, (4, 4), activation='relu', kernel_initializer=W_init, kernel_regularizer=l2(2e-4),
bias_initializer=b_init))
convnet.add(Flatten())
convnet.add(
Dense(4096, activation="sigmoid", kernel_regularizer=l2(1e-3), kernel_initializer=W_init, bias_initializer=b_init))
# encode each of the two inputs into a vector with the convnet
encoded_l = convnet(left_input)
encoded_r = convnet(right_input)
# merge two encoded inputs with the l1 distance between them
L1_distance = lambda x: K.abs(x[0] - x[1])
both = merge([encoded_l, encoded_r], mode=L1_distance, output_shape=lambda x: x[0])
prediction = Dense(1, activation='sigmoid', bias_initializer=b_init)(both)
siamese_net = Model(input=[left_input, right_input], output=prediction)
# optimizer = SGD(0.0004,momentum=0.6,nesterov=True,decay=0.0003)
optimizer = Adam(0.00006)
# //TODO: get layerwise learning rates and momentum annealing scheme described in paperworking
siamese_net.compile(loss="binary_crossentropy", optimizer=optimizer)
siamese_net.count_params()
原論文中每個層的學習率和衝量都不相同，因為使用Keras來實現這個太麻煩，並且超引數不是重點。Koch等人增加向訓練集中增加失真的影象，使用 150000 對樣本訓練模型。因為這個太大了，我的記憶體放下下，所以我決定使用隨機取樣的方法。載入影象對或許是這個模型最難實現的部分，因為這裡每個類別有20個樣本，我們把資料調整為 N_Classes*20*105*105 的陣列，這樣可以很方便的來索引。
class Siamese_Loader:
"""For loading batches and testing tasks to a siamese net"""
def __init__(self, Xtrain, Xval):
self.Xval = Xval
self.Xtrain = Xtrain
self.n_classes, self.n_examples, self.w, self.h = Xtrain.shape
self.n_val, self.n_ex_val, _, _ = Xval.shape
def get_batch(self, n):
"""Create batch of n pairs, half same class, half different class"""
categories = rng.choice(self.n_classes, size=(n,), replace=False)
pairs = [np.zeros((n, self.h, self.w, 1)) for i in range(2)]
targets = np.zeros((n,))
targets[n // 2:] = 1
for i in range(n):
category = categories[i]
idx_1 = rng.randint(0, self.n_examples)
pairs[0][i, :, :, :] = self.Xtrain[category, idx_1].reshape(self.w, self.h, 1)
idx_2 = rng.randint(0, self.n_examples)
# pick images of same class for 1st half, different for 2nd
category_2 = category if i >= n // 2 else (category + rng.randint(1, self.n_classes)) % self.n_classes
pairs[1][i, :, :, :] = self.Xtrain[category_2, idx_2].reshape(self.w, self.h, 1)
return pairs, targets
def make_oneshot_task(self, N):
"""Create pairs of test image, support set for testing N way one-shot learning. """
categories = rng.choice(self.n_val, size=(N,), replace=False)
indices = rng.randint(0, self.n_ex_val, size=(N,))
true_category = categories[0]
ex1, ex2 = rng.choice(self.n_examples, replace=False, size=(2,))
test_image = np.asarray([self.Xval[true_category, ex1, :, :]] * N).reshape(N, self.w, self.h, 1)
support_set = self.Xval[categories, indices, :, :]
support_set[0, :, :] = self.Xval[true_category, ex2]
support_set = support_set.reshape(N, self.w, self.h, 1)
pairs = [test_image, support_set]
targets = np.zeros((N,))
targets[0] = 1
return pairs, targets
def test_oneshot(self, model, N, k, verbose=0):
"""Test average N way oneshot learning accuracy of a siamese neural net over k one-shot tasks"""
pass
n_correct = 0
if verbose:
print("Evaluating model on {} unique {} way one-shot learning tasks ...".format(k, N))
for i in range(k):
inputs, targets = self.make_oneshot_task(N)
probs = model.predict(inputs)
if np.argmax(probs) == 0:
n_correct += 1
percent_correct = (100.0 * n_correct / k)
if verbose:
print("Got an average of {}% {} way one-shot learning accuracy".format(percent_correct, N))
return percent_correct
下面是訓練過程了。沒什麼特別的，除了我監測的時驗證機精度來測試效能，而不是驗證集上的損失。
evaluate_every = 7000
loss_every=300
batch_size = 32
N_way = 20
n_val = 550
siamese_net.load_weights("PATH")
best = 76.0
for i in range(900000):
(inputs,targets)=loader.get_batch(batch_size)
loss=siamese_net.train_on_batch(inputs,targets)
if i % evaluate_every == 0:
val_acc = loader.test_oneshot(siamese_net,N_way,n_val,verbose=True)
if val_acc >= best:
print("saving")
siamese_net.save('PATH')
best=val_acc
if i % loss_every == 0:
print("iteration {}, training loss: {:.2f},".format(i,loss))
5.3 結果
一旦學習曲線變平整了，我使用在20類驗證集合上表現最好的模型來測試。我的網路在驗證集上得到了大約83%的精度，原論文精度是93%，或許這個差別是因為我沒有實現原論文中的很多增強效能的技巧，像逐層的學習率/衝量，使用資料失真的資料增強方法，貝葉斯超引數優化，並且其迭代次數也不夠。但是沒關係，這個教程側重於簡要介紹單樣本的學習，而不是在其百分之幾的分類效能上鑽牛角尖。
5.4 討論
現在我們只是訓練了一個來做鑑別相同還是不同的二分類網路。更重要的是，我們展現了模型能夠在沒有見過的字母表上的20類單樣本學習的效能。當然，這不是使用深度學習來做單樣本學習的唯一方式。
正如前面提到的，孿生網路的最大缺陷是它要拿測試影象與訓練集中影象逐個比較。當這個網路將測試影象與任何影象 x1 相比，不管訓練集是什麼，P(xhat*x1) 都是相同的。這很愚蠢，假如你在做單樣本學習任務，你看到一張圖片與測試影象非常類似。然而，當你看到訓練中另外一張圖片也與測試集非常相似，你就會對他的類別沒有那麼自信了。訓練目標與測試目標是不同的，如果有一個模型可以很好地比較測試圖片與訓練集，並且使用僅僅有一個訓練圖片與之擁有相同類別的限制，那麼模型會表現的更好。
Matching Networks for One Shot learning這篇論文就是做這個的。它們使用深度模型來端到端的學習一個完整的近鄰分類器，而不是學習相似度函式，直接在單樣本任務上訓練，而不是在一個影象對上。Andrej Karpathy’s notes很好的解釋了這個問題。因為你正在學習機器分類，所以你可以把他視為元學習（meta learning）。One-shot Learning with Memory-Augmented Neural Networks 這篇論文解釋了單樣本學習與元學習的關係，它在omniglot資料集上訓練了一個記憶增強網路，然而，我承認我看不懂這篇論文。
6，Keras 實現Siamese Network
整理了這麼多，就是說自己想學習Siamese network ，但是網上目前找到的資源就這麼多，而且自己都整理出來了，大概也明白了其意義，瞭解了其損失函式，明白了網路架構原理。接下來就是練習的時刻了。
6.1 在MNIST資料集上訓練Siamese network
既然都會了，那麼就實踐一下，首先，我們用mnist 資料集做實踐，而這個的程式碼是keras官方給的，程式碼如下：
from __future__ import absolute_import
from __future__ import print_function
import numpy as np
import random
from keras.datasets import mnist
from keras.models import Model
from keras.layers import Input, Flatten, Dense, Dropout, Lambda
from keras.optimizers import RMSprop
from keras import backend as K
num_classes = 10
epochs = 20
def euclidean_distance(vects):
x, y = vects
sum_square = K.sum(K.square(x - y), axis=1, keepdims=True)
return K.sqrt(K.maximum(sum_square, K.epsilon()))
def eucl_dist_output_shape(shapes):
shape1, shape2 = shapes
return (shape1[0], 1)
def contrastive_loss(y_true, y_pred):
'''Contrastive loss from Hadsell-et-al.'06
http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
'''
margin = 1
square_pred = K.square(y_pred)
margin_square = K.square(K.maximum(margin - y_pred, 0))
return K.mean(y_true * square_pred + (1 - y_true) * margin_square)
def create_pairs(x, digit_indices):
'''Positive and negative pair creation.
Alternates between positive and negative pairs.
'''
pairs = []
labels = []
n = min([len(digit_indices[d]) for d in range(num_classes)]) - 1
for d in range(num_classes):
for i in range(n):
z1, z2 = digit_indices[d][i], digit_indices[d][i + 1]
pairs += [[x[z1], x[z2]]]
inc = random.randrange(1, num_classes)
dn = (d + inc) % num_classes
z1, z2 = digit_indices[d][i], digit_indices[dn][i]
pairs += [[x[z1], x[z2]]]
labels += [1, 0]
return np.array(pairs), np.array(labels)
def create_base_network(input_shape):
'''Base network to be shared (eq. to feature extraction).
'''
input = Input(shape=input_shape)
x = Flatten()(input)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
return Model(input, x)
def compute_accuracy(y_true, y_pred):
'''Compute classification accuracy with a fixed threshold on distances.
'''
pred = y_pred.ravel() < 0.5
return np.mean(pred == y_true)
def accuracy(y_true, y_pred):
'''Compute classification accuracy with a fixed threshold on distances.
'''
return K.mean(K.equal(y_true, K.cast(y_pred < 0.5, y_true.dtype)))
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
input_shape = x_train.shape[1:]
# create training+test positive and negative pairs
digit_indices = [np.where(y_train == i)[0] for i in range(num_classes)]
tr_pairs, tr_y = create_pairs(x_train, digit_indices)
digit_indices = [np.where(y_test == i)[0] for i in range(num_classes)]
te_pairs, te_y = create_pairs(x_test, digit_indices)
# network definition
base_network = create_base_network(input_shape)
input_a = Input(shape=input_shape)
input_b = Input(shape=input_shape)
# because we re-use the same instance `base_network`,
# the weights of the network
# will be shared across the two branches
processed_a = base_network(input_a)
processed_b = base_network(input_b)
distance = Lambda(euclidean_distance,
output_shape=eucl_dist_output_shape)([processed_a, processed_b])
model = Model([input_a, input_b], distance)
# train
rms = RMSprop()
model.compile(loss=contrastive_loss, optimizer=rms, metrics=[accuracy])
model.fit([tr_pairs[:, 0], tr_pairs[:, 1]], tr_y,
batch_size=128,
epochs=epochs,
validation_data=([te_pairs[:, 0], te_pairs[:, 1]], te_y))
# compute final accuracy on training and test sets
y_pred = model.predict([tr_pairs[:, 0], tr_pairs[:, 1]])
tr_acc = compute_accuracy(tr_y, y_pred)
y_pred = model.predict([te_pairs[:, 0], te_pairs[:, 1]])
te_acc = compute_accuracy(te_y, y_pred)
print('* Accuracy on training set: %0.2f%%' % (100 * tr_acc))
print('* Accuracy on test set: %0.2f%%' % (100 * te_acc))
結果如下：
106112/108400 [============================>.] - ETA: 0s - loss: 0.0101 - accuracy: 0.9903 107136/108400 [============================>.] - ETA: 0s - loss: 0.0100 - accuracy: 0.9903 108160/108400 [============================>.] - ETA: 0s - loss: 0.0101 - accuracy: 0.9903 108400/108400 [==============================] - 8s 75us/step - loss: 0.0101 - accuracy: 0.9903 - val_loss: 0.0263 - val_accuracy: 0.9730 * Accuracy on training set: 99.59% * Accuracy on test set: 97.30%
分析結果，我們可以知道在MNIST資料集中，我們成對的訓練Siamese Network，然後通過計算共享網路輸出上的歐幾里得距離，通過20個epochs 後，準確率達到了97.3%。
我們可以畫出損失圖，畫損失圖程式碼如下：
import matplotlib.pyplot as plt
def plot_training(history):
plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
train_acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
plt.plot(train_acc, '-o', label='train_acc')
plt.plot(val_acc, '-o', label='test_acc')
plt.xlabel('Epochs')
plt.legend()
plt.subplot(1, 2, 2)
train_acc = history.history['loss']
val_acc = history.history['val_loss']
plt.plot(train_acc, '-o', label='train_loss')
plt.plot(val_acc, '-o', label='test_loss')
plt.xlabel('Epochs')
plt.legend()
損失圖如下：
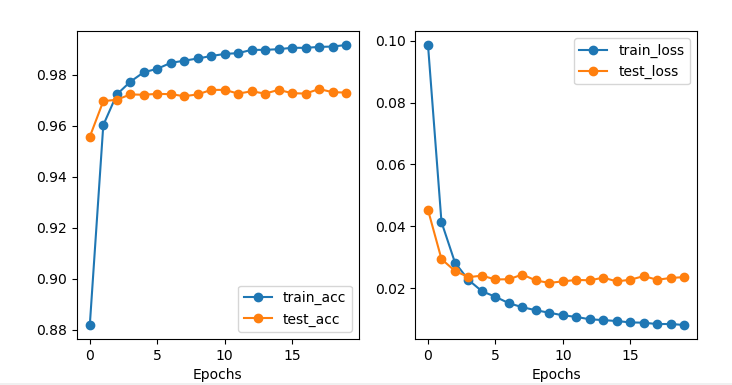
下面對上面程式碼進行分析。
其實程式碼比較簡單，Contrastive loss function 程式碼如下：
def contrastive_loss(y_true, y_pred):
'''Contrastive loss from Hadsell-et-al.'06
http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
'''
margin = 1
square_pred = K.square(y_pred)
margin_square = K.square(K.maximum(margin - y_pred, 0))
return K.mean(y_true * square_pred + (1 - y_true) * margin_square)
這是照著公式寫的，就不多說。
而此模型，我們仔細觀察，就是多層感知器，只不過是使用Keras的函式式完成的。
def create_base_network(input_shape):
'''Base network to be shared (eq. to feature extraction).
'''
input = Input(shape=input_shape)
x = Flatten()(input)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
return Model(input, x)
這個程式碼是一個三層的感知器，其實理解了程式碼之後，實現 n 層感知器都不是問題。所以只需要理解好這個三層的MLP模型即可。概況的說，MLP的輸入層X其實就是我們的訓練資料，而這裡的處理就是Flatten 。輸入層實現後，輸入層到隱含層就是一個全連線的層，利用Dense() 函式（此函式為Keras內建的全連線層函式）即可。
下面要說的就是他資料的輸入方式：
def create_pairs(x, digit_indices):
'''Positive and negative pair creation.
Alternates between positive and negative pairs.
'''
pairs = []
labels = []
n = min([len(digit_indices[d]) for d in range(num_classes)]) - 1
for d in range(num_classes):
for i in range(n):
z1, z2 = digit_indices[d][i], digit_indices[d][i + 1]
pairs += [[x[z1], x[z2]]]
inc = random.randrange(1, num_classes)
dn = (d + inc) % num_classes
z1, z2 = digit_indices[d][i], digit_indices[dn][i]
pairs += [[x[z1], x[z2]]]
labels += [1, 0]
return np.array(pairs), np.array(labels)
從程式碼中，我們可以看出，它將資料綁成一對一對的，將兩個同類的資料綁一起，用label 1表示；將兩個不同類的照片綁一起，用label 0表示。前面5.1提到過資料兩兩組合有很多種方式，大概有平方級別的影象對。這裡採用了一種巧妙的方法，就是將第n張圖片與n+1張相同的照片綁一起，這樣一來就避免了大量的影象對了。而且這種方式我們的影象是不需要標籤的。我們的標籤是函式裡面設定好的，這個和傳統的分類演算法也是有區別的，簡單來說就是這裡輸入的不是標籤，而是是否是同一類別。
這裡強調一下，使用影象對訓練模型，這樣模型就很難過擬合。
最後就是喂入資料，進行訓練了，訓練就不說了，和傳統的分類是一樣的。但是喂入資料還是不同的，是Siamese Network特有的方式，程式碼如下：
# network definition
base_network = create_base_network(input_shape)
input_a = Input(shape=input_shape)
input_b = Input(shape=input_shape)
processed_a = base_network(input_a)
processed_b = base_network(input_b)
distance = Lambda(euclidean_distance,
output_shape=eucl_dist_output_shape)([processed_a, processed_b])
model = Model([input_a, input_b], distance)
我們也看到過，上面只使用函式定義了一次網路，然後這裡使用兩個輸入層（input_a, input_b）來呼叫它，這樣兩個輸入使用相同的引數，然後feed進入相同的神經網路，這兩個神經網路分別對映到新的空間（processed_a, processed_b）。然後我們需要將他們使用絕對距離合並起來，新增一個輸出層（distance），最後使用二分類交叉熵來編譯這個模型。
總體來說，使用Keras實現的話，程式碼簡單，易於理解。
6.2 在自己的資料集上訓練Siamese network
既然可以在MNIST的資料集訓練資料，那麼也可以在自己的資料集訓練。這裡我採用的資料集是五分類。
資料描述：
共有500張圖片，分為大巴車、恐龍、大象、鮮花和馬五個類，每個類100張。下載地址：http://pan.baidu.com/s/1nuqlTnN
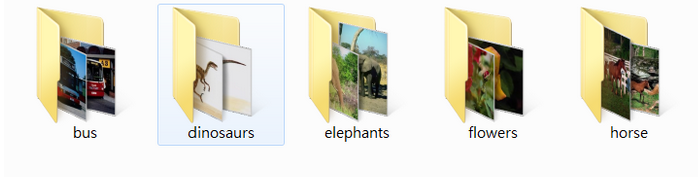
我們先匯入資料：
def get_image_data(imagePaths, label):
data = []
labels = []
for image_name in os.listdir(imagePaths):
imagePath = os.path.join(imagePaths, image_name)
image = cv2.imread(imagePath)
image = cv2.resize(image, target_size)
data.append(image)
labels.append(label)
data = np.array(data, dtype='float')
data /= 255.0
labels = np.array(labels)
data, labels = shuffle(data, labels, random_state=0)
return data, labels
def load_train_test_data():
filelist = []
for i in os.listdir(file_path):
filelist.append(i)
data = []
labels = []
for i in range(len(filelist)):
filedir = filelist[i]
allpath = os.path.join(file_path, filelist[i])
data_i, labels_i = get_image_data(imagePaths=allpath, label=filedir)
data_i, labels_i = list(data_i), list(labels_i)
data.extend(data_i)
labels.extend(labels_i)
data, labels = np.array(data), np.array(labels)
x_train, x_test, y_train, y_test = train_test_split(data, labels, test_size=0.2, random_state=123456)
return x_train, x_test, y_train, y_test, filelist
def load_data():
x_train, x_test, y_train, y_test, filelist = load_train_test_data()
print(x_train.shape, y_train.shape)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
# x_train /= 255.0
# x_test /= 255.0
input_shape = x_train.shape[1:] # (80, 80)
digit_indices = [np.where(y_train == filelist[i])[0] for i in range(num_classes)]
tr_pairs, tr_y = create_pairs(x_train, digit_indices)
digit_indices = [np.where(y_test == filelist[i])[0] for i in range(num_classes)]
te_pairs, te_y = create_pairs(x_test, digit_indices)
# print(te_pairs.shape, te_y.shape) # (980, 2, 80, 80) (980,)
return input_shape, tr_pairs, tr_y, te_pairs, te_y
然後我們使用MLP模型訓練：
def create_base_network(input_shape):
'''Base network to be shared (eq. to feature extraction).'''
input = Input(shape=input_shape)
x = Flatten()(input)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
x = Dropout(0.1)(x)
x = Dense(128, activation='relu')(x)
return Model(input, x)
其他與上面類似，這裡不重複貼了。結果如下：
- 2s - loss: 14.9671 - accuracy: 0.5171 - val_loss: 0.2103 - val_accuracy: 0.6643 Epoch 2/100 - 0s - loss: 0.2774 - accuracy: 0.5684 - val_loss: 0.2842 - val_accuracy: 0.5071 Epoch 3/100 - 0s - loss: 0.2781 - accuracy: 0.5776 - val_loss: 0.1577 - val_accuracy: 0.7643 Epoch 4/100 - 0s - loss: 0.4256 - accuracy: 0.5224 - val_loss: 0.1693 - val_accuracy: 0.7857 Epoch 5/100 - 0s - loss: 0.4215 - accuracy: 0.5224 - val_loss: 0.2731 - val_accuracy: 0.5214 Epoch 6/100 - 0s - loss: 0.4870 - accuracy: 0.5263 - val_loss: 0.3136 - val_accuracy: 0.6571 Epoch 7/100 - 0s - loss: 1.3985 - accuracy: 0.5211 - val_loss: 0.4132 - val_accuracy: 0.5000 Epoch 8/100 - 0s - loss: 1.0154 - accuracy: 0.5250 - val_loss: 0.1802 - val_accuracy: 0.7929 Epoch 9/100 - 0s - loss: 0.6538 - accuracy: 0.5382 - val_loss: 0.1928 - val_accuracy: 0.7429 Epoch 10/100 - 0s - loss: 0.3917 - accuracy: 0.5461 - val_loss: 0.2226 - val_accuracy: 0.6786 Epoch 11/100 - 0s - loss: 0.3202 - accuracy: 0.5737 - val_loss: 0.2040 - val_accuracy: 0.7000 Epoch 12/100 。。。。。。 Epoch 91/100 - 0s - loss: 0.1849 - accuracy: 0.7605 - val_loss: 0.1677 - val_accuracy: 0.7429 Epoch 92/100 - 0s - loss: 0.1782 - accuracy: 0.7816 - val_loss: 0.2753 - val_accuracy: 0.5857 Epoch 93/100 - 0s - loss: 0.2656 - accuracy: 0.6671 - val_loss: 0.1685 - val_accuracy: 0.7857 Epoch 94/100 - 0s - loss: 0.2607 - accuracy: 0.6684 - val_loss: 0.1785 - val_accuracy: 0.7643 Epoch 95/100 - 0s - loss: 0.1780 - accuracy: 0.7868 - val_loss: 0.1800 - val_accuracy: 0.7429 Epoch 96/100 - 0s - loss: 0.2324 - accuracy: 0.7263 - val_loss: 0.3307 - val_accuracy: 0.5071 Epoch 97/100 - 0s - loss: 0.1957 - accuracy: 0.7250 - val_loss: 0.1646 - val_accuracy: 0.7857 Epoch 98/100 - 0s - loss: 0.1809 - accuracy: 0.7605 - val_loss: 0.1704 - val_accuracy: 0.7643 Epoch 99/100 - 0s - loss: 0.2097 - accuracy: 0.7276 - val_loss: 0.1719 - val_accuracy: 0.7500 Epoch 100/100 - 0s - loss: 0.2314 - accuracy: 0.6842 - val_loss: 0.1709 - val_accuracy: 0.7786 * Accuracy on training set: 89.61% * Accuracy on test set: 77.86%
看起來效果一般。
這裡我將網路加深，修改後的網路如下：
def create_deep_network(input_shape, out_dims=num_classes):
inputs_dim = Input(shape=input_shape)
x = Conv2D(filters=32, kernel_size=3, strides=1, padding='same',
activation='relu')(inputs_dim)
x = Conv2D(filters=32, kernel_size=3, strides=1, padding='same',
activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x = Conv2D(filters=64, kernel_size=3, strides=1, padding='same',
activation='relu')(x)
x = Conv2D(filters=64, kernel_size=3, strides=1, padding='same',
activation='relu')(x)
x = MaxPooling2D(pool_size=(2, 2))(x)
x_flat = Flatten()(x)
fc1 = Dense(512, activation='relu')(x_flat)
dp_1 = Dropout(0.4)(fc1)
fc2 = Dense(out_dims)(dp_1)
fc2 = Activation('softmax')(fc2)
model = Model(inputs=inputs_dim, outputs=fc2)
return model
訓練結果：
- 7s - loss: 0.2834 - accuracy: 0.6355 - val_loss: 0.2863 - val_accuracy: 0.5286 Epoch 2/100 - 2s - loss: 0.1638 - accuracy: 0.7829 - val_loss: 0.1462 - val_accuracy: 0.7714 Epoch 3/100 - 2s - loss: 0.1101 - accuracy: 0.8539 - val_loss: 0.1601 - val_accuracy: 0.7929 Epoch 4/100 - 2s - loss: 0.1067 - accuracy: 0.8592 - val_loss: 0.1240 - val_accuracy: 0.8143 Epoch 5/100 - 2s - loss: 0.0857 - accuracy: 0.8829 - val_loss: 0.1280 - val_accuracy: 0.8429 Epoch 6/100 - 2s - loss: 0.0714 - accuracy: 0.9132 - val_loss: 0.1148 - val_accuracy: 0.8214 Epoch 7/100 - 2s - loss: 0.0549 - accuracy: 0.9382 - val_loss: 0.0855 - val_accuracy: 0.8929 Epoch 8/100 - 2s - loss: 0.0408 - accuracy: 0.9658 - val_loss: 0.0671 - val_accuracy: 0.9214 Epoch 9/100 - 2s - loss: 0.0351 - accuracy: 0.9618 - val_loss: 0.0660 - val_accuracy: 0.9000 Epoch 10/100 - 2s - loss: 0.0253 - accuracy: 0.9750 - val_loss: 0.1011 - val_accuracy: 0.8714 Epoch 11/100 - 2s - loss: 0.0291 - accuracy: 0.9684 - val_loss: 0.0538 - val_accuracy: 0.9214 Epoch 12/100 - 2s - loss: 0.0231 - accuracy: 0.9803 - val_loss: 0.0621 - val_accuracy: 0.9214 Epoch 13/100 - 2s - loss: 0.0192 - accuracy: 0.9882 - val_loss: 0.0498 - val_accuracy: 0.9286 。。。。。。 Epoch 90/100 - 2s - loss: 2.3402e-05 - accuracy: 1.0000 - val_loss: 0.0120 - val_accuracy: 0.9929 Epoch 91/100 - 2s - loss: 1.4936e-05 - accuracy: 1.0000 - val_loss: 0.0127 - val_accuracy: 0.9929 Epoch 92/100 - 2s - loss: 2.3215e-05 - accuracy: 1.0000 - val_loss: 0.0148 - val_accuracy: 0.9857 Epoch 93/100 - 2s - loss: 0.0376 - accuracy: 0.9579 - val_loss: 0.1812 - val_accuracy: 0.8143 Epoch 94/100 - 2s - loss: 0.1855 - accuracy: 0.7987 - val_loss: 0.1621 - val_accuracy: 0.8143 Epoch 95/100 - 2s - loss: 0.1093 - accuracy: 0.8737 - val_loss: 0.1229 - val_accuracy: 0.8500 Epoch 96/100 - 2s - loss: 0.0875 - accuracy: 0.8987 - val_loss: 0.1216 - val_accuracy: 0.8571 Epoch 97/100 - 2s - loss: 0.0973 - accuracy: 0.8882 - val_loss: 0.1086 - val_accuracy: 0.8786 Epoch 98/100 - 2s - loss: 0.0883 - accuracy: 0.8947 - val_loss: 0.1234 - val_accuracy: 0.8429 Epoch 99/100 - 2s - loss: 0.0821 - accuracy: 0.8934 - val_loss: 0.1168 - val_accuracy: 0.8357 Epoch 100/100 - 2s - loss: 0.0376 - accuracy: 0.9513 - val_loss: 0.0460 - val_accuracy: 0.9429 * Accuracy on training set: 97.89% * Accuracy on test set: 94.29%
這時候準確率大大的提高了。。
預測程式碼：
def predict(model_path, image_path1, image_path2, target_size):
saved_model = load_model(model_path, custom_objects={'contrastive_loss': contrastive_loss})
image1 = cv2.imread(image_path1)
image2 = cv2.imread(image_path2)
# 灰度化，並調整尺寸
image1 = cv2.cvtColor(image1, cv2.COLOR_BGR2GRAY)
image1 = cv2.resize(image1, target_size)
image2 = cv2.cvtColor(image2, cv2.COLOR_BGR2GRAY)
image2 = cv2.resize(image2, target_size) # <class 'numpy.ndarray'>
# print(image2.shape) # (80, 80)
# print(image2)
# 對影象資料做scale操作
data1 = np.array([image1], dtype='float') / 255.0 / 255.0
data2 = np.array([image2], dtype='float') / 255.0 / 255.0
print(data1.shape, data2.shape) # (1, 80, 80) (1, 80, 80)
pairs = np.array([data1, data2])
print(pairs.shape) # (2, 80, 80)
y_pred = saved_model.predict([data1, data2])
print(y_pred)
# print(y_pred) # [[4.1023154]]
# pred = y_pred.ravel() < 0.5
# print(pred) # 如果沒有 <0.5則為 [4.1023154] 有的話則是 [False]
# y_true = [1] # 1表示兩個是一個類，0表示不同的類
# if pred == y_true:
# print("是同一類")
# else:
# print("不是同一類")
我們再使用儲存的模型來預測，效果大致上是不錯的，但是還是會有誤識別。可能我的想法還是有點問題。。。。這個我會再學習。
PS：這篇博文主要是自己學習Siamese Network 做的筆記，參考各路大神的筆記，整理於此，然後自己實踐。
參考文獻：https://www.zhihu.com/search?type=content&q=%E5%AD%AA%E7%94%9F%E7%BD%91%E7%BB%9C%E7%9A%84%E5%8E%9F%E7%90%86
https://blog.csdn.net/weixin_45250844/article/details/102765678?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-4&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-4
https://blog.csdn.net/bestrivern/article/details/88605384?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2
https://zhuanlan.zhihu.com/p/29058453
https://github.com/keras-team/keras/blob/master/examples/mnist_siamese.py
關於mnist 資料集訓練Siamese Network的地址：http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
https://sorenbouma.github.io/blog/oneshot/
https://zhuanlan.zhihu.com/p/35040994
https://blog.csdn.net/autocyz/article/details/5314