Java提高篇(二七)-----TreeMap
一、為跟節點
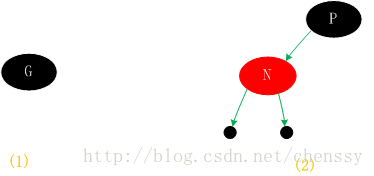
若新插入的節點N沒有父節點,則直接當做根據節點插入即可,同時將顏色設定為黑色。(如圖一(1))
二、父節點為黑色
這種情況新節點N同樣是直接插入,同時顏色為紅色,由於根據規則四它會存在兩個黑色的葉子節點,值為null。同時由於新增節點N為紅色,所以通過它的子節點的路徑依然會儲存著相同的黑色節點數,同樣滿足規則5。(如圖一(2))
(圖一)
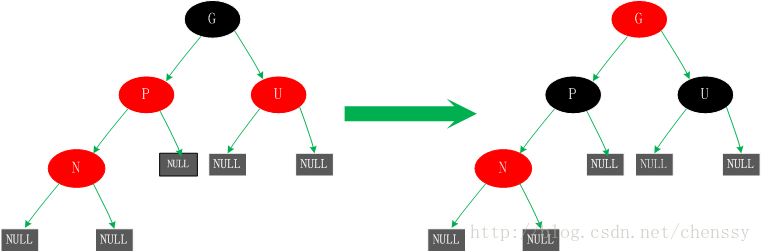
三、若父節點P和P的兄弟節點U都為紅色
對於這種情況若直接插入肯定會出現不平衡現象。怎麼處理?P、U節點變黑、G節點變紅。這時由於經過節點P、U的路徑都必須經過G所以在這些路徑上面的黑節點數目還是相同的。但是經過上面的處理,可能G節點的父節點也是紅色,這個時候我們需要將G節點當做新增節點遞迴處理。
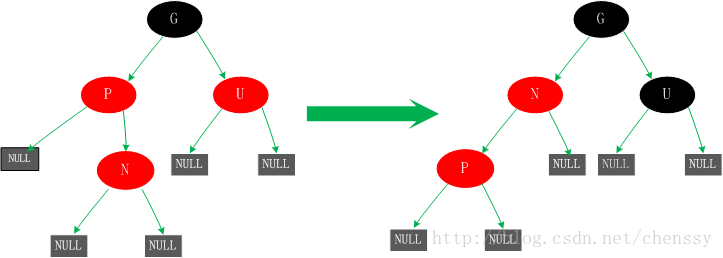
四、若父節點P為紅色,叔父節點U為黑色或者缺少,且新增節點N為P節點的右孩子
對於這種情況我們對新增節點N、P進行一次左旋轉。這裡所產生的結果其實並沒有完成,還不是平衡的(違反了規則四),這是我們需要進行情況5的操作。
五、父節點P為紅色,叔父節點U為黑色或者缺少,新增節點N為父節點P左孩子
這種情況有可能是由於情況四而產生的,也有可能不是。對於這種情況先已P節點為中心進行右旋轉,在旋轉後產生的樹中,節點P是節點N、G的父節點。但是這棵樹並不規範,它違反了規則4,所以我們將P、G節點的顏色進行交換,使之其滿足規範。開始時所有的路徑都需要經過G其他們的黑色節點數一樣,但是現在所有的路徑改為經過P,且P為整棵樹的唯一黑色節點,所以調整後的樹同樣滿足規範5。
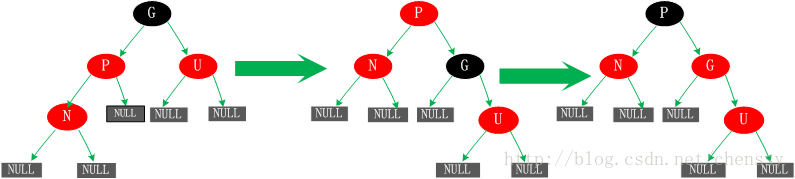
上面展示了紅黑樹新增節點的五種情況,這五種情況涵蓋了所有的新增可能,不管這棵紅黑樹多麼複雜,都可以根據這五種情況來進行生成。下面就來分析Java中的TreeMap是如何來實現紅黑樹的。
TreeMap put()方法實現分析
在TreeMap的put()的實現方法中主要分為兩個步驟,第一:構建排序二叉樹,第二:平衡二叉樹。
對於排序二叉樹的建立,其新增節點的過程如下:
1、以根節點為初始節點進行檢索。
2、與當前節點進行比對,若新增節點值較大,則以當前節點的右子節點作為新的當前節點。否則以當前節點的左子節點作為新的當前節點。
3、迴圈遞迴2步驟知道檢索出合適的葉子節點為止。
4、將新增節點與3步驟中找到的節點進行比對,如果新增節點較大,則新增為右子節點;否則新增為左子節點。
按照這個步驟我們就可以將一個新增節點新增到排序二叉樹中合適的位置。如下:
public V put(K key, V value) {
//用t表示二叉樹的當前節點
Entry<K,V> t = root;
//t為null表示一個空樹,即TreeMap中沒有任何元素,直接插入
if (t == null) {
//比較key值,個人覺得這句程式碼沒有任何意義,空樹還需要比較、排序?
compare(key, key); // type (and possibly null) check
//將新的key-value鍵值對建立為一個Entry節點,並將該節點賦予給root
root = new Entry<>(key, value, null);
//容器的size = 1,表示TreeMap集合中存在一個元素
size = 1;
//修改次數 + 1
modCount++;
return null;
}
int cmp; //cmp表示key排序的返回結果
Entry<K,V> parent; //父節點
// split comparator and comparable paths
Comparator<? super K> cpr = comparator; //指定的排序演算法
//如果cpr不為空,則採用既定的排序演算法進行建立TreeMap集合
if (cpr != null) {
do {
parent = t; //parent指向上次迴圈後的t
//比較新增節點的key和當前節點key的大小
cmp = cpr.compare(key, t.key);
//cmp返回值小於0,表示新增節點的key小於當前節點的key,則以當前節點的左子節點作為新的當前節點
if (cmp < 0)
t = t.left;
//cmp返回值大於0,表示新增節點的key大於當前節點的key,則以當前節點的右子節點作為新的當前節點
else if (cmp > 0)
t = t.right;
//cmp返回值等於0,表示兩個key值相等,則新值覆蓋舊值,並返回新值
else
return t.setValue(value);
} while (t != null);
}
//如果cpr為空,則採用預設的排序演算法進行建立TreeMap集合
else {
if (key == null) //key值為空丟擲異常
throw new NullPointerException();
/* 下面處理過程和上面一樣 */
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//將新增節點當做parent的子節點
Entry<K,V> e = new Entry<>(key, value, parent);
//如果新增節點的key小於parent的key,則當做左子節點
if (cmp < 0)
parent.left = e;
//如果新增節點的key大於parent的key,則當做右子節點
else
parent.right = e;
/*
* 上面已經完成了排序二叉樹的的構建,將新增節點插入該樹中的合適位置
* 下面fixAfterInsertion()方法就是對這棵樹進行調整、平衡,具體過程參考上面的五種情況
*/
fixAfterInsertion(e);
//TreeMap元素數量 + 1
size++;
//TreeMap容器修改次數 + 1
modCount++;
return null;
}上面程式碼中do{}程式碼塊是實現排序二叉樹的核心演算法,通過該演算法我們可以確認新增節點在該樹的正確位置。找到正確位置後將插入即可,這樣做了其實還沒有完成,因為我知道TreeMap的底層實現是紅黑樹,紅黑樹是一棵平衡排序二叉樹,普通的排序二叉樹可能會出現失衡的情況,所以下一步就是要進行調整。fixAfterInsertion(e); 調整的過程務必會涉及到紅黑樹的左旋、右旋、著色三個基本操作。程式碼如下:
/**
* 新增節點後的修復操作
* x 表示新增節點
*/
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED; //新增節點的顏色為紅色
//迴圈 直到 x不是根節點,且x的父節點不為紅色
while (x != null && x != root && x.parent.color == RED) {
//如果X的父節點(P)是其父節點的父節點(G)的左節點
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//獲取X的叔節點(U)
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果X的叔節點(U) 為紅色(情況三)
if (colorOf(y) == RED) {
//將X的父節點(P)設定為黑色
setColor(parentOf(x), BLACK);
//將X的叔節點(U)設定為黑色
setColor(y, BLACK);
//將X的父節點的父節點(G)設定紅色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔節點(U為黑色);這裡會存在兩種情況(情況四、情況五)
else {
//如果X節點為其父節點(P)的右子樹,則進行左旋轉(情況四)
if (x == rightOf(parentOf(x))) {
//將X的父節點作為X
x = parentOf(x);
//右旋轉
rotateLeft(x);
}
//(情況五)
//將X的父節點(P)設定為黑色
setColor(parentOf(x), BLACK);
//將X的父節點的父節點(G)設定紅色
setColor(parentOf(parentOf(x)), RED);
//以X的父節點的父節點(G)為中心右旋轉
rotateRight(parentOf(parentOf(x)));
}
}
//如果X的父節點(P)是其父節點的父節點(G)的右節點
else {
//獲取X的叔節點(U)
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//如果X的叔節點(U) 為紅色(情況三)
if (colorOf(y) == RED) {
//將X的父節點(P)設定為黑色
setColor(parentOf(x), BLACK);
//將X的叔節點(U)設定為黑色
setColor(y, BLACK);
//將X的父節點的父節點(G)設定紅色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//如果X的叔節點(U為黑色);這裡會存在兩種情況(情況四、情況五)
else {
//如果X節點為其父節點(P)的右子樹,則進行左旋轉(情況四)
if (x == leftOf(parentOf(x))) {
//將X的父節點作為X
x = parentOf(x);
//右旋轉
rotateRight(x);
}
//(情況五)
//將X的父節點(P)設定為黑色
setColor(parentOf(x), BLACK);
//將X的父節點的父節點(G)設定紅色
setColor(parentOf(parentOf(x)), RED);
//以X的父節點的父節點(G)為中心右旋轉
rotateLeft(parentOf(parentOf(x)));
}
}
}
//將根節點G強制設定為黑色
root.color = BLACK;
}對這段程式碼的研究我們發現,其處理過程完全符合紅黑樹新增節點的處理過程。所以在看這段程式碼的過程一定要對紅黑樹的新增節點過程有了解。在這個程式碼中還包含幾個重要的操作。左旋(rotateLeft())、右旋(rotateRight())、著色(setColor())。
左旋:rotateLeft()
所謂左旋轉,就是將新增節點(N)當做其父節點(P),將其父節點P當做新增節點(N)的左子節點。即:G.left ---> N ,N.left ---> P。