二叉樹相關題目
二叉樹相關概念
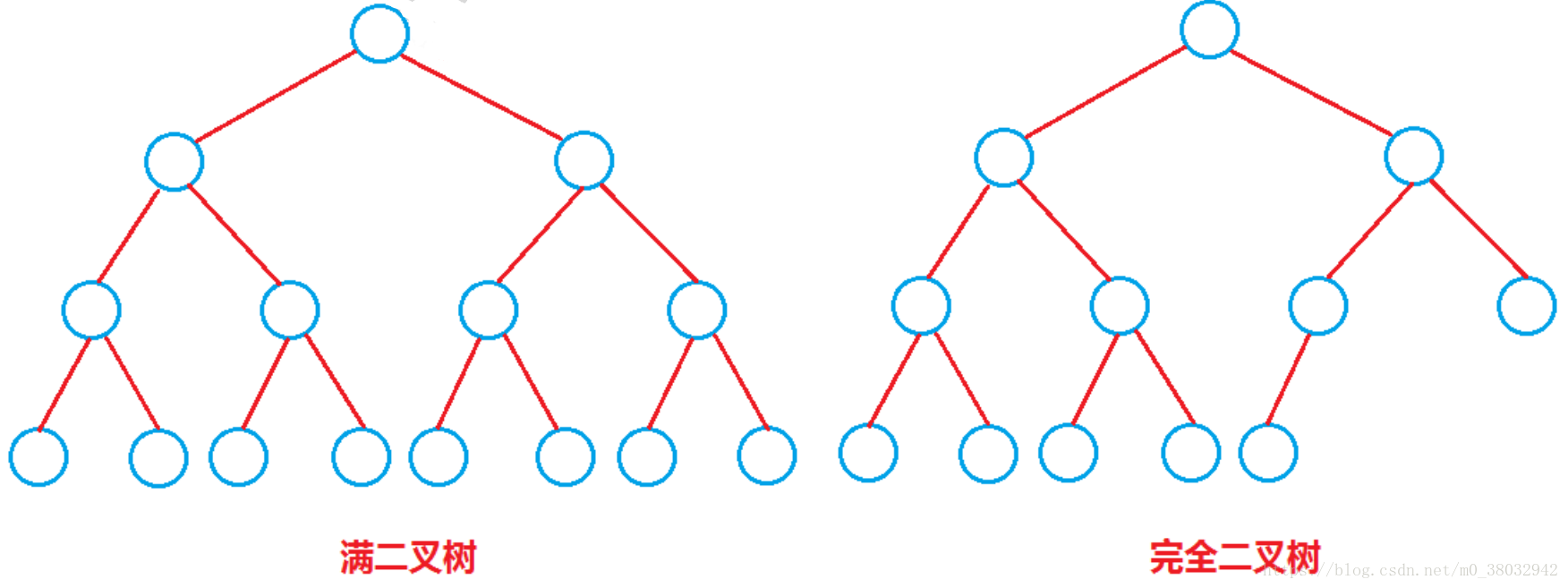
滿二叉樹
在一棵二叉樹中,如果所有分支結點都存在左子樹和右子樹,並且所有葉子節點都在同一層上!
完全二叉樹
如果一棵具有N個結點的二叉樹的結構與滿二叉樹的前N個結點的結構相同,稱為完全二叉樹!
葉子節點
度為0的結點稱為葉結點,葉節點也稱為終端節點,從圖上看就是最下面的一層節點!
二叉樹節點與介面
定義的二叉樹的節點和本次需要實現的介面如下:<BinaryTree.h>
#ifndef __BINARY_TREE_H__
#define __BINARY_TREE_H__
#include <stdio.h>
#include <stdlib.h> 二叉樹的建立
遞迴建立二叉樹
//獲取新節點
static pBTNode BuyBTNode(BTDataType x)
{
pBTNode newNode = (pBTNode)malloc(sizeof(BTNode));
assert(newNode != NULL);
newNode->_left = NULL;
newNode->_right = NULL;
newNode->_data = x;
return newNode;
}
// 建立二叉樹
pBTNode BinaryTreeCreate(BTDataType* a, int n, int *pi)
{
assert(a != NULL);
if ('#' != a[*pi] && (*pi)<n)//這裡還要要求陣列的下標是合法的
{
pBTNode root = BuyBTNode(a[*pi]);
(*pi)++;
root->_left = BinaryTreeCreate(a, n, pi);
(*pi)++;
root->_right = BinaryTreeCreate(a, n, pi);
return root;
}
else
return NULL;
}
char arr[] = { 'A','B','#','C','#',
'#','D','E','#','F',
'#','G','#','#','H','#','#' };
int len = sizeof(arr) / sizeof(arr[0]);
pBTNode root;
int i = 0;
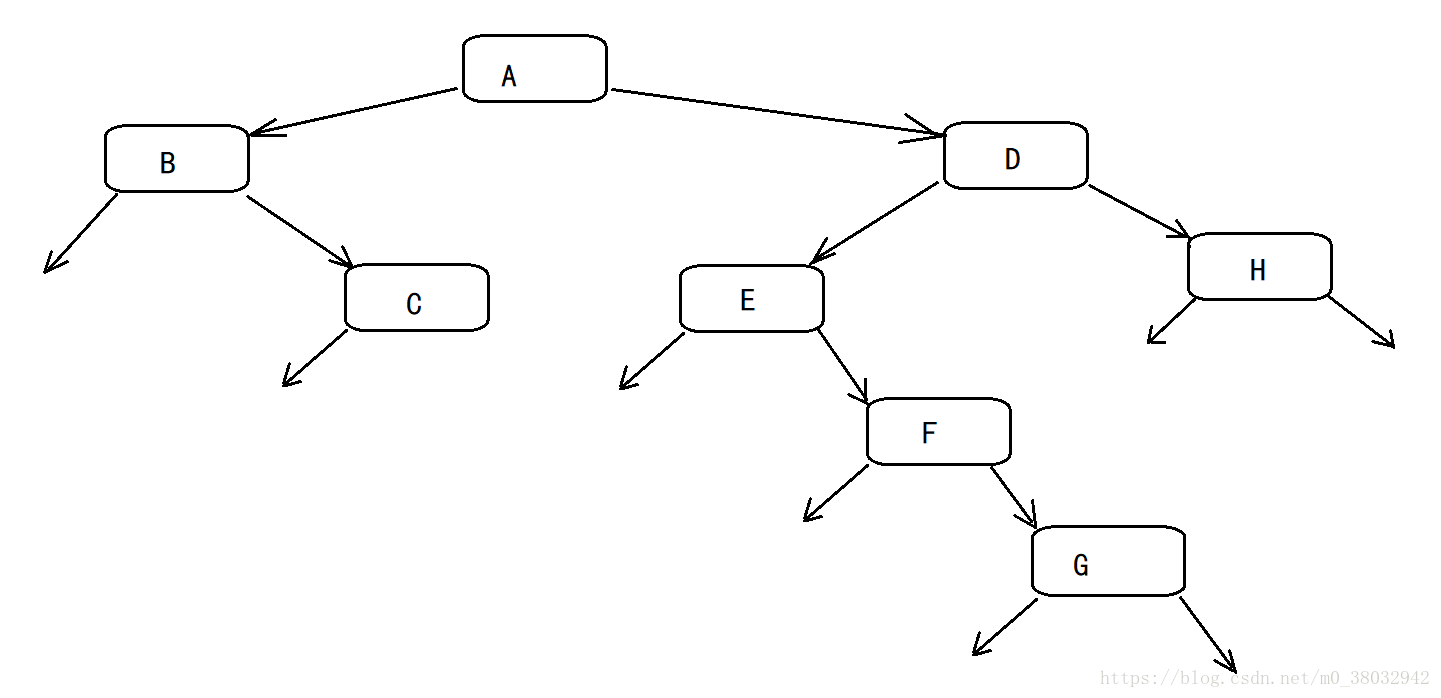
root = BinaryTreeCreate(arr, len, &i);
這樣會創建出這樣一個二叉樹:
二叉樹的遍歷
三種遍歷方式: 前序遍歷、中序遍歷、後序遍歷
前序遍歷PrevOrder的規則
- 根節點
- 遍歷左子樹
- 遍歷右子樹
所以結果應該是:A B C D E F G H
中序遍歷 InOrder的規則
- 遍歷左子樹
- 根節點
- 遍歷右子樹
所以結果應該是:B C A E F G D H
後序遍歷 PostOrder的規則
- 遍歷左子樹
- 遍歷右子樹
- 根節點
所以結果應該是:C B G F E H D A
遞迴遍歷二叉樹
//前序遍歷
void BinaryTreePrevOrder(pBTNode root)
{
if (root == NULL)
return;
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
//中序遍歷
void BinaryTreeInOrder(pBTNode root)
{
if (root->_left != NULL)
BinaryTreeInOrder(root->_left);
printf("%c ", root->_data);
if (root->_right != NULL)
BinaryTreeInOrder(root->_right);
}
//後序遍歷
void BinaryTreePostOrder(pBTNode root)
{
if (root->_left != NULL)
BinaryTreePostOrder(root->_left);
if (root->_right != NULL)
BinaryTreePostOrder(root->_right);
printf("%c ",root->_data);
}
可以看出使用遞迴的方式是非常簡單的,但是遞迴在樹太深的時候也是無法進行遞迴遍歷的,遞迴次數一旦非常多的時候容易發生棧溢位 (Stack Overflow),每次呼叫函式就會建立棧楨,一般情況下棧空間只有幾兆,一旦遞迴次數過多就會溢位!所以應該使用非遞迴的方式對二叉樹進行遍歷!
非遞迴遍歷二叉樹
使用非遞迴遍歷二叉樹需要使用 棧 這種資料結構來輔助完成!
接下來看看非遞迴版本的前序、中序、後序遍歷:
// 前序遍歷-非遞迴遍歷
void BTreePrevOrderNonR(pBTNode root)
{
pBTNode cur = root;
pBTNode top = NULL;
Stack s;
StackInit(&s);
while (cur || StackEmpty(&s) != 0)
{
//訪問左路節點,左路節點進棧
while (cur)
{
printf("%c ", cur->_data);
StackPush(&s, cur);
cur = cur->_left;
}
//棧裡面出來節點,表示左樹已經訪問過
top = StackTop(&s);
StackPop(&s);
//子問題訪問右樹
cur = top->_right;
}
printf("\n");
StackDestory(&s);
}
//中序遍歷-非遞迴遍歷
void BTreeInOrderNonR(pBTNode root)
{
pBTNode cur = root;
pBTNode top = NULL;
Stack s;
StackInit(&s);
while (cur || StackEmpty(&s) != 0)
{
//訪問左路節點,左路節點進棧
while (cur)
{
StackPush(&s, cur);
cur = cur->_left;
}
//棧裡面出來節點,表示左樹已經訪問過
top = StackTop(&s);
printf("%c ", top->_data);
StackPop(&s);
//子問題訪問右樹
cur = top->_right;
}
printf("\n");
StackDestory(&s);
}
後序遍歷比較特殊,需要單獨拿出來說!
在前序遍歷、中序遍歷中根節點都不是最後才會被訪問的元素,然後在後序遍歷中,根節點是最後訪問的元素,所以應該定義一個指標 prev 來防止Top出來的的右指標在不為空的情況下重複進入!
//後序遍歷-非遞迴遍歷
void BTreePostOrderNonR(pBTNode root)
{
pBTNode cur = root;
pBTNode top = NULL;
pBTNode prev = NULL;
Stack s;
StackInit(&s);
while (cur || StackEmpty(&s) != 0)
{
while (cur != NULL)
{
StackPush(&s, cur);
cur = cur->_left;
}
top = StackTop(&s);
if (top->_right == NULL || top->_right == prev)
{
printf("%c ", top->_data);
prev = top;
StackPop(&s);
}
else
{
cur = top->_right;
}
}
}
接著看看另外一種遍歷方式,要保證根結點在左孩子和右孩子訪問之後才能訪問,因此對於任一結點P,先將其入棧。如果P不存在左孩子和右孩子,則可以直接訪問它;或者P存在左孩子或者右孩子,但是其左孩子和右孩子都已被訪問過了,則同樣可以直接訪問該結點。若非上述兩種情況,則將P的右孩子和左孩子依次入棧,這樣就保證了每次取棧頂元素的時候,左孩子在右孩子前面被訪問,左孩子和右孩子都在根結點前面被訪問。
void BTreePostOrderNonR_02(pBTNode root)
{
pBTNode cur = root;
pBTNode top = NULL;
pBTNode prev = NULL;
Stack s;
StackInit(&s);
StackPush(&s,root);
while (StackEmpty(&s) != 0)
{
cur = StackTop(&s);
if ((cur->_left == NULL && cur->_right == NULL) ||
(prev != NULL && (prev == cur->_left || prev == cur->_right)))
{
printf("%c ", cur->_data);
prev = cur;
cur = StackTop(&s);
StackPop(&s);
}
else
{
if (cur->_right != NULL)
StackPush(&s, cur->_right);
if (cur->_left != NULL)
StackPush(&s, cur->_left);
}
}
printf("\n");
StackDestory(&s);
}
這樣非遞迴遍歷二叉樹的方式從表面上看沒有用到遞迴,但是卻用到了遞迴的思想,利用棧這種資料結構,將後遍歷的節點先壓棧,最後出棧便可以的到我們想要的結果,又避開了直接使用遞迴的明顯缺點,這樣利用棧作為輔助資料結構的方法便是將遞迴問題轉化為非遞迴問題的根本所在!
層序遍歷二叉樹、滿二叉樹的判斷
層序遍歷就是一層一層的遍歷,這裡需要用到佇列這種資料結構!
層序遍歷的原理也是非常簡單,先將根節點入棧,在根節點出棧的時候將根節點的左節點和右節點入棧,然後在左節點和右節點出棧的時候就分別將它們的左節點和右節點入棧,這樣就把每一層的節點入佇列,出佇列的時候自然就是層序遍歷了,程式碼如下:
//層序遍歷,需要使用佇列
void BTreeLevelOrder(pBTNode root)
{
Queue qu;
QueueInit(&qu);
if (root != NULL)
QueuePush(&qu, root);
while (QueueEmpty(&qu) != 0)
{
DataType ret = QueueFront(&qu);
printf("%c ", ret->_data);
QueuePop(&qu);
if (ret->_left != NULL)
QueuePush(&qu, ret->_left);
if (ret->_right != NULL)
QueuePush(&qu, ret->_right);
}
printf("\n");
QueueDestory(&qu);
}
判斷是否是滿二叉樹其實就是考察層序遍歷的應用,在遍歷的過程中只要遇到一個是NULL,那麼後面都應該為空才能算是完全二叉樹,否則直接返回0,程式碼如下:
// 判斷完全二叉樹 ,是就返回1,不是返回0
int IsCompleteBTree(pBTNode root)
{
Queue qu;
QueueInit(&qu);
if (root != NULL)
QueuePush(&qu, root);
while (QueueEmpty(&qu) != 0)
{
DataType ret = QueueFront(&qu);
QueuePop(&qu);
if (ret != NULL)
{
QueuePush(&qu, ret->_left);
QueuePush(&qu, ret->_right);
}
else
break;
}
while (QueueEmpty(&qu) != 0)
{
DataType ret = QueueFront(&qu);
if (ret != NULL)
return 0;
else
QueuePop(&qu);
}
//QueueDestory(&qu);
return 1;
}
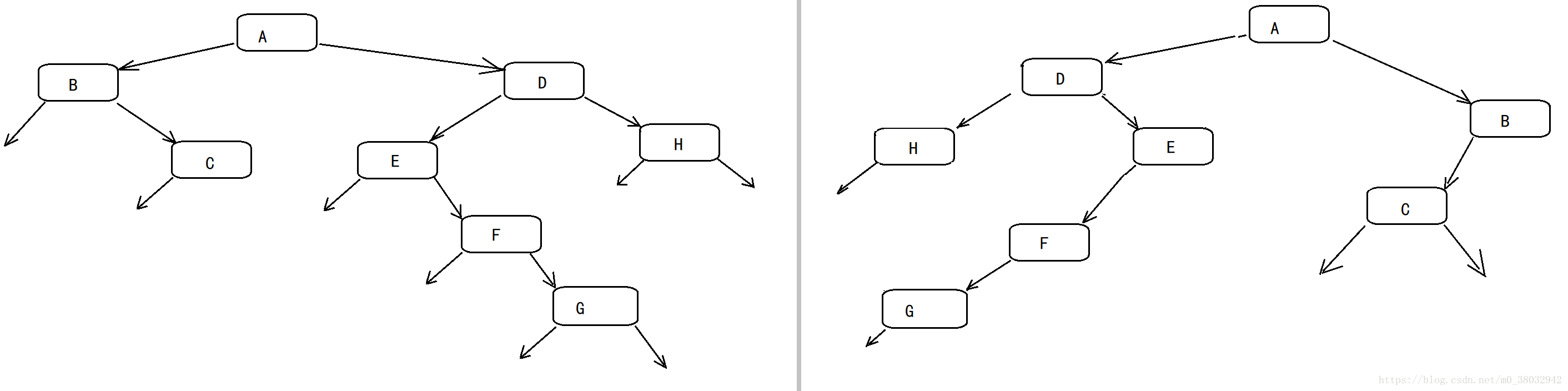
求二叉樹的映象
如圖所示,這就是互為映象的兩個二叉樹,接下來使用遞迴和非遞迴方式求出二叉樹的映象:
//求映象的遞迴方式
void GetMirror_R(pBTNode root)
{
pBTNode tmp = NULL;
if (root == NULL)
return;
GetMirror(root->_left);
GetMirror(root->_right);
tmp = root->_left;
root->_left = root->_right;
root->_right = tmp;
}
//非遞迴方式
void GetMirror(pBTNode root)
{
pBTNode tmp = NULL;
Queue qu;
QueueInit(&qu);
if (root != NULL)
QueuePush(&qu, root);
while (QueueEmpty(&qu) != 0)
{
DataType ret = QueueFront(&qu);
QueuePop(&qu);
if (ret->_left != NULL)
QueuePush(&qu, ret->_left);
if (ret->_right != NULL)
QueuePush(&qu, ret->_right);
tmp = ret->_left;
ret->_left = ret->_right;
ret->_right = tmp;
}
}
二叉樹的其他問題
//返回節點個數
size_t BTreeSize(pBTNode root)
{
if (root == NULL)
return 0;
return BTreeSize(root->_left) + BTreeSize(root->_right) +1;
}
//返回葉子節點的個數
size_t BTreeLeafSize(pBTNode root)
{
if (root == NULL)
return 0;
if (root->_left == NULL && root->_right == NULL)
return 1;
return BTreeLeafSize(root->_left) + BTreeLeafSize(root->_right);
}
//返回第K層節點個數
size_t BTreeKLevelSize(pBTNode root, size_t k)
{
if (root == NULL)
return 0;
if (k == 1)
return k;
return BTreeKLevelSize(root->_left, k - 1) + BTreeKLevelSize(root->_right, k - 1);
}
//返回樹的深度
size_t BTreeDepth(pBTNode root)
{
int leftDeph = 0;
int rightDeph = 0;
if (root == NULL)
return 0;
leftDeph = BTreeDepth(root->_left)+1;
rightDeph = BTreeDepth(root->_right)+1;
return leftDeph > rightDeph ? leftDeph : rightDeph;
}
//返回值為x的節點地址
pBTNode BTreeFind(pBTNode root, BTDataType x)
{
pBTNode ret = NULL;
if (root == NULL||root->_data == x)
return root;
ret = BTreeFind(root->_left, x);
if (ret != NULL)
return ret;
return BTreeFind(root->_right, x);
}
//銷燬函式
void BinaryTreeDestory(pBTNode* proot)
{
if (proot == NULL || *proot == NULL)
return;
if ((*proot)->_left != NULL)
BinaryTreeDestory(&((*proot)->_left));
if ((*proot)->_right != NULL)
BinaryTreeDestory(&((*proot)->_right));
free(*proot)
相關推薦
二叉樹相關題目
二叉樹相關概念
滿二叉樹
在一棵二叉樹中,如果所有分支結點都存在左子樹和右子樹,並且所有葉子節點都在同一層上!
完全二叉樹
如果一棵具有N個結點的二叉樹的結構與滿二叉樹的前N個結點的結構相同,稱為完全二叉樹!
葉子節點
度為0的結點稱為葉結點,葉節點也稱為終端
LeetCode:二叉樹相關應用
div mage alt sed note col from ret 題目 LeetCode:二叉樹相關應用
基礎知識
617.歸並兩個二叉樹
題目
Given two binary trees and imagine that when you put one of th
二叉樹相關
賦值 進行 n) 後序 復雜 很好 時間 葉子 style BST:
增:(插入)
? 若當前的二叉查找樹為空,則插入的元素為根節點,
? 若插入的元素值小於根節點值,則將元素插入到左子樹中,
? 若插入的元素值不小於根節點值,則將元素插入到右子樹中
簡單二叉樹相關代碼
\n include reat oid 結構 存儲空間 root node branch
1 #include <stdio.h>
2
3 typedef struct tagBinaryTree* Node;
4 typedef s
二叉樹常見題目
dep height tree right pre 個數 二叉樹 節點 leaf 一、求二叉樹的最大深度
public int maxDepth(Node node){
if(node == null) return 0;
int left
鏈表,二叉樹相關算法的簡單整理
kmp 誰的 指針 感覺 它的 左右子樹 排序 原理 鏡像 最近在刷牛客網的劍指offer的題,感覺自己的編程能力還是很差,有時候有思路但是總是需要調試蠻久的時間,但是練習的太少。
鏈表
A->B->C->D
簡單的說單鏈表就是一個當前的節點只指向鏈表
二叉樹相關知識總結(二)
是否 integer string 根節點 color ast creat postorder ray 二叉樹的Java實現
一、分析
一個二叉樹節點包含三個部分,分別是,指向左子樹的部分,指向右子樹的部分,數據部分,如下圖所示:
我們是否可以將每個節點都抽象為一個
用Python實現二叉樹相關
程式碼如下:
class Node(object):
""""""
def __init__(self, item):
self.elem = item
self.lchild = None
self.rchild = No
二叉樹相關概念
一. 二叉樹基本概念
在電腦科學中,二叉樹是每個結點最多有兩個子樹的樹結構。通常子樹被稱作“左子樹”(left subtree)和“右子樹”(right subtree)。二叉樹常被用於實現二叉查詢樹和二叉堆。二叉樹是每個結點最多有兩個子樹的樹結構。它有五種基本形態:二叉樹可以是空集;根可以有空的左子樹或右
與二叉樹相關的演算法筆試題集
1. 二叉搜尋樹(BST)的後序遍歷序列
2. 序列化/反序列化二叉樹
3. 找到BST中的第k小的數
4. 二叉搜尋樹轉雙鏈表
5. 找出所有節點和滿足目標數的路徑
6.根據二叉樹的前序遍歷和中序遍歷陣列來重建二叉樹
7
資料結構—二叉樹相關概念及經典面試題
二叉樹概念
一棵二叉樹是結點的有限集合,該集合或者為空, 或者是由根結點加上兩棵分別稱為左子樹和右子樹的二叉樹構成
二叉樹的特點:
每個結點最多有兩棵子樹,即二叉樹不存在度大於2的結點
二叉樹的子樹有左右之分,其子樹的次序不能顛倒
滿二叉樹、完全二叉樹
【面試題】二叉樹相關
1.二叉樹
二叉樹是每個節點最多有兩個子樹的樹結構
滿二叉樹:除葉子節點外,所有節點的度都為2
完全二叉樹:葉子結點只能出現在最下兩層;最下層的葉子一定集中在左部連續位置;倒數二層,若有葉子結點,一定都在右部連續位置;如果結點度為1 ,則該結點只有左孩子,即
二叉樹相關基礎知識總結
block spa play 概念 中序 森林 sel 就是 ima 一:樹的概念
樹是一種數據結構,它是由n(n>=1)個有限結點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。它具有
和二叉樹相關的面試題
所謂的二叉樹就是樹中的每個節點最多有兩個孩子節點。滿二叉樹:除最後一層沒有子節點外,其它層的節點都具有兩個子節點。完全二叉樹:若二叉樹的高度為h,除最後一層外,其它層的節點數目都達到最大,並且最後一層
二叉樹相關筆試面試題(一)
本部落格內容
一、二叉樹的結構
二、求二叉樹中節點個數
三、求二叉樹的第k層的節點個數
四、求二叉樹的葉子節點的個數
五、求二叉樹的深度
六、二叉樹的遍歷(前序、中序、後序)
七、層序遍歷二叉樹(從上到下、從左到右)
八、將二叉搜尋樹變為有序的雙
java面試程式設計題(二叉樹相關)
題目:
輸入某二叉樹的前序遍歷和中序遍歷的結果,請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重複的數字。例如輸入前序遍歷序列{1,2,4,7,3,5,6,8}和中序遍歷序列{4,7,2,1,5,3,8,6},則重建二叉樹並返回。
二叉樹結構為
java資料結構與之二叉樹相關實現(第一篇:遍歷)
一、基本概念
每個結點最多有兩棵子樹,左子樹和右子樹,次序不可以顛倒。 性質:
非空二叉樹的第n層上至多有2^(n-1)個元素。
深度為h的二叉樹至多有2^h-1個結點。
滿二叉樹:所有終端都在同一層次,且非終端結點的度數為2。 在滿二叉
【面試題】二叉樹相關面試題
判斷二叉樹是否是平衡二叉樹
可以分兩步實現。第一步先遍歷二叉樹中的每一個結點node,呼叫height()求出該結點的左子樹高度height(node.left) 和 右子樹高度 height(node.right)。根據左右子樹的高度差是否滿足其絕對值不超
整理五道演算法題系列(1)二叉樹相關
背景
最近想整理一些有意思的題目,特別是給力的破題技巧與思想,均為學習筆記,於此做個長期記錄。不多說,進入演算法世界了~~
說明
=> 五道 / 篇
=> Java
=> 二叉樹相關
題目
1、重建二叉樹
輸入某二叉
面試題(二叉樹相關)
// 二叉樹有關的操作
#include "stdafx.h"
#include "CommonDataStruct.h"
#include <stddef.h>
#include <stack>
#include <queue>
/