Description

Flappy Bird是一款風靡一時的休閒手機遊戲。玩家需要不斷控制點選手機螢幕的頻率來調節小鳥的飛行高度，讓小鳥順利通過畫面右方的管道縫隙。如果小鳥一不小心撞到了水管或者掉在地上的話，便宣告失敗。

現在小鳥們(n只)遇到了一個難題，他們遇到了一堵巨大的牆，牆上僅有m個洞供他們通過，由於小鳥們的體型不同且牆上洞的形狀也不同，所以每種體型的鳥通過每個洞的時間都不同，鳥的體型共有n種，第i種體型的鳥通過第j個洞需要的時間記為T(i,j)，且一個洞必須前一隻鳥通過之後後一隻鳥才能開始通過。

從時刻0開始，鳥開始通過，而每一隻鳥的等待時間為從時刻0到自己已經通過洞的時間。現在知道了第i種體型的鳥有pi只，請求出使所有鳥都通過牆的最少的等待時間之和。

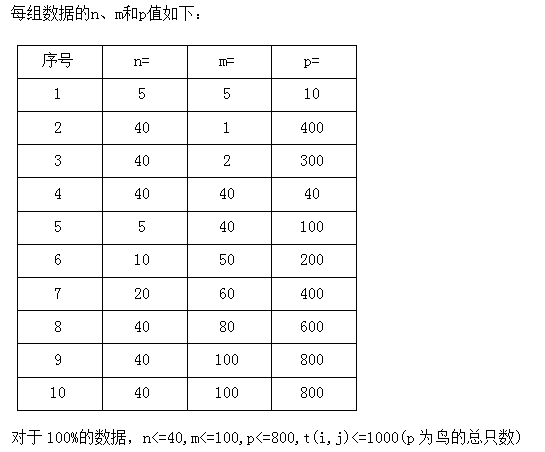
Data Constraint

Solution

看到這種題首先就想到了網路流（問：恩！？等等！！，網路流是NOIP提高組的？別嚇我！ 答：別問我，我也不知道，反正題目就擺在那，我在比賽時也別嚇到了，搞到我第一時間就否決了網路流的想法，拼死去想了一個小時dp，毛都沒有！！！）

我們考慮用費用流解決這道題。首先源點向第i種小鳥連一條流量為pi，費用為0的邊，接著將每個洞拆成p個洞（p為小鳥總數）。每隻小鳥分別向m* p個洞連一條流量為1，費用為 f(m,n)* 1，f(m,n)* 2，f(m,n)* 3，…… ，f(m,n)* p。m* p個洞分別向匯點連一條流量為1，費用為0的邊。

由於有m*p=80000個洞，40種小鳥，總共會連3.2 10

6，條邊，邊數太過巨大！！！，所以我們考慮動態加邊。具體操作為：我們會發現，對於第i個洞，不流第一個費用為f(i,j),反而流第二個費用為f(i,j) 2顯然不優，所以我們對於第一個洞，只有流滿第一個費用為f(i,j),才建流第二個費用為f(i,j)* 2邊，即每種小鳥向新建的點連一條流量為1，費用為f(i,j)*2的邊。

程式碼

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=6600000,maxn1=802;
int first[maxn
 
],last[maxn],next[maxn],value[maxn],cost[maxn],d[maxn],dui[maxn],bz[maxn],a[maxn1][maxn1];
int n,m,num,x,i,t,j,k,l,ans,p,m1;
void lian(int x,int y,int z,int z1){
    last[++num]=y;value[num]=z;cost[num]=z1,next[num]=first[x];first[x]=num;
}
int pan(int x){
    if (x%m) return x%m;return m;
}
int pan1(int x){
    if (x%m) return x/m;return x/m-1;
}
int dg(int x,int sum){
    if (x==n+m*maxn1+1){
        ans+=d[0]*sum;
        return sum;
    }
    int t,k,q=sum,l;
    bz[x]=p;
    for (t=first[x];t;t=next[t])
        if (bz[last[t]]!=p && d[x]==d[last[t]]+cost[t] && value[t]){
            k=dg(last[t],min(q,value[t]));
            if (k){
                value[t]-=k;
                value[dui[t]]+=k;
                if (last[t]==n+m*maxn1+1){
                    for (i=1;i<=n;i++){
                        l=a[i][pan(x-n)]*(pan1(x-n)+2);
                        lian(i,x+m,1,l),lian(x+m,i,0,-l),dui[num]=num-1,dui[num-1]=num;
                    }
                    lian(x+m,n+m*maxn1+1,1,0),lian(n+m*maxn1+1,x+m,0,0),dui[num]=num-1,dui[num-1]=num;
                }
                q-=k;
                if (!q) break;
            }
        }
    return sum-q;
}
bool pan(){
    if (!p) return true;
    int i,j,t,k=maxn,l;
    for (i=0;i<=n+m*maxn1+1;i++)
        if (bz[i]==p)
            for (t=first[i];t;t=next[t])
                if (bz[last[t]]!=p && value[t]) k=min(k,d[last[t]]+cost[t]-d[i]);
    if (k==maxn) return false;
    for (i=0;i<=n+m*maxn1+1;i++)
        if (bz[i]==p) d[i]+=k;
    return true;
}
int main(){
//  freopen("data.in","r",stdin);
    scanf("%d%d",&n,&m);
    for (i=1;i<=n;i++)
        scanf("%d",&x),lian(0,i,x,0),lian(i,0,0,0),dui[num]=num-1,dui[num-1]=num;
    for (i=1;i<=n;i++)
        for (j=1;j<=m;j++){
            scanf("%d",&x);a[i][j]=x;
            lian(i,n+j,1,x),lian(n+j,i,0,-x),dui[num]=num-1,dui[num-1]=num;
        }
    for (i=n+1;i<=n+m;i++)
        lian(i,n+m*maxn1+1,1,0),lian(n+m*maxn1+1,i,0,0),dui[num]=num-1,dui[num-1]=num;
    while (pan()){
        p++;
        while (dg(0,maxn)) p++;
    }
    printf("%d\n",ans);
}