Description

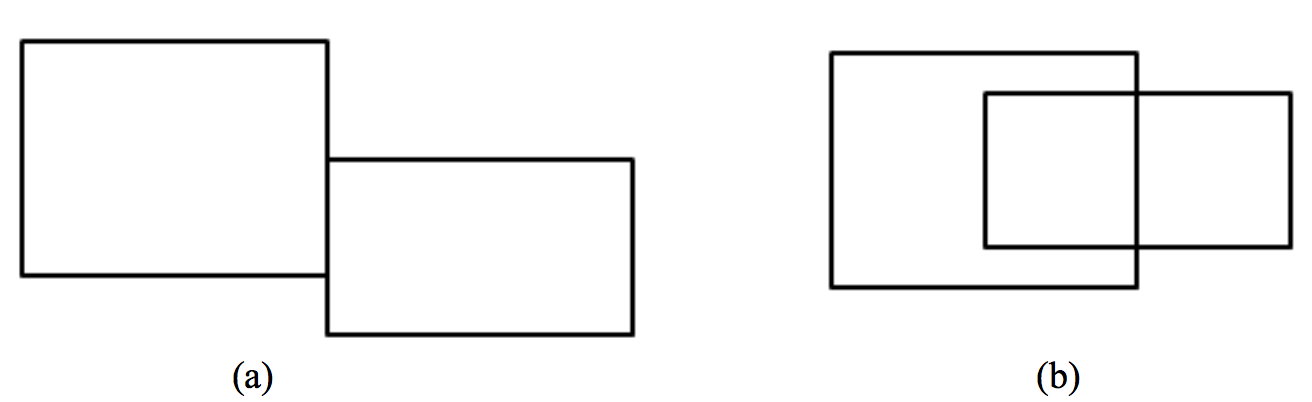
給定兩個簡單多邊形,你的任務是判斷二者是否有面積非空的公共部分。如下圖,(a)中的兩個

矩形只有一條公共線段,沒有公共面積。

在本題中,簡單多邊形是指不自交(也不會接觸自身)、不含重複頂點並且相鄰邊不共線的多
邊形。

注意:本題並不複雜,但有很多看上去正確的演算法實際上暗藏缺陷,請仔細考慮各種情況。

Input
輸入包含不超過 100 組資料。每組資料包含兩行,每個多邊形佔一行。多邊形的格式是:第一 個整數 n 表示頂點的個數 (3<=n<=100),接下來是 n 對整數(x,y) (-1000<=x,y<=1000),即多邊 形的各個頂點,按照逆時針順序排列。

Output
對於每組資料,如果有非空的公共部分,輸出”Yes”,否則輸出”No”。

Sample Input

4 0 0 2 0 2 2 0 2
4 2 0 4 0 4 2 2 2
4 0 0 2 0 2 2 0 2
4 1 0 3 0 3 2 1 2

Sample Output

Case 1: No
Case 2: Yes

Hint

無

直接求連個多邊形的面積交。。這裡有可能是凹邊形。所以用三角劃分的辦法求。（直接半平面交的話。。一直wa）.最最坑的一點。求出的面積>0wa了。而面積>eps過了。。。（臥槽啊）。

#include<cstdio>
#include<cmath>
 

#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<queue>
#include<map>
#include<stack>
#include<set>

using namespace std;

const int maxn=555;
const int maxisn=10;
const double eps=1e-8;
const double pi=acos(-1.0);

int
 
 dcmp(double x){
    if(x>eps) return 1;
    return x<-eps ? -1 : 0;
}
inline double Sqr(double x){
    return x*x;
}
struct Point{
    double x,y;
    Point(){x=y=0;}
    Point(double x,double y):x(x),y(y){};
    friend Point operator + (const Point &a,const Point &b) {
        return Point(a.x+b.x,a.y+b.y);
    }
    friend Point operator - (const Point &a,const Point &b) {
        return Point(a.x-b.x,a.y-b.y);
    }
    friend bool operator == (const Point &a,const Point &b) {
        return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
    }
    friend Point operator * (const Point &a,const double &b) {
        return Point(a.x*b,a.y*b);
    }
    friend Point operator * (const double &a,const Point &b) {
        return Point(a*b.x,a*b.y);
    }
    friend Point operator / (const Point &a,const double &b) {
        return Point(a.x/b,a.y/b);
    }
    friend bool operator < (const Point &a, const Point &b) {
        return a.x < b.x || (a.x == b.x && a.y < b.y);
    }
    inline double dot(const Point &b)const{
        return x*b.x+y*b.y;
    }
    inline double cross(const Point &b,const Point &c)const{
        return (b.x-x)*(c.y-y)-(c.x-x)*(b.y-y);
    }

};

Point LineCross(const Point &a,const Point &b,const Point &c,const Point &d){
    double u=a.cross(b,c),v=b.cross(a,d);
    return Point((c.x*v+d.x*u)/(u+v),(c.y*v+d.y*u)/(u+v));
}
double PolygonArea(Point p[],int n){
     if(n<3) return 0.0;
     double s=p[0].y*(p[n-1].x-p[1].x);
     p[n]=p[0];
     for(int i=1;i<n;i++){
        s+=p[i].y*(p[i-1].x-p[i+1].x);
     }
     return fabs(s*0.5);
}
double CPIA(Point a[],Point b[],int na,int nb){
    Point p[maxisn],temp[maxisn];
    int i,j,tn,sflag,eflag;
    a[na]=a[0],b[nb]=b[0];
    memcpy(p,b,sizeof(Point)*(nb+1));
    for(i=0;i<na&&nb>2;++i){
        sflag=dcmp(a[i].cross(a[i+1],p[0]));
        for(j=tn=0;j<nb;++j,sflag=eflag){
            if(sflag>=0) temp[tn++]=p[j];
            eflag=dcmp(a[i].cross(a[i+1],p[j+1]));
            if((sflag^eflag)==-2)
                temp[tn++]=LineCross(a[i],a[i+1],p[j],p[j+1]);
        }
        memcpy(p,temp,sizeof(Point)*tn);
        nb=tn,p[nb]=p[0];
    }
    if(nb<3) return 0.0;
    return PolygonArea(p,nb);
}
double SPIA(Point a[],Point b[],int na,int nb){
    int i,j;
    Point t1[4],t2[4];
    double res=0.0,if_clock_t1,if_clock_t2;
    a[na]=t1[0]=a[0];
    b[nb]=t2[0]=b[0];
    for(i=2;i<na;i++){
        t1[1]=a[i-1],t1[2]=a[i];
        if_clock_t1=dcmp(t1[0].cross(t1[1],t1[2]));
        if(if_clock_t1<0) swap(t1[1],t1[2]);
        for(j=2;j<nb;j++){
            t2[1]=b[j-1],t2[2]=b[j];
            if_clock_t2=dcmp(t2[0].cross(t2[1],t2[2]));
            if(if_clock_t2<0) swap(t2[1],t2[2]);
            res+=CPIA(t1,t2,3,3)*if_clock_t1*if_clock_t2;
        }
    }
    return res;
    //return PolygonArea(a,na)+PolygonArea(b,nb)-res;
}

Point a[222],b[222];
Point aa[222],bb[222];

int main(){
    int n1,n2;
    int cas=0;
    while(scanf("%d",&n1)!=EOF){
        for(int i=0;i<n1;i++) scanf("%lf %lf",&a[i].x,&a[i].y);
        scanf("%d",&n2);
        for(int i=0;i<n2;i++) scanf("%lf %lf",&b[i].x,&b[i].y);

        if(fabs(SPIA(a,b,n1,n2))>eps) printf("Case %d: Yes\n",++cas);
        else printf("Case %d: No\n",++cas);
    }
    return 0;
}