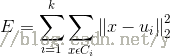定義     俗話說“物以類聚”，其實從廣義上說，聚類就是將資料集中在某些方面相似的資料成員放在一起。一個聚類就是一些資料例項的集合，其中處於相同聚類中的資料元素彼此相似，但是處於不同聚類中的元素彼此不同。

由於在聚類中那些表示資料類別的分類或分組資訊是沒有的，即這些資料是沒有標籤的，所有聚類及時通常被成為無監督學習（UnsupervisedLearning）。

基本思想

    給定一個有N個物件的資料集，構造資料的K個簇，K<=N。滿足下列條件：

1.每個簇至少包含一個物件

2.每一個物件屬於且僅屬於一個簇

3.將滿足於上述條件的K個簇稱作一個合理劃分

對於給定的類別數目K，首先給出初始化分，通過迭代改變樣本和簇的隸屬關係，使得每一次改進之後的劃分方案都較前一次好。

ØK-Means演算法，也被稱為K-平均或K-均值，是一種廣泛使用的聚類演算法，或者成為其他聚類演算法的基礎。 ØStep1：隨機選取K個樣本點作為簇中心

從資料集中隨機選擇

k個數據點作為初始大哥（質心，Centroid）

ØStep2：將其他樣本點根據其與簇中心的距離，劃分給最近的簇

對集合中每一個小弟，計算與每一個初始大哥的距離，離哪個初始大哥距離近，就跟定哪個大哥。

ØStep3：更新各簇的均值向量，將其作為新的簇中心

這時每一個大哥手下都聚集了一群小弟，重新進行選舉，每一群選出新的大哥（通過演算法選出新的質心）。

ØStep4：若所有簇中心未發生改變，則停止；否則執行Step2

如果新大哥和老大哥之間的距離小於某一個設定的閾值或未發生變化（表示重新計算的質心的位置變化不大，趨於穩定，或者說收斂），可以認為我們進行的聚類已經達到期望的結果，演算法終止。否則重新迭代。

Ø演算法描述

演算法的時間複雜度是O(K*N*T)，

k是中心點個數，

N資料集的大小，

T是迭代次數。

"k均值"（k-means）演算法就是針對聚類劃分最小化平方誤差：

其中是簇Ci的均值向量。從上述公式中可以看出，該公式刻畫了簇內樣本圍繞簇均值向量的緊密程度，E值越小簇內樣本的相似度越高。

舉例

Ø描述：

 列舉6個點，分成兩堆，前三個點一堆，後三個點是另一堆，手動執行K-means

                         

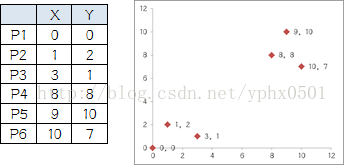
Ø執行過程： Ø1.選擇初始大哥：隨機選擇P1，P2 Ø2.計算小弟和大哥的距離：P3到P1的距離從圖上也能看出來（勾股定理），是√10 = 3.16；P3到P2的距離√((3-1)^2+(1-2)^2 = √5 = 2.24，所以P3離P2更近，P3就跟P2。同理，P4、P5、P6也這麼算。組

A：P1組B：P2、P3、P4、P5、P6 Ø3.重新選舉：組A沒啥可選的，大哥還是P1自己
組B有五個人，需要選新大哥，這裡要注意選大哥的方法是每個人X座標的平均值和Y座標的平均值組成的新的點，為新大哥，也就是說這個大哥是“虛擬的”。
因此，B組選出新大哥的座標為：P哥（（1+3+8+9+10）/5，（2+1+8+10+7）/5）=（6.2，5.6）。綜合兩組，新大哥為P1（0，0），P哥（6.2，5.6），而P2-P6重新成為小弟 Ø4.再次計算小弟到大哥的距離：這時可以看到P2、P3離P1更近，P4、P5、P6離P哥更近，所以第二次站隊的結果是：   組A：P1、P2、P3，組B：P4、P5、P6（虛擬大哥這時候消失） Ø5.第二次選舉：按照上一次選舉的方法選出兩個新的虛擬大哥：P哥1（1.33，1）P哥2（9，8.33），P1-P6都成為小弟 Ø6.第三次計算小弟到大哥的距離：這時可以看到P1、P2、P3離P哥1更近，P4、P5、P6離P哥2更近，所以第二次站隊的結果是：組A：P1、P2、P3組B：P4、P5、P6。這次站隊的結果和上次沒有任何變化了，說明已經收斂，聚類結束，聚類結果和我們最開始設想的結果完全一致。 k值的選取

通常的做法是多嘗試幾個K值，看分成幾類的結果更好解釋，更符合分析目的。

或者按遞增的順序嘗試不同的k值，同時畫出其對應的誤差值，通過尋求拐點來找到一個較好的k值。

中心點的選取（質心）

1、選擇彼此距離儘可能遠的那些點作為中心點；（具體來說就是先選第一個點，然後選離第一個點最遠的當第二個點，然後選第三個點，第三個點到第一、第二兩點的距離之和最小，以此類推）

2、先採用層次進行初步聚類輸出k個簇，以簇的中心點的作為k-means的中心點的輸入。

3、多次隨機選擇中心點訓練k-means，選擇效果最好的聚類結果。

質心的距離

 

實驗方案

方案描述：採用keel-dataset的資料集中籃球運動員資料，每分鐘助攻數、身高、每分鐘得分數。通過該資料集判斷一個籃球運動員屬於什麼位置（後衛、前鋒、中鋒）或（控衛，分衛，小前鋒，大前鋒，中鋒）

資料集地址：KEEL-dataset- Basketball dataset

資料集特徵：assists_per_minute（每分鐘助攻數） height（運動員身高）time_played（運動員出場時間）age（運動員年齡）points_per_minute（每分鐘得分數）

實驗結果
ØK值取3（後衛、前鋒、中鋒） Ø初始化k個質心，利用radom函式隨機獲取

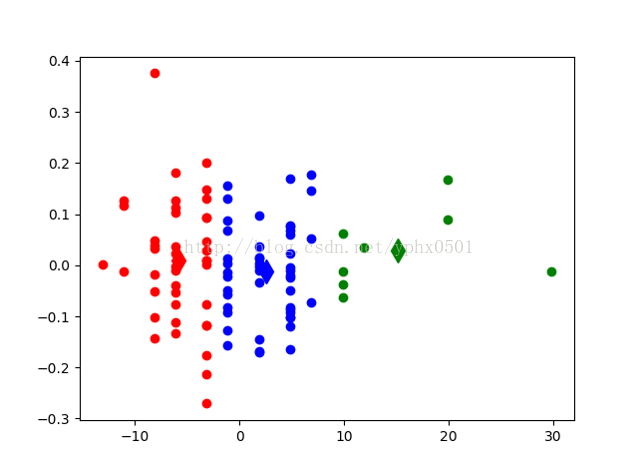
ØK值取5（控衛、分衛、小前鋒、大前鋒、中鋒） 初始化k個質心，利用radom函式隨機獲取


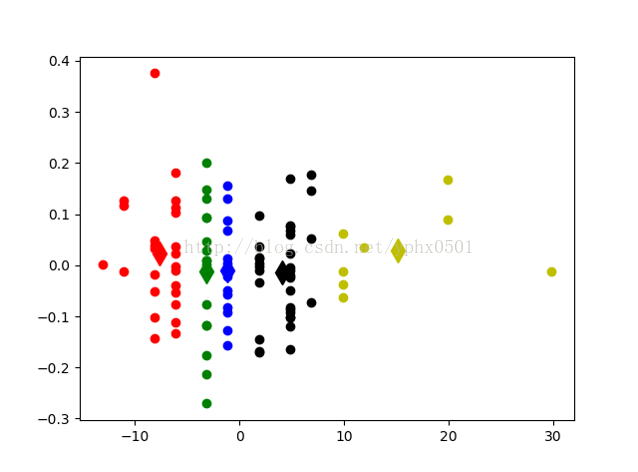
程式碼

# -*- coding: UTF-8 -*-
import numpy
import random
import codecs
import copy
import re
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
import numpy as np
def calcuDistance(vec1, vec2):
    # 計算向量vec1和向量vec2之間的歐氏距離
return numpy.sqrt(numpy.sum(numpy.square(vec1 - vec2)))


def loadDataSet(inFile):
    # 載入資料測試資料集
    # 資料由文字儲存，為五維座標
inDate = codecs.open(inFile, 'r', 'utf-8').readlines()
    dataSet1 = list()
    dataSet = list()
    for line in inDate:
        line = line.strip()
        strList = re.split('[ ]+', line)  # 去除多餘的空格
        #print (strList[0], strList[1],strList[2], strList[3], strList[4])
numList = list()
        for item in strList:
            num = float(item)
            numList.append(num)
            #print (numList)
dataSet.append(numList)
        #X = dataSet1
        #print(X)
        #pca = PCA(n_components=2)
        #a = pca.fit_transform(X)
        #dataSet=list(a)
print(dataSet)
    return dataSet  # dataSet = [[], [], [], ...]
def initCentroids(dataSet, k):
    # 初始化k個質心，隨機獲取
return random.sample(dataSet, k)  # 從dataSet中隨機獲取k個數據項返回
def minDistance(dataSet, centroidList):
    # 對每個屬於dataSet的item，計算item與centroidList中k個質心的歐式距離，找出距離最小的，
    # 並將item加入相應的簇類中
clusterDict = dict()  # 用dict來儲存簇類結果
for item in dataSet:
        vec1 = numpy.array(item)  # 轉換成array形式
flag = 0  # 簇分類標記，記錄與相應簇距離最近的那個簇
minDis = float("inf")  # 初始化為最大值
for i in range(len(centroidList)):
            vec2 = numpy.array(centroidList[i])
            distance = calcuDistance(vec1, vec2)  # 計算相應的歐式距離
if distance < minDis:
                minDis = distance
                flag = i  # 迴圈結束時，flag儲存的是與當前item距離最近的那個簇標記
if flag not in clusterDict.keys():  # 簇標記不存在，進行初始化
clusterDict[flag] = list()
            # print flag, item
clusterDict[flag].append(item)  # 加入相應的類別中
return clusterDict  # 返回新的聚類結果
def getCentroids(clusterDict):
    # 得到k個質心
centroidList = list()
    for key in clusterDict.keys():
        centroid = numpy.mean(numpy.array(clusterDict[key]), axis=0)  # 計算每列的均值，即找到質心
        # print key, centroid
centroidList.append(centroid)
    return numpy.array(centroidList).tolist()

def getVar(clusterDict, centroidList):
    # 計算簇集合間的均方誤差
    # 將簇類中各個向量與質心的距離進行累加求和
sum = 0.0
for key in clusterDict.keys():
        vec1 = numpy.array(centroidList[key])
        distance = 0.0
for item in clusterDict[key]:
            vec2 = numpy.array(item)
            distance += calcuDistance(vec1, vec2)
        sum += distance
    return sum


def showCluster(centroidList, clusterDict):
    # 展示聚類結果
colorMark = ['or', 'ob', 'og', 'ok', 'oy', 'oc','om']  # 不同簇類的標記 'or' --> 'o'代表圓，'r'代表red，'b':blue
centroidMark = ['dr', 'db', 'dg', 'dk', 'dy','oc', 'dm']  # 質心標記 同上'd'代表稜形
for key in clusterDict.keys():
        plt.plot(centroidList[key][0], centroidList[key][1], centroidMark[key], markersize=12)  # 畫質心點
for item in clusterDict[key]:
            plt.plot(item[0], item[1], colorMark[key])  # 畫簇類下的點
plt.show()
if __name__ == '__main__':
    inFile = "jingwei.txt"  # 資料集檔案
dataSet = loadDataSet(inFile)  # 載入資料集
print(dataSet)
    centroidList = initCentroids(dataSet,6)  # 初始化質心，設定k=4
clusterDict = minDistance(dataSet, centroidList)  # 第一次聚類迭代
newVar = getVar(clusterDict, centroidList)  # 獲得均方誤差值，通過新舊均方誤差來獲得迭代終止條件
oldVar = -0.0001  # 舊均方誤差值初始化為-1
print ('***** 第1次迭代 *****')
    print ('簇類')
    for key in clusterDict.keys():
        print(key, ' --> ', clusterDict[key])
    print ('k個均值向量: ', centroidList)
    print ('平均均方誤差: ', newVar)
    print (showCluster(centroidList, clusterDict))  # 展示聚類結果
k = 2
while abs(newVar - oldVar) >= 0.0001:  # 當連續兩次聚類結果小於0.0001時，迭代結束
centroidList = getCentroids(clusterDict)  # 獲得新的質心
clusterDict = minDistance(dataSet, centroidList)  # 新的聚類結果
oldVar = newVar
        newVar = getVar(clusterDict, centroidList)
        print ('***** 第%d次迭代 *****' % k)
        print ('簇類')
        for key in clusterDict.keys():
            print (key, ' --> ', clusterDict[key])
        print ('k個均值向量: ', centroidList)
        print ('平均均方誤差: ', newVar)
        print (showCluster(centroidList, clusterDict) ) # 展示聚類結果
k += 1