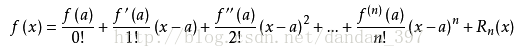Harris角點檢測原理及C++實現

阿新 • • 發佈：2019-01-25

1. 首先，我們不禁要問什麼是harris角點？

對於角點，到目前為止還沒有明確的數學定義。但是你可以認為角點就是極值點，即在某方面屬性特別突出的點。一般的角點檢測都是對有具體定義的、或者是能夠具體檢測出來的興趣點的檢測。這意味著興趣點可以是角點，是在某些屬性上強度最大或者最小的孤立點、線段的終點，或者是曲線上局部曲率最大的點。

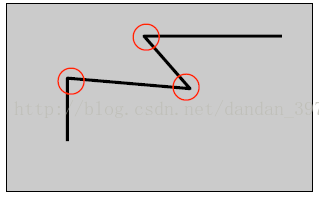
通俗的來說，在一副影象中，我們可以認為角點是物體輪廓線的連線點（見圖1），當拍攝視角變化的時候，這些特徵點仍能很好地保持穩定的屬性。

圖1 corner

角點在保留影象圖形重要特徵的同時，可以有效地減少資訊的資料量，使其資訊的含量很高，有效地提高了計算的速度，有利於影象的可靠匹配，使得實時處理成為可能。它的各種應用，這裡我就不再贅述了。

2. 如何檢測出harris角點？

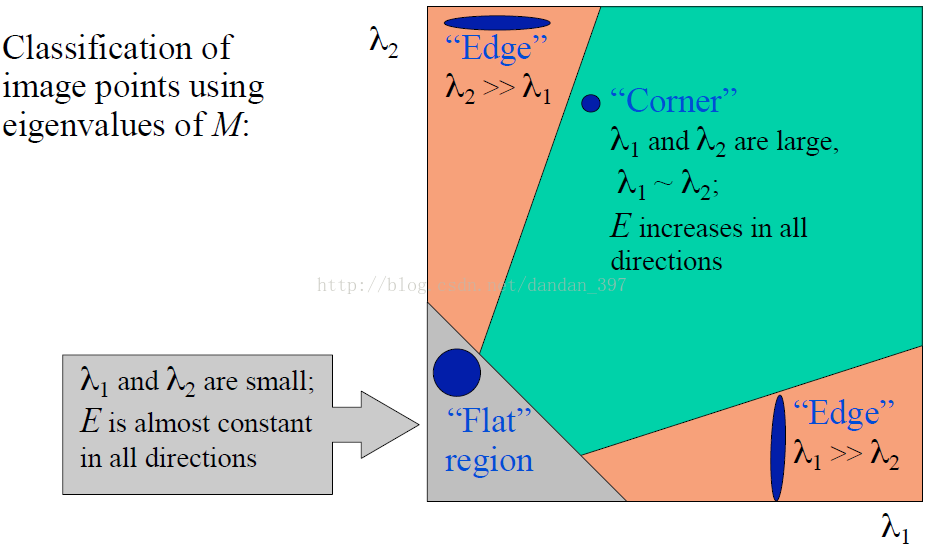
圖2 角點檢測的基本思想

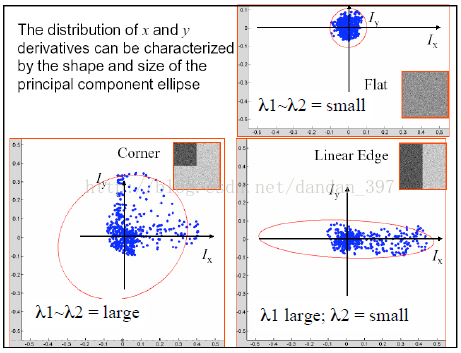
角點檢測最原始的想法就是取某個畫素的一個鄰域視窗，當這個視窗在各個方向上進行小範圍移動時，觀察視窗內平均的畫素灰度值的變化（即，E(u,v)，Window-averaged change of intensity）。從上圖可知，我們可以將一幅影象大致分為三個區域（‘flat’，‘edge’，‘corner’），這三個區域變化是不一樣的。

其中，u,v是視窗在水平，豎直方向的偏移，

這裡可以先簡單複習一下泰勒級數展開的知識，因為馬上就用到啦，

這是一維的情況，對於多元函式，也有類似的泰勒公式。

對I(x+u,y+v)進行二維泰勒級數展開，我們取一階近似，有

圖中藍線圈出的部分我們稱之為結構張量（structure tensor），用M表示。

講到這裡，先明確一點，我們的目的是什麼？我們的目的是尋找這樣的畫素點，它使得我們的u，v無論怎樣取值，E(u,v)都是變化比較大的，這個畫素點就是我們要找的角點。不難觀察，上式近似處理後的E(u,v)是一個二次型，而由下述定理可知，

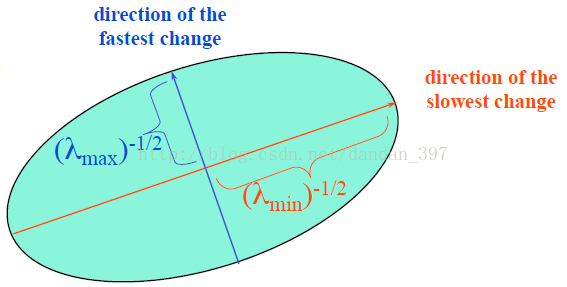
令E(u,v)=常數，我們可用一個橢圓來描繪這一函式。

橢圓的長短軸是與結構張量M的兩個特徵值相對應的量。通過判斷的情況我們就可以區分出‘flat’，‘edge’，‘corner’這三種區域，因為最直觀的印象：

corner：在水平、豎直兩個方向上變化均較大的點，即Ix、Iy都較大；
edge ：僅在水平、或者僅在豎直方向有較大的點，即Ix和Iy只有其一較大；
flat ：在水平、豎直方向的變化量均較小的點，即Ix、Iy都較小；

而結構張量M是由Ix，Iy構成，它的特徵值正好可以反映Ix，Iy的情況，下面我以一種更容易理解的方式來講述橢圓的物理意義。

這樣是不是更清楚了呢^_^......，因此我們可以得出結論：

當然，大牛們並沒有止步於此，這樣通過判斷兩個變數的值來判斷角點畢竟不是很方便。於是他們想出了一種更好的方法，對，就是定義角點響應函式R（corner response function），

針對三種區域，R的取值如何呢？

至此，我們就可以通過判斷R的值來判斷某個點是不是角點了。

角點：R為大數值整數

邊緣：R為大數值負數

平坦區：絕對值R是小數值

3. harris角點檢測演算法步驟

1.利用Soble計算出XY方向的梯度值

2.計算出Ix^2,Iy^2,Ix*Iy

3.利用高斯函式對Ix^2,Iy^2,Ix*Iy進行濾波

4.計算區域性特徵結果矩陣M的特徵值和響應函式C(i,j)=Det(M)-k(trace(M))^2 (0.04<=k<=0.06)

5.將計算出響應函式的值C進行非極大值抑制，濾除一些不是角點的點，同時要滿足大於設定的閾值

下面放上原始碼：

#include "opencv2/imgproc/imgproc.hpp"  
#include "opencv2/highgui/highgui.hpp"  
#include <iostream>  
#include <cmath>
using namespace cv;
using namespace std;
/*
RGB轉換成灰度影象的一個常用公式是：
Gray = R*0.299 + G*0.587 + B*0.114
*/
//******************灰度轉換函式*************************  
//第一個引數image輸入的彩色RGB影象的引用；  
//第二個引數imageGray是轉換後輸出的灰度影象的引用；  
//*******************************************************
void ConvertRGB2GRAY(const Mat &image, Mat &imageGray);

//******************Sobel卷積因子計算X、Y方向梯度和梯度方向角********************  
//第一個引數imageSourc原始灰度影象；  
//第二個引數imageSobelX是X方向梯度影象；  
//第三個引數imageSobelY是Y方向梯度影象；  
//第四個引數pointDrection是梯度方向角陣列指標  
//*************************************************************  
void SobelGradDirction(Mat &imageSource, Mat &imageSobelX, Mat &imageSobelY);

//******************計算Sobel的X方向梯度幅值的平方*************************  
//第一個引數imageGradX是X方向梯度影象；    
//第二個引數SobelAmpXX是輸出的X方向梯度影象的平方  
//*************************************************************  
void SobelXX(const Mat imageGradX, Mat_<float> &SobelAmpXX);

//******************計算Sobel的Y方向梯度幅值的平方*************************    
//第一個引數imageGradY是Y方向梯度影象；  
//第二個引數SobelAmpXX是輸出的Y方向梯度影象的平方  
//*************************************************************  
void SobelYY(const Mat imageGradY, Mat_<float> &SobelAmpYY);

//******************計算Sobel的XY方向梯度幅值的乘積*************************    
//第一個引數imageGradX是X方向梯度影象；
//第二個引數imageGradY是Y方向梯度影象；
//第二個引數SobelAmpXY是輸出的XY方向梯度影象 
//*************************************************************  
void SobelXY(const Mat imageGradX, const Mat imageGradY, Mat_<float> &SobelAmpXY);

//****************計算一維高斯的權值陣列*****************
//第一個引數size是代表的卷積核的邊長的大小
//第二個引數sigma表示的是sigma的大小
//*******************************************************
double *getOneGuassionArray(int size, double sigma);

//****************高斯濾波函式的實現*****************
//第一個引數srcImage是代表的輸入的原圖
//第二個引數dst表示的是輸出的圖
//第三個引數size表示的是卷積核的邊長的大小
//*******************************************************
void MyGaussianBlur(Mat_<float> &srcImage, Mat_<float> &dst, int size);

//****計算區域性特漲結果矩陣M的特徵值和響應函式H = (A*B - C) - k*(A+B)^2******
//M
//A  C
//C  B
//Tr(M)=a+b=A+B
//Det(M)=a*b=A*B-C^2
//計算輸出響應函式的值得矩陣
//****************************************************************************
void harrisResponse(Mat_<float> &GaussXX, Mat_<float> &GaussYY, Mat_<float> &GaussXY, Mat_<float> &resultData,float k);


//***********非極大值抑制和滿足閾值及某鄰域內的區域性極大值為角點**************
//第一個引數是響應函式的矩陣
//第二個引數是輸入的灰度影象
//第三個引數表示的是輸出的角點檢測到的結果圖
void LocalMaxValue(Mat_<float> &resultData, Mat &srcGray, Mat &ResultImage,int kSize);

int main()
{
	const Mat srcImage = imread("3.jpg");
	if (!srcImage.data)
	{
		printf("could not load image...\n");
		return -1;
	}
	imshow("srcImage", srcImage);
	Mat srcGray;
	ConvertRGB2GRAY(srcImage, srcGray);
	Mat imageSobelX;
	Mat imageSobelY;
	Mat resultImage;
	Mat_<float> imageSobelXX;
	Mat_<float> imageSobelYY;
	Mat_<float> imageSobelXY;
	Mat_<float> GaussianXX;
	Mat_<float> GaussianYY;
	Mat_<float> GaussianXY;
	Mat_<float> HarrisRespond;
	//計算Soble的XY梯度
	SobelGradDirction(srcGray, imageSobelX, imageSobelY);
	//計算X方向的梯度的平方
	SobelXX(imageSobelX, imageSobelXX);
	SobelYY(imageSobelY, imageSobelYY);
	SobelXY(imageSobelX, imageSobelY, imageSobelXY);
	//計算高斯模糊XX YY XY
	MyGaussianBlur(imageSobelXX, GaussianXX,3);
	MyGaussianBlur(imageSobelYY, GaussianYY, 3);
	MyGaussianBlur(imageSobelXY, GaussianXY, 3);
	harrisResponse(GaussianXX, GaussianYY, GaussianXY, HarrisRespond, 0.05);
	LocalMaxValue(HarrisRespond, srcGray, resultImage, 3);
	imshow("imageSobelX", imageSobelX);
	imshow("imageSobelY", imageSobelY);
	imshow("resultImage", resultImage);
	waitKey(0);
	return 0;
}
void ConvertRGB2GRAY(const Mat &image, Mat &imageGray)
{
	if (!image.data || image.channels() != 3)
	{
		return;
	}
	//建立一張單通道的灰度影象
	imageGray = Mat::zeros(image.size(), CV_8UC1);
	//取出儲存影象畫素的陣列的指標
	uchar *pointImage = image.data;
	uchar *pointImageGray = imageGray.data;
	//取出影象每行所佔的位元組數
	size_t stepImage = image.step;
	size_t stepImageGray = imageGray.step;
	for (int i = 0; i < imageGray.rows; i++)
	{
		for (int j = 0; j < imageGray.cols; j++)
		{
			pointImageGray[i*stepImageGray + j] = (uchar)(0.114*pointImage[i*stepImage + 3 * j] + 0.587*pointImage[i*stepImage + 3 * j + 1] + 0.299*pointImage[i*stepImage + 3 * j + 2]);
		}
	}
}


//儲存梯度膜長
void SobelGradDirction(Mat &imageSource, Mat &imageSobelX, Mat &imageSobelY)
{
	imageSobelX = Mat::zeros(imageSource.size(), CV_32SC1);
	imageSobelY = Mat::zeros(imageSource.size(), CV_32SC1);
	//取出原圖和X和Y梯度圖的陣列的首地址
	uchar *P = imageSource.data;
	uchar *PX = imageSobelX.data;
	uchar *PY = imageSobelY.data;

	//取出每行所佔據的位元組數
	int step = imageSource.step;
	int stepXY = imageSobelX.step;

	int index = 0;//梯度方向角的索引
	for (int i = 1; i < imageSource.rows - 1; ++i)
	{
		for (int j = 1; j < imageSource.cols - 1; ++j)
		{
			//通過指標遍歷影象上每一個畫素   
			double gradY = P[(i + 1)*step + j - 1] + P[(i + 1)*step + j] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[(i - 1)*step + j] * 2 - P[(i - 1)*step + j + 1];
			PY[i*stepXY + j*(stepXY / step)] = abs(gradY);

			double gradX = P[(i - 1)*step + j + 1] + P[i*step + j + 1] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[i*step + j - 1] * 2 - P[(i + 1)*step + j - 1];
			PX[i*stepXY + j*(stepXY / step)] = abs(gradX);
		}
	}
	//將梯度陣列轉換成8位無符號整型
	convertScaleAbs(imageSobelX, imageSobelX);
	convertScaleAbs(imageSobelY, imageSobelY);
}


void SobelXX(const Mat imageGradX, Mat_<float> &SobelAmpXX)
{
	SobelAmpXX = Mat_<float>(imageGradX.size(), CV_32FC1);
	for (int i = 0; i < SobelAmpXX.rows; i++)
	{
		for (int j = 0; j < SobelAmpXX.cols; j++)
		{
			SobelAmpXX.at<float>(i, j) = imageGradX.at<uchar>(i, j)*imageGradX.at<uchar>(i, j);
		}
	}
	//convertScaleAbs(SobelAmpXX, SobelAmpXX);
}

void SobelYY(const Mat imageGradY, Mat_<float> &SobelAmpYY)
{
	SobelAmpYY = Mat_<float>(imageGradY.size(), CV_32FC1);
	for (int i = 0; i < SobelAmpYY.rows; i++)
	{
		for (int j = 0; j < SobelAmpYY.cols; j++)
		{
			SobelAmpYY.at<float>(i, j) = imageGradY.at<uchar>(i, j)*imageGradY.at<uchar>(i, j);
		}
	}
	//convertScaleAbs(SobelAmpYY, SobelAmpYY);
}

void SobelXY(const Mat imageGradX, const Mat imageGradY, Mat_<float> &SobelAmpXY)
{
	SobelAmpXY = Mat_<float>(imageGradX.size(), CV_32FC1);
	for (int i = 0; i < SobelAmpXY.rows; i++)
	{
		for (int j = 0; j < SobelAmpXY.cols; j++)
		{
			SobelAmpXY.at<float>(i, j) = imageGradX.at<uchar>(i, j)*imageGradY.at<uchar>(i, j);
		}
	}
	//convertScaleAbs(SobelAmpXY, SobelAmpXY);
}



//計算一維高斯的權值陣列
double *getOneGuassionArray(int size, double sigma)
{
	double sum = 0.0;
	//定義高斯核半徑
	int kerR = size / 2;

	//建立一個size大小的動態一維陣列
	double *arr = new double[size];
	for (int i = 0; i < size; i++)
	{

		// 高斯函式前的常數可以不用計算，會在歸一化的過程中給消去
		arr[i] = exp(-((i - kerR)*(i - kerR)) / (2 * sigma*sigma));
		sum += arr[i];//將所有的值進行相加

	}
	//進行歸一化	
	for (int i = 0; i < size; i++)
	{
		arr[i] /= sum;
		cout << arr[i] << endl;
	}
	return arr;
}

void MyGaussianBlur(Mat_<float> &srcImage, Mat_<float> &dst, int size)
{
	CV_Assert(srcImage.channels() == 1 || srcImage.channels() == 3); // 只處理單通道或者三通道影象
	int kerR = size / 2;
	dst = srcImage.clone();
	int channels = dst.channels();
	double* arr;
	arr = getOneGuassionArray(size, 1);//先求出高斯陣列

									   //遍歷影象 水平方向的卷積
	for (int i = kerR; i < dst.rows - kerR; i++)
	{
		for (int j = kerR; j < dst.cols - kerR; j++)
		{
			float GuassionSum[3] = { 0 };
			//滑窗搜尋完成高斯核平滑
			for (int k = -kerR; k <= kerR; k++)
			{

				if (channels == 1)//如果只是單通道
				{
					GuassionSum[0] += arr[kerR + k] * dst.at<float>(i, j + k);//行不變，列變換，先做水平方向的卷積
				}
				else if (channels == 3)//如果是三通道的情況
				{
					Vec3f bgr = dst.at<Vec3f>(i, j + k);
					auto a = arr[kerR + k];
					GuassionSum[0] += a*bgr[0];
					GuassionSum[1] += a*bgr[1];
					GuassionSum[2] += a*bgr[2];
				}
			}
			for (int k = 0; k < channels; k++)
			{
				if (GuassionSum[k] < 0)
					GuassionSum[k] = 0;
				else if (GuassionSum[k] > 255)
					GuassionSum[k] = 255;
			}
			if (channels == 1)
				dst.at<float>(i, j) = static_cast<float>(GuassionSum[0]);
			else if (channels == 3)
			{
				Vec3f bgr = { static_cast<float>(GuassionSum[0]), static_cast<float>(GuassionSum[1]), static_cast<float>(GuassionSum[2]) };
				dst.at<Vec3f>(i, j) = bgr;
			}

		}
	}

	//豎直方向
	for (int i = kerR; i < dst.rows - kerR; i++)
	{
		for (int j = kerR; j < dst.cols - kerR; j++)
		{
			float GuassionSum[3] = { 0 };
			//滑窗搜尋完成高斯核平滑
			for (int k = -kerR; k <= kerR; k++)
			{

				if (channels == 1)//如果只是單通道
				{
					GuassionSum[0] += arr[kerR + k] * dst.at<float>(i + k, j);//行變，列不換，再做豎直方向的卷積
				}
				else if (channels == 3)//如果是三通道的情況
				{
					Vec3f bgr = dst.at<Vec3f>(i + k, j);
					auto a = arr[kerR + k];
					GuassionSum[0] += a*bgr[0];
					GuassionSum[1] += a*bgr[1];
					GuassionSum[2] += a*bgr[2];
				}
			}
			for (int k = 0; k < channels; k++)
			{
				if (GuassionSum[k] < 0)
					GuassionSum[k] = 0;
				else if (GuassionSum[k] > 255)
					GuassionSum[k] = 255;
			}
			if (channels == 1)
				dst.at<float>(i, j) = static_cast<float>(GuassionSum[0]);
			else if (channels == 3)
			{
				Vec3f bgr = { static_cast<float>(GuassionSum[0]), static_cast<float>(GuassionSum[1]), static_cast<float>(GuassionSum[2]) };
				dst.at<Vec3f>(i, j) = bgr;
			}

		}
	}
	delete[] arr;
}

void harrisResponse(Mat_<float> &GaussXX, Mat_<float> &GaussYY, Mat_<float> &GaussXY, Mat_<float> &resultData,float k)
{
	//建立一張響應函式輸出的矩陣
	resultData = Mat_<float>(GaussXX.size(), CV_32FC1);
	for (int i = 0; i < resultData.rows; i++)
	{
		for (int j = 0; j < resultData.cols; j++)
		{
			float a = GaussXX.at<float>(i, j);
			float b = GaussYY.at<float>(i, j);
			float c = GaussXY.at<float>(i, j);
			resultData.at<float>(i, j) = a*b - c*c - k*(a + b)*(a + b);
		}
	}
}


//非極大值抑制
void LocalMaxValue(Mat_<float> &resultData, Mat &srcGray, Mat &ResultImage, int kSize)
{
	int r = kSize / 2;
	ResultImage = srcGray.clone();
	for (int i = r; i < ResultImage.rows - r; i++)
	{
		for (int j = r; j < ResultImage.cols - r; j++)
		{
			if (resultData.at<float>(i, j) > resultData.at<float>(i - 1, j - 1) &&
				resultData.at<float>(i, j) > resultData.at<float>(i - 1, j) &&
				resultData.at<float>(i, j) > resultData.at<float>(i - 1, j - 1) &&
				resultData.at<float>(i, j) > resultData.at<float>(i - 1, j + 1) &&
				resultData.at<float>(i, j) > resultData.at<float>(i, j - 1) &&
				resultData.at<float>(i, j) > resultData.at<float>(i, j + 1) &&
				resultData.at<float>(i, j) > resultData.at<float>(i + 1, j - 1) &&
				resultData.at<float>(i, j) > resultData.at<float>(i + 1, j) &&
				resultData.at<float>(i, j) > resultData.at<float>(i + 1, j + 1))
			{
				if ((int)resultData.at<float>(i, j) > 18000)
				{
					circle(ResultImage, Point(i, j), 5, Scalar(0,0,255), 2, 8, 0);
				}
			}

		}
	}
}

Harris角點檢測原理及C++實現

Harris角點檢測原理及C++實現

Harris角點檢測原理及實現

Harris角點檢測原理與opencv（python）實現

第十一節、Harris角點檢測原理

Harris角點檢測原理

Harris角點檢測原理分析

Harris角點檢測原理詳解外加原始碼分析

第十一節、Harris角點檢測原理(附原始碼)

Canny邊緣檢測原理及C++實現

Harris角點檢測的實現（cv::Mat && c++）

OpenCv-C++-Harris角點檢測

Harris角點提取演算法及實現

Python 實現Harris 角點檢測

Harris角點檢測實現詳解

Harris角點檢測及matlab程式

Harris角點檢測及程式碼分析（續）

opencv-角點檢測之Harris角點檢測

Opencv Harris角點檢測

LBP特徵原理及C實現

影象插值演算法的原理及C++實現

Harris角點檢測原理及C++實現

相關推薦