Introduction

凸包（Convex Hull）是計算幾何中的一類極其重要的問題，計算幾何中的很多問題都可以轉化為凸包問題來解決。

直觀的來講，凸包就像是在一塊釘有若干個釘子的木板上撐開一根橡皮筋來講所有釘子圍起來一樣。

這裡寫圖片描述

構造凸包的演算法可謂汗牛充棟，著名的有Gift wrapping（Jarvis March演算法）, Graham scan, QuickHull, Divide and conquer, Incremental convex hull algorithm等。本文不可能面面俱到，在這裡只選取一些具有代表性的演算法來闡釋凸包構造過程中的基本思想。

下面所介紹的演算法中基本上都體現出了一個特徵，就是利用問題的集合特質將問題一步步的轉化，大事化小，小事化了，從而使問題得到解決。

基於極點的演算法

極點

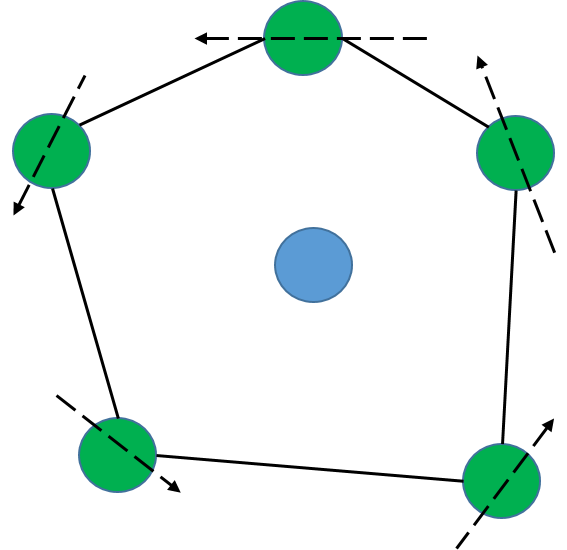
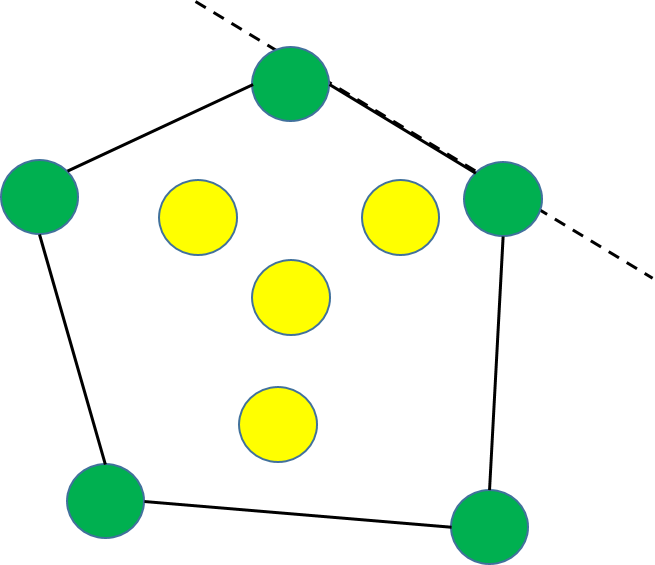
設S為平面點集，若存在一條經過點p的直線l使得除p點外所有的點都位於直線l的同一端，那麼稱點p為極點（Extreme Point）。否則稱為非極點（Non-Extreme Point）。

這裡寫圖片描述

如上圖所示，直觀的來講，一個點是極點那麼它一定就是凸包上的點。

構造策略

回憶一下氣泡排序的原理：

一個序列有序當且僅當每一個點都是有序的

同樣的根據極點的概念我們有如下的凸包定義：

一個多邊形為凸包當且僅當所有頂點都是極點

根據極點的定義我們可以想出一個很直接的凸包的構造演算法：遍歷每個點，檢查是否為極點，如果是，就將它加入到凸包的集合中。

這樣，構造凸包的問題就被我們轉化為了判斷點是否為極點的問題，雖然離我們的目標還有一些距離，但已經前進了一大步。不過，我們還沒有判斷極點的演算法。

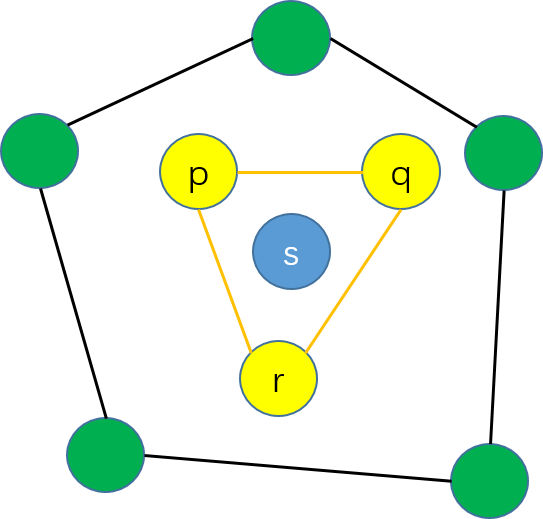
這裡寫圖片描述

要判斷一個點是不是極點其實很容易，它要不是極點，那麼一定能找到三個點（從給定的點集中）將它包圍起來。原因很簡單，因為平面點集的凸包就是能將所有點包圍起來的凸多邊形，那麼對於在凸包內部的點（不是極點的點）最少最少能從凸包上找到三個點將其圍起來。於是就有：

平面點集S中的一個點s不是極點當且僅當存在{p,q,r}⊆S∖{s}使得s∈△(p,q,r)，其中△(p,q,r)代表p,q,r⊆S組成的封閉三角形。

In-Triangle Test

雖然有了上面的判斷極點的In-Triangle Test方法，但我們還無法馬上給出一個實現，因為我們還不知道如何判斷點是不是在三角形內。

要判斷點是否在三角形內，需要用到一個計算幾何中十分常用而重要的技術，叫做To-Left測試。

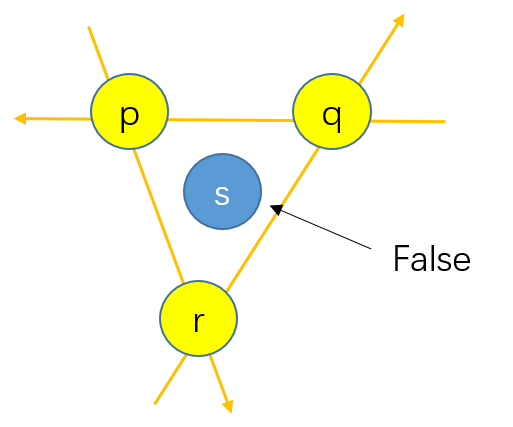
這裡寫圖片描述

觀察上面的圖片，如果我們按照一定的順序（如順時針）檢查三個點p,q,r構成的有向線段，就會發現無論是對於有向線段rq還是qp和pr，點s都位於它們的左邊。

To-Left測試則可以完成這樣的任務，對於點(a,b,s)，當s位於有向線段ab的左側時，ToLeft(a, b, s)返回True，否則返回False。其利用的原理是叉積。

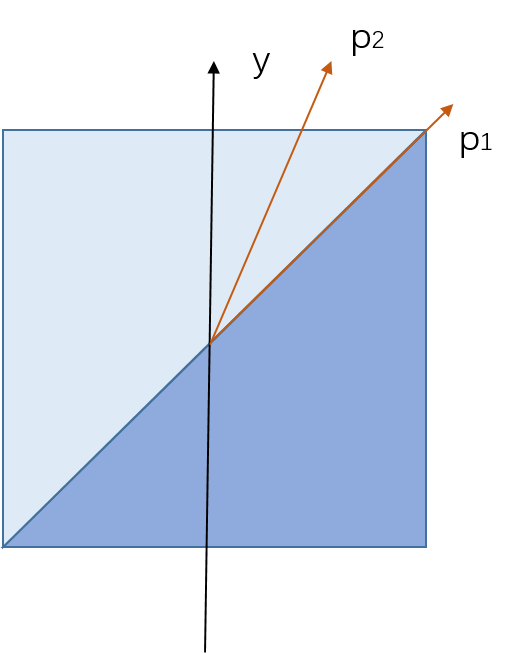
叉積（又稱外積），其集合意義是向量p1→和p2→構成的平行四邊形的有向面積。同時，當p1→×p2→>0時，p1→位於p2→的順時針方向，反之p1→位於p2→的逆時針方向。

這裡寫圖片描述

我們現在可以給出To-Left測試的實現：

bool ToLeft(Point p, Point q, Point s){
    return p.x * q.y - p.y * q.x
        + q.x * s.y - q.y * s.x
        + s.x * p.y - s.y * p.x > 0;
}

完整演算法

下面我們可以給出這個演算法的完整實現：

mark all points of S as Extreme;

for each triangle(p,q,r):
    for each point s except (p,q,r):
        if s lies inside triangle(p,q,r):
            mark s as Non-Extreme;

列舉每個三角形需要O(n3)的時間，加上對每個三角形列舉每個點該演算法總的時間複雜度為O(n4)。

基於極邊的演算法

剛才我們得到了一個可用的演算法，但這近乎於brute-force，演算法的時間複雜度過高以致於幾乎不能用，為此我們不得不考慮更優的演算法。

論及上面那個演算法為什麼這麼慢的話，其原因便在於我們是基於極點來構造凸包的，而要判斷極點又不得不列舉所有三角形，這樣複雜度一下子就上去了，於是我們只有繼續發掘看看凸包的幾何性質，來找到一種更好的方法。

極邊

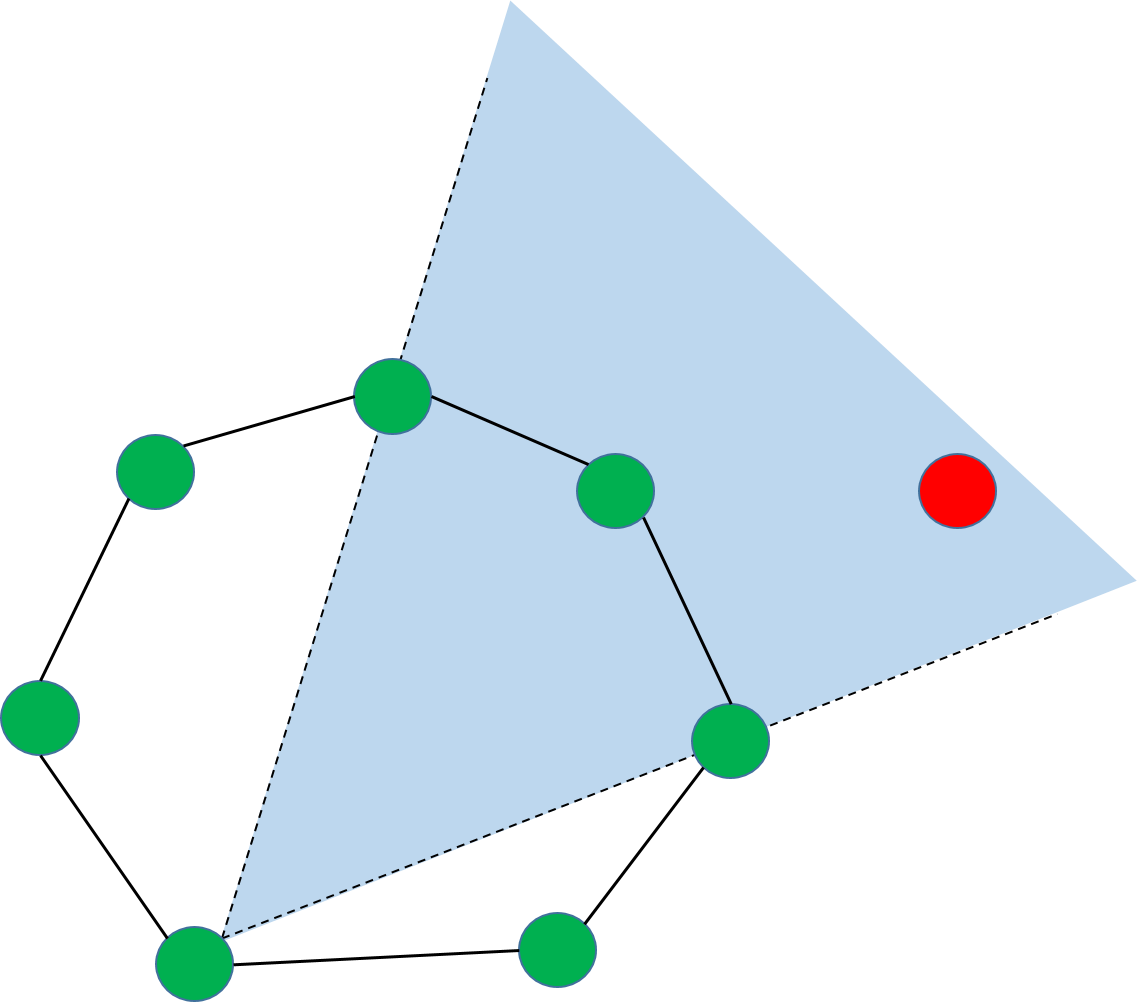
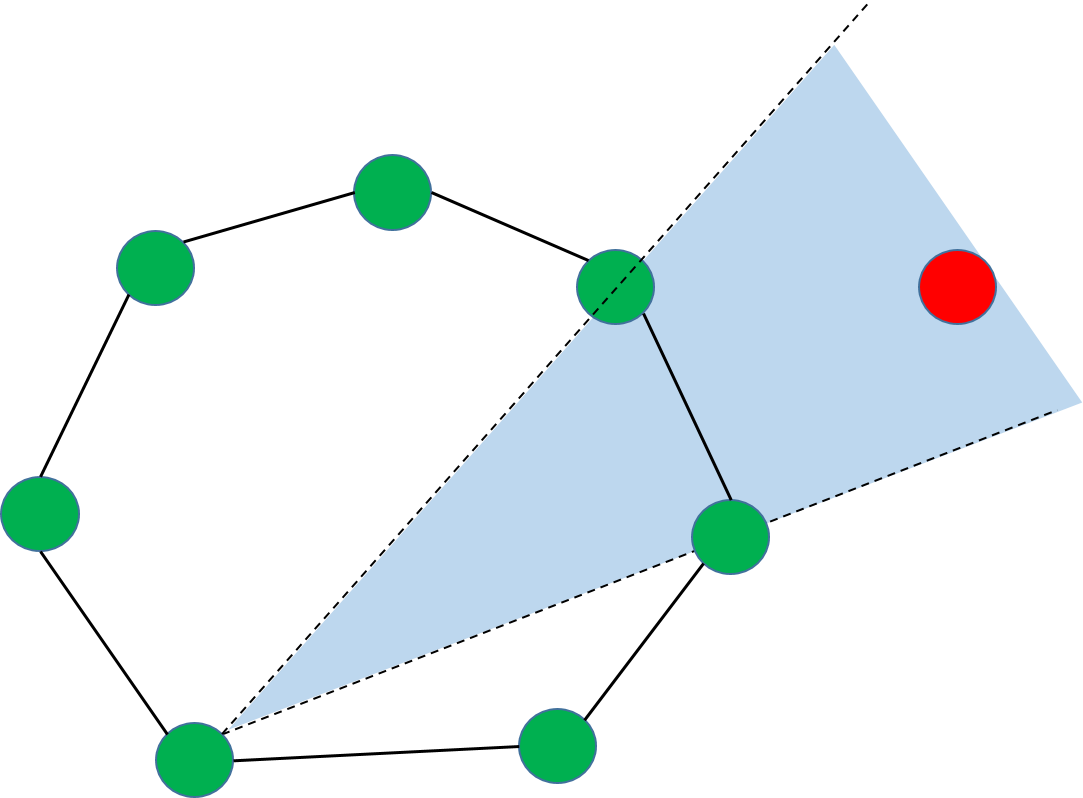
這裡寫圖片描述

觀察上圖就可以發現，對於凸包上的每一條邊，都將平面分成了兩部分，並且其它所有的點都位於這條邊的一側。這些邊稱為極邊。

對於s,t∈S,e=(s,t)為一條極邊當且僅當S∖{s,t}中所有的點都位於e的同一側。

根據上一節的經驗，我們不難得出判斷極邊的方法：只要對每一個點進行一次To-Left測試即可。

完整演算法

根據上面極邊的定義我們可以將構造凸包的任務轉化為判斷極邊。這樣我們只需要遍歷每一條邊，然後檢查它是否是極邊即可。

下面是完整演算法的虛擬碼：

let set of Extreme Edges empty;

for each segment pq:
    if points in S \ {p, q} lies to the same side of pq:
        then add pq to set of Extreme Edges;

按照上面的演算法，列舉每條邊需要O(n2)的時間，再對每個點進行檢查總共的時間複雜度為O(n3)。

和上面的演算法一樣，這個演算法的核心也是To-Left測試，只不過複雜度大大的下降了，這是一個長足的進步。

增量構造法 Incremental Construction

我們已經給出了兩個演算法，然而在實際應用中這兩個演算法的表現都不能讓人滿意。

在計算幾何中常常會用到一種增量構造的技術，用增量法求凸包的思想是逐次的將點加入到凸包中，最終得到完整的凸包。這個演算法的複雜度為O(n2)。

與插入排序類比

為了更好的理解這個演算法，我們來回憶一下插入排序的原理。

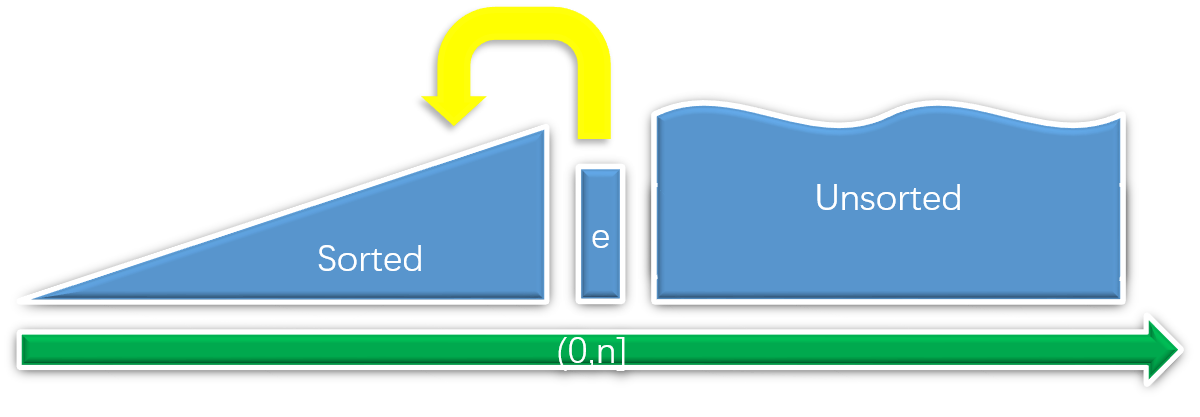
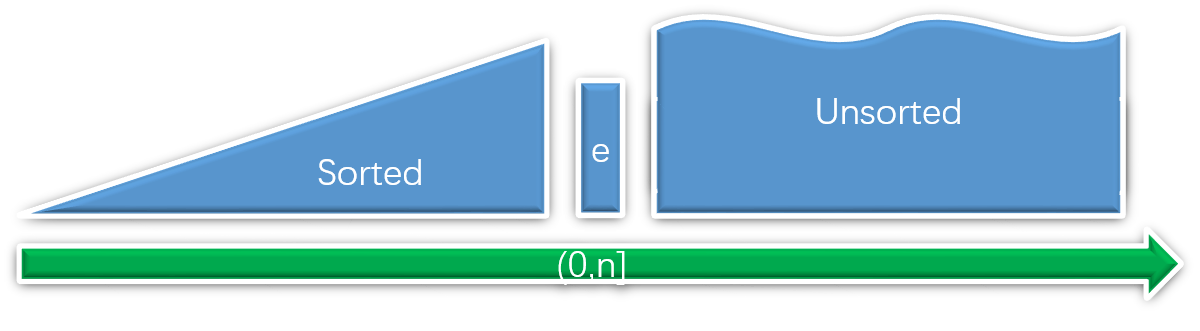
插入排序：不斷地從未排序的元素中一個一個地取出元素插入到有序的序列中來構造有序序列

這裡寫圖片描述

增量法就是從未檢查的點中，每次取出一個點，檢查它是否應該被加入到凸包中。

增量法：不斷地地從未檢查的點中一個一個地取出點加入到凸包中

這裡寫圖片描述

不過，和插入排序不同的是，插入排序中有序序列只增不減，而凸包的增量法中有可能會出現以前被判定為凸包的點中在後來發現不屬於凸包的情況，也就是說有增有減，如上圖所示的情況。

要實現增量法，我們需要清楚兩件事：

如何判斷點是否在凸包（凸多邊形）內
如何將新的點與已有凸包合併

我們先來討論第一個問題。

In-Polygon Test(Binary Search)

據說判斷點在凸多邊形內是一道面試題，而且這個問題有一個O(logn)的演算法，就是用二分法。

也許你會感到詫異，不過看了下面的圖你應該就會明白。

這裡寫圖片描述

如果我們給凸多邊形上所有的點從0−n依次標上序號（逆時針），然後以0,n/2為有向線段對點s做To-Left測試，看點s落在有向線段的左邊還是右邊。

這裡寫圖片描述

假設是右邊，那我們再二分取0,n/4進行To-Left測試。

這裡寫圖片描述

直到我們將範圍縮小到點在0,i和0,i+1這兩條有向線段之間的情況，那麼我們只需要對i,i+1和點s做To-Left測試，就能判斷點是否在凸多邊形內了。由於用了二分法，每次判定都會收縮一半，所以可以在O(logn)的時間內完成。

這個演算法看起來很美好不是嗎？不過它並不適用於當前的情況。

這裡寫圖片描述

想想插入排序，你可能注意到可以對有序的部分用二分法，這樣我們就可以在O(logn)的時間內確定新元素在有序序列中的位置了，而無需花O(n)的時間來一個一個找了。

不過這個想法有個致命的錯誤就是運用二分法的前提是我們得使用支援”按秩查詢”的資料結構，如陣列，然而這種資料結構的一個特點是插入十分低效。為了插入一個元素，我們不得不將後面所有元素都向後挪一位，這樣最壞情況下時間複雜度高達O(n)。

所以說，即使你用O(logn)的時間進行定位，然而卻不得不花O(n)的時間來插入，如果我們按一個一個找的方式來定位，並在找的過程中不斷交換元素次序，這樣的時間複雜度也是O(n)，而且實際表現可能比二分+插入更好。

同理，在構造凸包的過程中，若我們二分法判定一個點應當屬於凸包後，我們將在插入點的過程中耗費大量時間，所以這種方法只適用於靜態判斷，對於動態的構造過程並不適用。

In-Polygon Test(Dynamically)

在上面的方法失敗後，我們需要找到一種新的方法。

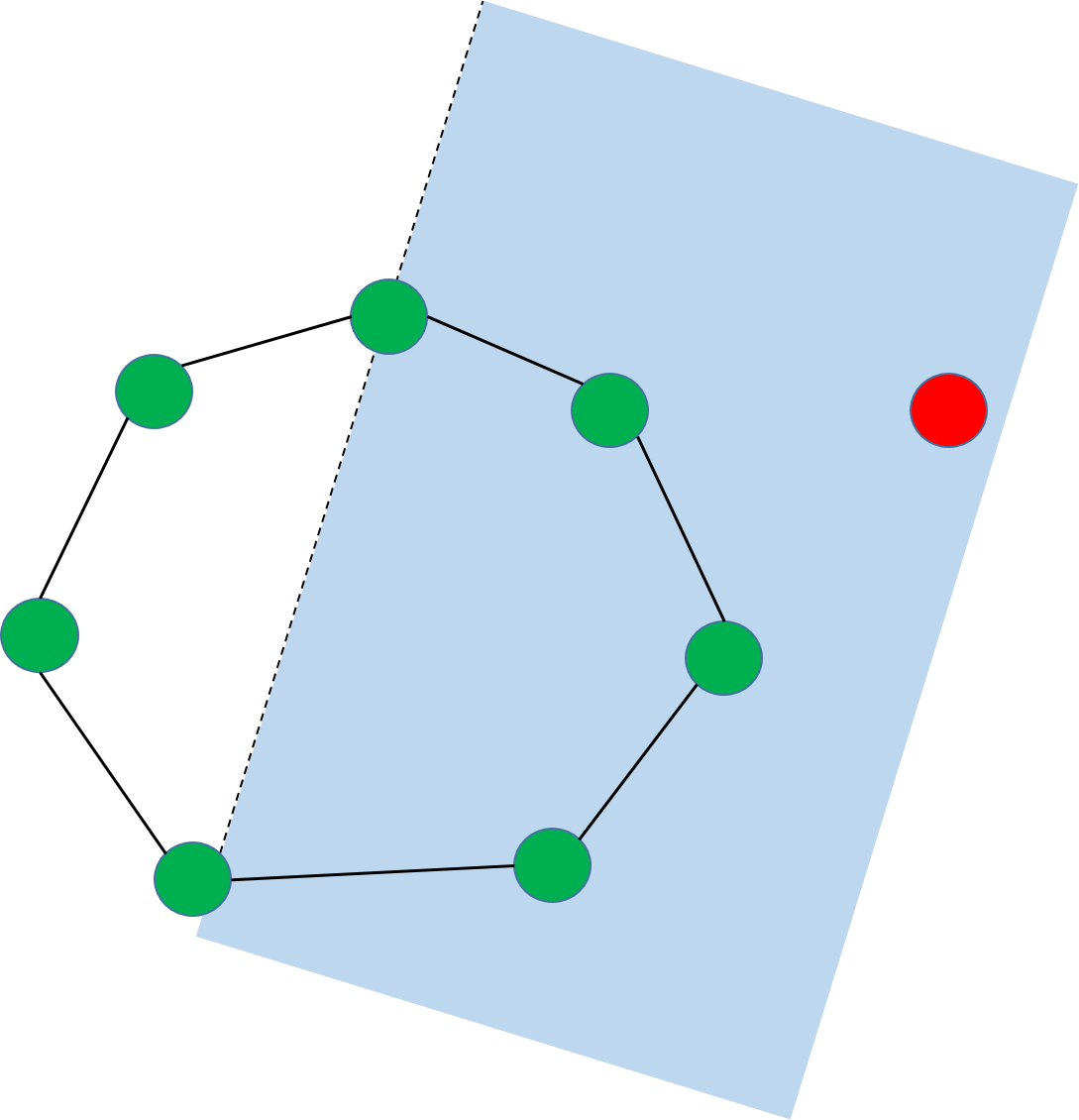
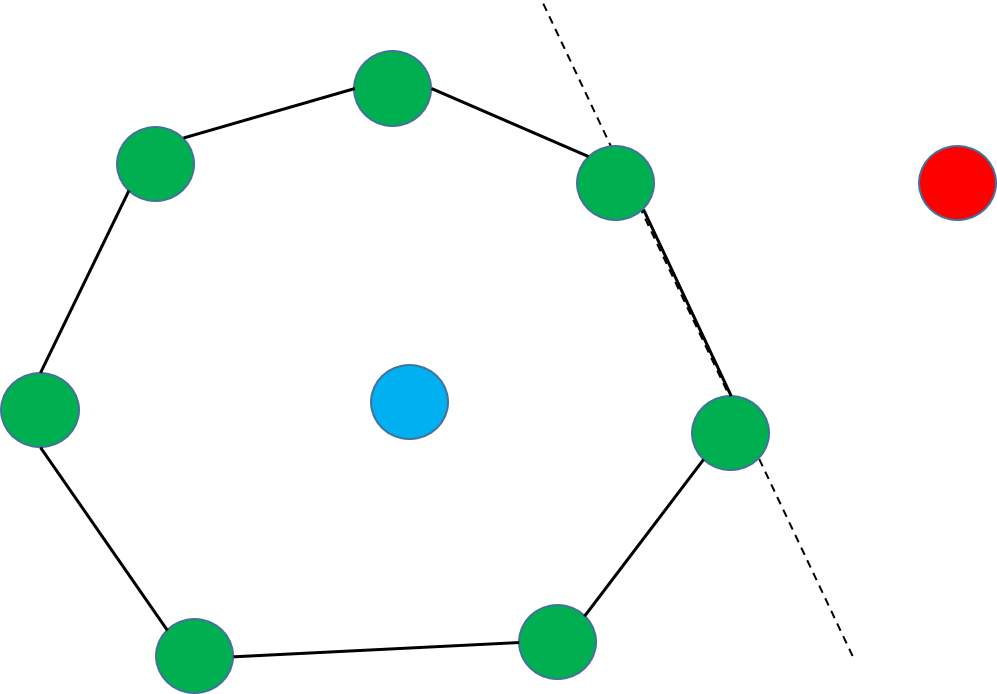
這裡寫圖片描述

實際上，只要我們細心觀察就會發現，如果一個點位於凸包的內部，那麼我們按一定方向遍歷每條邊對點進行To-Left測試都會返回同樣的結果，也就是說位於每條邊的同一側，而在外部的話至少會有一次To-Left測試返回不同的結果。

所以，判斷點在凸多邊形內最終歸約為n次To-Left測試。

加入新的極點

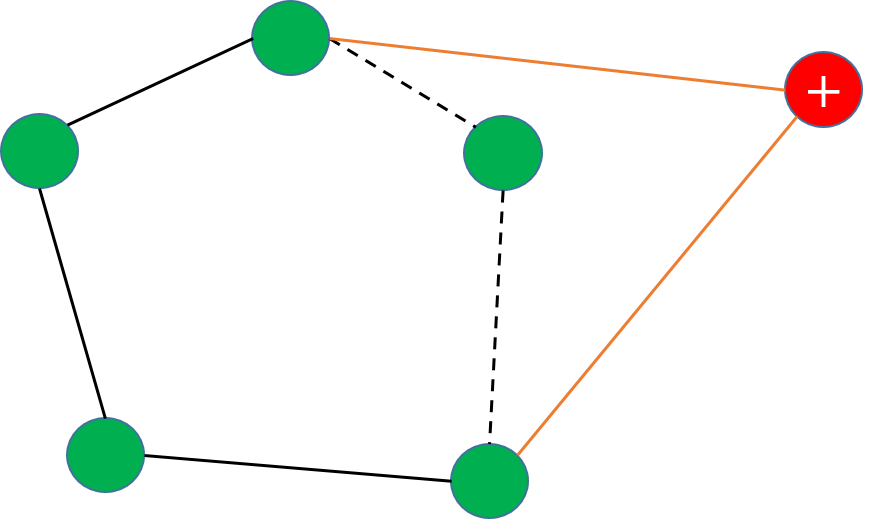
若點再多邊形內部，我們直接捨棄這個點就行了，但若在多邊形外部，我們就需要考慮如何將點加入到現有的凸包中。

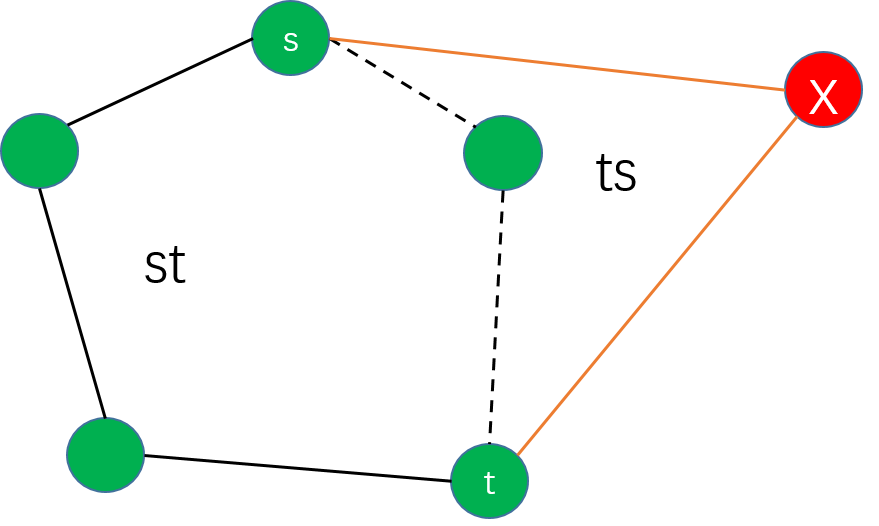
這裡寫圖片描述

從上面的圖可以看出，當我們需要加入新的極點時，這個點會與凸包有兩條切線，兩個切點我們稱為t,s，兩條切線之間的那些邊（稱作ts）需要被剔除，而其他的（稱作st）則需保留。

如果我們需要找出哪些點需要被刪除時，那隻需要找到兩個切點即可。

注意觀察凸包上某一點

演算法學習筆記之計算幾何--平面凸包

Introduction

基於極點的演算法

極點

構造策略

In-Triangle Test

完整演算法

基於極邊的演算法

極邊

完整演算法

增量構造法 Incremental Construction

與插入排序類比

In-Polygon Test(Binary Search)

In-Polygon Test(Dynamically)

加入新的極點

演算法學習筆記之計算幾何--平面凸包

計算幾何：凸包學習筆記 --- Graham 掃描法

20170721 PyTorch學習筆記之計算圖

nBodyCS<I>學習筆記之計算著色器

【學習筆記：計算幾何基礎3】 Convex Hull

【學習筆記：計算幾何基礎4】 Geometric Intersection

【學習筆記：計算幾何基礎5】 Triangulation

資料結構與演算法學習筆記之後進先出的“桶”

演算法學習筆記之——priority queue、heapsort、symbol table、binary search trees

資料結構與演算法學習筆記之複雜度分析

資料結構與演算法學習筆記之提高讀取效能的連結串列（上）

資料結構與演算法學習筆記之先進先出的佇列

資料結構與演算法學習筆記之高效、簡潔的編碼技巧“遞迴”

資料結構與演算法學習筆記之如何分析一個排序演算法？

資料結構與演算法學習筆記之適合大規模的資料排序

資料結構與演算法學習筆記之為用於高考名次排序的排序演算法

演算法學習筆記之遞推演算法

演算法學習筆記之遞迴演算法

演算法學習筆記之分治演算法

演算法學習筆記之百錢買百雞問題

演算法學習筆記之計算幾何--平面凸包

Introduction

基於極點的演算法

極點

構造策略

In-Triangle Test

完整演算法

基於極邊的演算法

極邊

完整演算法

增量構造法 Incremental Construction

與插入排序類比

In-Polygon Test(Binary Search)

In-Polygon Test(Dynamically)

加入新的極點

相關推薦