Description

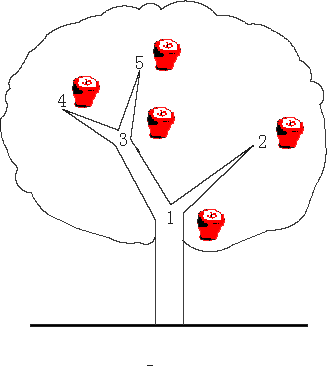
There is an apple tree outside of kaka’s house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won’t grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input

The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
“C x” which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
“Q x” which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning

Output

For every inquiry, output the correspond answer per line.
Sample Input

3
1 2
1 3
3
Q 1
C 2
Q 1
Sample Output

3
2

一棵蘋果樹，樹上的每個分叉和端點都會長蘋果，現有兩種操作
C操作是將某個分叉點或端點的蘋果摘下或長出來，取決於該操作前這個位置是否有蘋果，初始時所有節點都有蘋果。
Q操作是詢問某個分叉點的子樹一共有多少個蘋果

通過深搜為每個節點賦上初始和結束兩個標號，這個編號就相當於轄區，代表這個節點之下的節點們在這個範圍之內，也就是整個子樹的範圍。假設某個節點的初始和結束標號分別為a,b，則這個範圍內擁有的蘋果總數就是[1,b]-[1,a-1]，至於怎麼維護這個區間就要用樹狀陣列了

#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include <queue>
#include <cstdio>
#include <set>
#include <math.h>
#include <algorithm>
#include <queue>
#include <iomanip>
#include <ctime>
#define INF 0x3f3f3f3f
#define MAXN 500005
#define Mod 1000000007
using namespace std;
struct Node
{
    int to,next;
} edge[MAXN<<2];
int n,c[MAXN],head[MAXN],e,cnt;
int st[MAXN],en[MAXN],vis[MAXN],have[MAXN];
int lowbit(int x)
{
    return x&(-x);
}
int sum(int x)
{
    int ans=0;
    for(; x>0; x-=lowbit(x))
        ans+=c[x];
    return ans;
}
void add(int x,int num)
{
    for(; x<=n; x+=lowbit(x))
        c[x]+=num;
}
void addedge(int u,int v)
{
    edge[e].to=v;
    edge[e].next=head[u];
    head[u]=e++;
}
void dfs(int u)
{
    cnt++;
    st[u]=cnt;
    vis[u]=1;
    for(int i=head[u]; i!=-1; i=edge[i].next)
    {
        int v=edge[i].to;
        if(!vis[v])
            dfs(v);
    }
    en[u]=cnt;
}
int main()
{
    while(~scanf("%d",&n))
    {
        e=0;
        cnt=0;
        memset(c,0,sizeof(c));
        memset(head,-1,sizeof(head));
        memset(vis,0,sizeof(vis));
        int u,v;
        for(int i=1; i<n; ++i)
        {
            scanf("%d%d",&u,&v);
            addedge(u,v);
            addedge(v,u);
        }
        dfs(1);
        for(int i=1; i<=n; ++i)
        {
            add(i,1);
            have[i]=1;
        }
        int m,x;
        scanf("%d",&m);
        while(m--)
        {
            char op;
            cin>>op;
            if(op=='C')
            {
                scanf("%d",&x);
                if(have[x])
                {
                    add(st[x],-1);
                    have[x]=0;
                }
                else
                {
                    add(st[x],1);
                    have[x]=1;
                }
            }
            else
            {
                scanf("%d",&x);
                printf("%d\n",sum(en[x])-sum(st[x]-1));
            }
        }
    }
    return 0;
}