資料庫索引的設計原理以及意義

阿新 • • 發佈：2019-01-26

本文內容主要來源於網際網路上主流文章，只是按照個人理解稍作整合，後面附有參考連結。

一、摘要

本文以MySQL資料庫為研究物件，討論與資料庫索引相關的一些話題。特別需要說明的是，MySQL支援諸多儲存引擎，而各種儲存引擎對索引的支援也各不相同，因此MySQL資料庫支援多種索引型別，如BTree索引，雜湊索引，全文索引等等。為了避免混亂，本文將只關注於BTree索引，因為這是平常使用MySQL時主要打交道的索引，至於雜湊索引和全文索引本文暫不討論。

二、常見的查詢演算法及資料結構

為什麼這裡要講查詢演算法和資料結構呢？因為之所以要建立索引，其實就是為了構建一種資料結構，可以在上面應用一種高效的查詢演算法，最終提高資料的查詢速度。

2.1 索引的本質

MySQL官方對索引的定義為：索引（Index）是幫助MySQL高效獲取資料的資料結構。提取句子主幹，就可以得到索引的本質：索引是資料結構。

2.2 常見的查詢演算法

我們知道，資料庫查詢是資料庫的最主要功能之一。我們都希望查詢資料的速度能儘可能的快，因此資料庫系統的設計者會從查詢演算法的角度進行優化。那麼有哪些查詢演算法可以使查詢速度變得更快呢？

2.2.1 順序查詢（linear search ）

最基本的查詢演算法當然是順序查詢（linear search），也就是對比每個元素的方法，不過這種演算法在資料量很大時效率是極低的。
資料結構：有序或無序佇列
複雜度：O(n)

例項程式碼：

//順序查詢
int SequenceSearch(int a[], int value, int n)
{
    int i;
    for(i=0; i<n; i++)
        if(a[i]==value)
            return i;
    return -1;
}

2.2.2 二分查詢（binary search）

比順序查詢更快的查詢方法應該就是二分查找了，二分查詢的原理是查詢過程從陣列的中間元素開始，如果中間元素正好是要查詢的元素，則搜素過程結束；如果某一特定元素大於或者小於中間元素，則在陣列大於或小於中間元素的那一半中查詢，而且跟開始一樣從中間元素開始比較。如果在某一步驟陣列為空，則代表找不到。
資料結構：有序陣列
複雜度：O(logn)

例項程式碼：

//二分查詢，遞迴版本
int BinarySearch2(int a[], int value, int low, int high)
{
    int mid = low+(high-low)/2;
    if(a[mid]==value)
        return mid;
    if(a[mid]>value)
        return BinarySearch2(a, value, low, mid-1);
    if(a[mid]<value)
        return BinarySearch2(a, value, mid+1, high);
}

2.2.3 二叉排序樹查詢

二叉排序樹的特點是：

若它的左子樹不空，則左子樹上所有結點的值均小於它的根結點的值；
若它的右子樹不空，則右子樹上所有結點的值均大於它的根結點的值；
它的左、右子樹也分別為二叉排序樹。

搜尋的原理：

若b是空樹，則搜尋失敗，否則：
若x等於b的根節點的資料域之值，則查詢成功；否則：
若x小於b的根節點的資料域之值，則搜尋左子樹；否則：
查詢右子樹。

資料結構：二叉排序樹
時間複雜度： O(log2N)

2.2.4 雜湊雜湊法(雜湊表)

其原理是首先根據key值和雜湊函式建立一個雜湊表（散列表），燃耗根據鍵值，通過雜湊函式，定位資料元素位置。

資料結構：雜湊表
時間複雜度：幾乎是O(1)，取決於產生衝突的多少。

2.2.5 分塊查詢

分塊查詢又稱索引順序查詢，它是順序查詢的一種改進方法。其演算法思想是將n個數據元素”按塊有序”劃分為m塊（m ≤ n）。每一塊中的結點不必有序，但塊與塊之間必須”按塊有序”；即第1塊中任一元素的關鍵字都必須小於第2塊中任一元素的關鍵字；而第2塊中任一元素又都必須小於第3塊中的任一元素，依次類推。
　　
演算法流程：

先選取各塊中的最大關鍵字構成一個索引表；
查詢分兩個部分：先對索引表進行二分查詢或順序查詢，以確定待查記錄在哪一塊中；然後，在已確定的塊中用順序法進行查詢。

這種搜尋演算法每一次比較都使搜尋範圍縮小一半。它們的查詢速度就有了很大的提升，複雜度為。如果稍微分析一下會發現，每種查詢演算法都只能應用於特定的資料結構之上，例如二分查詢要求被檢索資料有序，而二叉樹查詢只能應用於二叉查詢樹上，但是資料本身的組織結構不可能完全滿足各種資料結構（例如，理論上不可能同時將兩列都按順序進行組織），所以，在資料之外，資料庫系統還維護著滿足特定查詢演算法的資料結構，這些資料結構以某種方式引用（指向）資料，這樣就可以在這些資料結構上實現高階查詢演算法。這種資料結構，就是索引。

2.3 平衡多路搜尋樹B樹（B-tree）

上面講到了二叉樹，它的搜尋時間複雜度為O(log2N)，所以它的搜尋效率和樹的深度有關，如果要提高查詢速度，那麼就要降低樹的深度。要降低樹的深度，很自然的方法就是採用多叉樹，再結合平衡二叉樹的思想，我們可以構建一個平衡多叉樹結構，然後就可以在上面構建平衡多路查詢演算法，提高大資料量下的搜尋效率。

2.3.1 B Tree

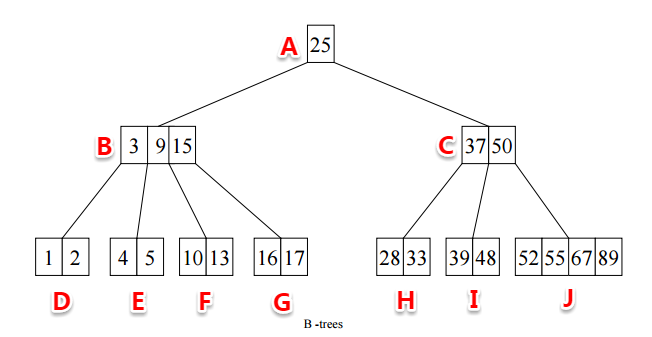
B樹（Balance Tree）又叫做B- 樹（其實B-是由B-tree翻譯過來，所以B-樹和B樹是一個概念），它就是一種平衡多路查詢樹。下圖就是一個典型的B樹：
這裡寫圖片描述

從上圖中我們可以大致看到B樹的一些特點，為了更好的描述B樹，我們定義記錄為一個二元組[key, data]，key為記錄的鍵值，data表示其它資料（上圖中只有key，沒有畫出data資料）。下面是對B樹的一個詳細定義：

1. 有一個根節點，根節點只有一個記錄和兩個孩子或者根節點為空；
2. 每個節點記錄中的key和指標相互間隔，指標指向孩子節點；
3. d是表示樹的寬度，除葉子節點之外，其它每個節點有[d/2,d-1]條記錄，並且些記錄中的key都是從左到右按大小排列的，有[d/2+1,d]個孩子；
4. 在一個節點中，第n個子樹中的所有key，小於這個節點中第n個key，大於第n-1個key，比如上圖中B節點的第2個子節點E中的所有key都小於B中的第2個key 9，大於第1個key 3;
5. 所有的葉子節點必須在同一層次，也就是它們具有相同的深度；

由於B-Tree的特性，在B-Tree中按key檢索資料的演算法非常直觀：首先從根節點進行二分查詢，如果找到則返回對應節點的data，否則對相應區間的指標指向的節點遞迴進行查詢，直到找到節點或找到null指標，前者查詢成功，後者查詢失敗。B-Tree上查詢演算法的虛擬碼如下：

BTree_Search(node, key) {
     if(node == null) return null;
     foreach(node.key){
          if(node.key[i] == key) return node.data[i];
          if(node.key[i] > key) return BTree_Search(point[i]->node);
      }
     return BTree_Search(point[i+1]->node);
  }
data = BTree_Search(root, my_key);

關於B-Tree有一系列有趣的性質，例如一個度為d的B-Tree，設其索引N個key，則其樹高h的上限為logd((N+1)/2)，檢索一個key，其查詢節點個數的漸進複雜度為O(logdN)。從這點可以看出，B-Tree是一個非常有效率的索引資料結構。

另外，由於插入刪除新的資料記錄會破壞B-Tree的性質，因此在插入刪除時，需要對樹進行一個分裂、合併、轉移等操作以保持B-Tree性質，本文不打算完整討論B-Tree這些內容，因為已經有許多資料詳細說明了B-Tree的數學性質及插入刪除演算法，有興趣的朋友可以查閱其它文獻進行詳細研究。

2.3.2 B+Tree

其實B-Tree有許多變種，其中最常見的是B+Tree，比如MySQL就普遍使用B+Tree實現其索引結構。B-Tree相比，B+Tree有以下不同點：

每個節點的指標上限為2d而不是2d+1；
內節點不儲存data，只儲存key；
葉子節點不儲存指標；

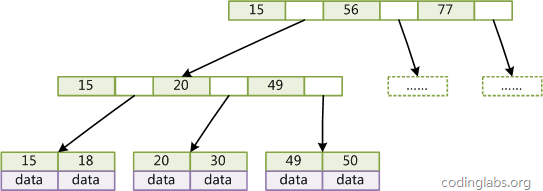
下面是一個簡單的B+Tree示意。
這裡寫圖片描述

由於並不是所有節點都具有相同的域，因此B+Tree中葉節點和內節點一般大小不同。這點與B-Tree不同，雖然B-Tree中不同節點存放的key和指標可能數量不一致，但是每個節點的域和上限是一致的，所以在實現中B-Tree往往對每個節點申請同等大小的空間。一般來說，B+Tree比B-Tree更適合實現外儲存索引結構，具體原因與外儲存器原理及計算機存取原理有關，將在下面討論。

2.3.3 帶有順序訪問指標的B+Tree

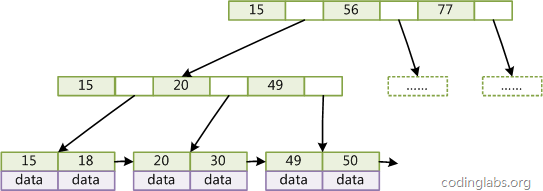
一般在資料庫系統或檔案系統中使用的B+Tree結構都在經典B+Tree的基礎上進行了優化，增加了順序訪問指標。
這裡寫圖片描述

如圖所示，在B+Tree的每個葉子節點增加一個指向相鄰葉子節點的指標，就形成了帶有順序訪問指標的B+Tree。做這個優化的目的是為了提高區間訪問的效能，例如圖4中如果要查詢key為從18到49的所有資料記錄，當找到18後，只需順著節點和指標順序遍歷就可以一次性訪問到所有資料節點，極大提到了區間查詢效率。

這一節對B-Tree和B+Tree進行了一個簡單的介紹，下一節結合儲存器存取原理介紹為什麼目前B+Tree是資料庫系統實現索引的首選資料結構。

三、索引資料結構設相關的計算機原理

上文說過，二叉樹、紅黑樹等資料結構也可以用來實現索引，但是檔案系統及資料庫系統普遍採用B-/+Tree作為索引結構，這一節將結合計算機組成原理相關知識討論B-/+Tree作為索引的理論基礎。

3.1 兩種型別的儲存

在計算機系統中一般包含兩種型別的儲存，計算機主存（RAM）和外部儲存器（如硬碟、CD、SSD等）。在設計索引演算法和儲存結構時，我們必須要考慮到這兩種型別的儲存特點。主存的讀取速度快，相對於主存，外部磁碟的資料讀取速率要比主從慢好幾個數量級，具體它們之間的差別後面會詳細介紹。上面講的所有查詢演算法都是假設資料儲存在計算機主存中的，計算機主存一般比較小，實際資料庫中資料都是儲存到外部儲存器的。

一般來說，索引本身也很大，不可能全部儲存在記憶體中，因此索引往往以索引檔案的形式儲存的磁碟上。這樣的話，索引查詢過程中就要產生磁碟I/O消耗，相對於記憶體存取，I/O存取的消耗要高几個數量級，所以評價一個數據結構作為索引的優劣最重要的指標就是在查詢過程中磁碟I/O操作次數的漸進複雜度。換句話說，索引的結構組織要儘量減少查詢過程中磁碟I/O的存取次數。下面詳細介紹記憶體和磁碟存取原理，然後再結合這些原理分析B-/+Tree作為索引的效率。

3.2 主存存取原理

目前計算機使用的主存基本都是隨機讀寫儲存器（RAM），現代RAM的結構和存取原理比較複雜，這裡本文拋卻具體差別，抽象出一個十分簡單的存取模型來說明RAM的工作原理。
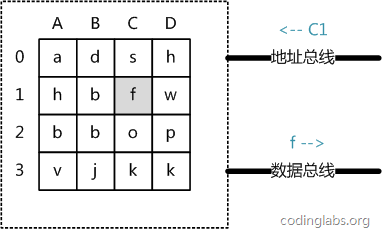
這裡寫圖片描述

從抽象角度看，主存是一系列的儲存單元組成的矩陣，每個儲存單元儲存固定大小的資料。每個儲存單元有唯一的地址，現代主存的編址規則比較複雜，這裡將其簡化成一個二維地址：通過一個行地址和一個列地址可以唯一定位到一個儲存單元。上圖展示了一個4 x 4的主存模型。

主存的存取過程如下：

當系統需要讀取主存時，則將地址訊號放到地址總線上傳給主存，主存讀到地址訊號後，解析訊號並定位到指定儲存單元，然後將此儲存單元資料放到資料匯流排上，供其它部件讀取。寫主存的過程類似，系統將要寫入單元地址和資料分別放在地址匯流排和資料匯流排上，主存讀取兩個匯流排的內容，做相應的寫操作。

這裡可以看出，主存存取的時間僅與存取次數呈線性關係，因為不存在機械操作，兩次存取的資料的“距離”不會對時間有任何影響，例如，先取A0再取A1和先取A0再取D3的時間消耗是一樣的。

3.3 磁碟存取原理

上文說過，索引一般以檔案形式儲存在磁碟上，索引檢索需要磁碟I/O操作。與主存不同，磁碟I/O存在機械運動耗費，因此磁碟I/O的時間消耗是巨大的。

磁碟讀取資料靠的是機械運動，當需要從磁碟讀取資料時，系統會將資料邏輯地址傳給磁碟，磁碟的控制電路按照定址邏輯將邏輯地址翻譯成實體地址，即確定要讀的資料在哪個磁軌，哪個扇區。為了讀取這個扇區的資料，需要將磁頭放到這個扇區上方，為了實現這一點，磁頭需要移動對準相應磁軌，這個過程叫做尋道，所耗費時間叫做尋道時間，然後磁碟旋轉將目標扇區旋轉到磁頭下，這個過程耗費的時間叫做旋轉時間，最後便是對讀取資料的傳輸。所以每次讀取資料花費的時間可以分為尋道時間、旋轉延遲、傳輸時間三個部分。其中：

尋道時間是磁臂移動到指定磁軌所需要的時間，主流磁碟一般在5ms以下。
旋轉延遲就是我們經常聽說的磁碟轉速，比如一個磁碟7200轉，表示每分鐘能轉7200次，也就是說1秒鐘能轉120次，旋轉延遲就是1/120/2 = 4.17ms。
傳輸時間指的是從磁碟讀出或將資料寫入磁碟的時間，一般在零點幾毫秒，相對於前兩個時間可以忽略不計。

那麼訪問一次磁碟的時間，即一次磁碟IO的時間約等於5+4.17 = 9ms左右，聽起來還挺不錯的，但要知道一臺500 -MIPS的機器每秒可以執行5億條指令，因為指令依靠的是電的性質，換句話說執行一次IO的時間可以執行40萬條指令，資料庫動輒十萬百萬乃至千萬級資料，每次9毫秒的時間，顯然是個災難。

3.4 區域性性原理與磁碟預讀

由於儲存介質的特性，磁碟本身存取就比主存慢很多，再加上機械運動耗費，磁碟的存取速度往往是主存的幾百分分之一，因此為了提高效率，要儘量減少磁碟I/O。為了達到這個目的，磁碟往往不是嚴格按需讀取，而是每次都會預讀，即使只需要一個位元組，磁碟也會從這個位置開始，順序向後讀取一定長度的資料放入記憶體。這樣做的理論依據是電腦科學中著名的區域性性原理：當一個數據被用到時，其附近的資料也通常會馬上被使用。程式執行期間所需要的資料通常比較集中。

由於磁碟順序讀取的效率很高（不需要尋道時間，只需很少的旋轉時間），因此對於具有區域性性的程式來說，預讀可以提高I/O效率。預讀的長度一般為頁（page）的整倍數。頁是計算機管理儲存器的邏輯塊，硬體及作業系統往往將主存和磁碟儲存區分割為連續的大小相等的塊，每個儲存塊稱為一頁（在許多作業系統中，頁得大小通常為4k），主存和磁碟以頁為單位交換資料。當程式要讀取的資料不在主存中時，會觸發一個缺頁異常，此時系統會向磁碟發出讀盤訊號，磁碟會找到資料的起始位置並向後連續讀取一頁或幾頁載入記憶體中，然後異常返回，程式繼續執行。

四、資料庫索引所採用的資料結構B-/+Tree及其效能分析

到這裡終於可以分析為何資料庫索引採用B-/+Tree儲存結構了。上文說過資料庫索引是儲存到磁碟的而我們又一般以使用磁碟I/O次數來評價索引結構的優劣。先從B-Tree分析，根據B-Tree的定義，可知檢索一次最多需要訪問h-1個節點（根節點常駐記憶體）。資料庫系統的設計者巧妙利用了磁碟預讀原理，將一個節點的大小設為等於一個頁，這樣每個節點只需要一次I/O就可以完全載入。為了達到這個目的，在實際實現B-Tree還需要使用如下技巧：每次新建節點時，直接申請一個頁的空間，這樣就保證一個節點物理上也儲存在一個頁裡，加之計算機儲存分配都是按頁對齊的，就實現了一個node只需一次I/O。

B-Tree中一次檢索最多需要h-1次I/O（根節點常駐記憶體），漸進複雜度為O(h)=O(logdN)。一般實際應用中，出度d是非常大的數字，通常超過100，因此h非常小（通常不超過3）。

綜上所述，如果我們採用B-Tree儲存結構，搜尋時I/O次數一般不會超過3次，所以用B-Tree作為索引結構效率是非常高的。

4.1 B+樹效能分析

從上面介紹我們知道，B樹的搜尋複雜度為O(h)=O(logdN)，所以樹的出度d越大，深度h就越小，I/O的次數就越少。B+Tree恰恰可以增加出度d的寬度，因為每個節點大小為一個頁大小，所以出度的上限取決於節點內key和data的大小：

dmax=floor(pagesize/(keysize+datasize+pointsize))//floor表示向下取整

由於B+Tree內節點去掉了data域，因此可以擁有更大的出度，從而擁有更好的效能。

4.2 B+樹查詢過程

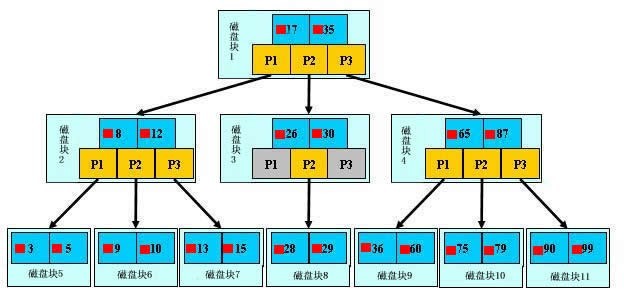
這裡寫圖片描述
B-樹和B+樹查詢過程基本一致。如上圖所示，如果要查詢資料項29，那麼首先會把磁碟塊1由磁碟載入到記憶體，此時發生一次IO，在記憶體中用二分查詢確定29在17和35之間，鎖定磁碟塊1的P2指標，記憶體時間因為非常短（相比磁碟的IO）可以忽略不計，通過磁碟塊1的P2指標的磁碟地址把磁碟塊3由磁碟載入到記憶體，發生第二次IO，29在26和30之間，鎖定磁碟塊3的P2指標，通過指標載入磁碟塊8到記憶體，發生第三次IO，同時記憶體中做二分查詢找到29，結束查詢，總計三次IO。真實的情況是，3層的b+樹可以表示上百萬的資料，如果上百萬的資料查詢只需要三次IO，效能提高將是巨大的，如果沒有索引，每個資料項都要發生一次IO，那麼總共需要百萬次的IO，顯然成本非常非常高。

這一章從理論角度討論了與索引相關的資料結構與演算法問題，下一章將討論B+Tree是如何具體實現為MySQL中索引，同時將結合MyISAM和InnDB儲存引擎介紹非聚集索引和聚集索引兩種不同的索引實現形式。

五、MySQL索引實現

在MySQL中，索引屬於儲存引擎級別的概念，不同儲存引擎對索引的實現方式是不同的，本文主要討論MyISAM和InnoDB兩個儲存引擎的索引實現方式。

5.1 MyISAM索引實現

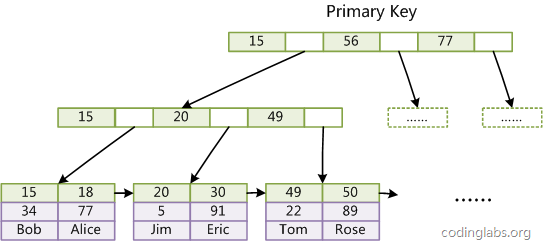
MyISAM引擎使用B+Tree作為索引結構，葉節點的data域存放的是資料記錄的地址。下圖是MyISAM索引的原理圖：
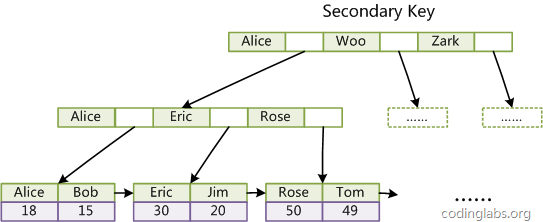
這裡寫圖片描述

這裡設表一共有三列，假設我們以Col1為主鍵，則上圖是一個MyISAM表的主索引（Primary key）示意。可以看出MyISAM的索引檔案僅僅儲存資料記錄的地址。在MyISAM中，主索引和輔助索引（Secondary key）在結構上沒有任何區別，只是主索引要求key是唯一的，而輔助索引的key可以重複。如果我們在Col2上建立一個輔助索引，則此索引的結構如下圖所示：
這裡寫圖片描述

同樣也是一顆B+Tree，data域儲存資料記錄的地址。因此，MyISAM中索引檢索的演算法為首先按照B+Tree搜尋演算法搜尋索引，如果指定的Key存在，則取出其data域的值，然後以data域的值為地址，讀取相應資料記錄。
MyISAM的索引方式也叫做“非聚集”的，之所以這麼稱呼是為了與InnoDB的聚集索引區分。

5.2 InnoDB索引實現

雖然InnoDB也使用B+Tree作為索引結構，但具體實現方式卻與MyISAM截然不同。

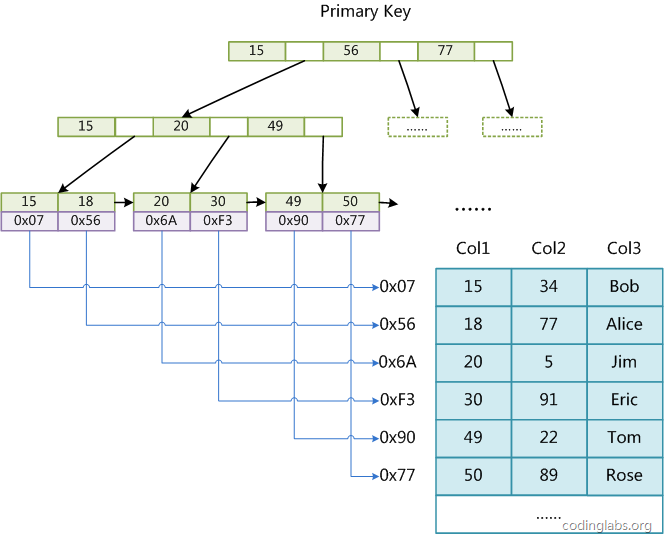
第一個重大區別是InnoDB的資料檔案本身就是索引檔案。從上文知道，MyISAM索引檔案和資料檔案是分離的，索引檔案僅儲存資料記錄的地址。而在InnoDB中，表資料檔案本身就是按B+Tree組織的一個索引結構，這棵樹的葉節點data域儲存了完整的資料記錄。這個索引的key是資料表的主鍵，因此InnoDB表資料檔案本身就是主索引。
這裡寫圖片描述

上圖是InnoDB主索引（同時也是資料檔案）的示意圖，可以看到葉節點包含了完整的資料記錄。這種索引叫做聚集索引。因為InnoDB的資料檔案本身要按主鍵聚集，所以InnoDB要求表必須有主鍵（MyISAM可以沒有），如果沒有顯式指定，則MySQL系統會自動選擇一個可以唯一標識資料記錄的列作為主鍵，如果不存在這種列，則MySQL自動為InnoDB表生成一個隱含欄位作為主鍵，這個欄位長度為6個位元組，型別為長整形。

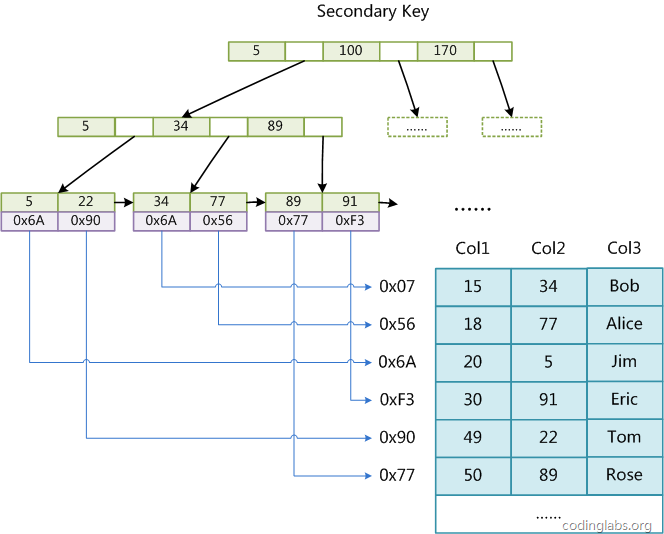
第二個與MyISAM索引的不同是InnoDB的輔助索引data域儲存相應記錄主鍵的值而不是地址。換句話說，InnoDB的所有輔助索引都引用主鍵作為data域。例如，下圖為定義在Col3上的一個輔助索引：
這裡寫圖片描述

這裡以英文字元的ASCII碼作為比較準則。聚集索引這種實現方式使得按主鍵的搜尋十分高效，但是輔助索引搜尋需要檢索兩遍索引：首先檢索輔助索引獲得主鍵，然後用主鍵到主索引中檢索獲得記錄。

瞭解不同儲存引擎的索引實現方式對於正確使用和優化索引都非常有幫助，例如知道了InnoDB的索引實現後，就很容易明白為什麼不建議使用過長的欄位作為主鍵，因為所有輔助索引都引用主索引，過長的主索引會令輔助索引變得過大。再例如，用非單調的欄位作為主鍵在InnoDB中不是個好主意，因為InnoDB資料檔案本身是一顆B+Tree，非單調的主鍵會造成在插入新記錄時資料檔案為了維持B+Tree的特性而頻繁的分裂調整，十分低效，而使用自增欄位作為主鍵則是一個很好的選擇。

下一章將具體討論這些與索引有關的優化策略。

六、索引使用策略及優化

MySQL的優化主要分為結構優化（Scheme optimization）和查詢優化（Query optimization）。本章討論的高效能索引策略主要屬於結構優化範疇。本章的內容完全基於上文的理論基礎，實際上一旦理解了索引背後的機制，那麼選擇高效能的策略就變成了純粹的推理，並且可以理解這些策略背後的邏輯。

6.1 聯合索引及最左字首原理

聯合索引（複合索引）

首先介紹一下聯合索引。聯合索引其實很簡單，相對於一般索引只有一個欄位，聯合索引可以為多個欄位建立一個索引。它的原理也很簡單，比如，我們在（a,b,c）欄位上建立一個聯合索引，則索引記錄會首先按照A欄位排序，然後再按照B欄位排序然後再是C欄位，因此，聯合索引的特點就是：

第一個欄位一定是有序的
當第一個欄位值相等的時候，第二個欄位又是有序的，比如下表中當A=2時所有B的值是有序排列的，依次類推，當同一個B值得所有C欄位是有序排列的

| A | B | C |
| 1 | 2 | 3 |
| 1 | 4 | 2 |
| 1 | 1 | 4 |
| 2 | 3 | 5 |
| 2 | 4 | 4 |
| 2 | 4 | 6 |
| 2 | 5 | 5 |

其實聯合索引的查詢就跟查字典是一樣的，先根據第一個字母查，然後再根據第二個字母查，或者只根據第一個字母查，但是不能跳過第一個字母從第二個字母開始查。這就是所謂的最左字首原理。

最左字首原理

我們再來詳細介紹一下聯合索引的查詢。還是上面例子，我們在（a,b,c）欄位上建了一個聯合索引，所以這個索引是先按a 再按b 再按c進行排列的，所以：

以下的查詢方式都可以用到索引

select * from table where a=1；
select * from table where a=1 and b=2；
select * from table where a=1 and b=2 and c=3；

上面三個查詢按照 （a ）, （a，b ）,（a，b，c ）的順序都可以利用到索引，這就是最左字首匹配。

如果查詢語句是：

select * from table where a=1 and c=3； 那麼只會用到索引a。