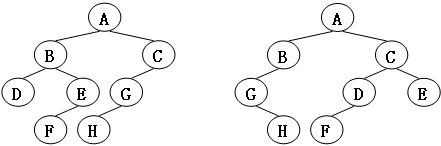
給定兩棵樹T1和T2。如果T1可以通過若干次左右孩子互換就變成T2，則我們稱兩棵樹是“同構”的。例如圖1給出的兩棵樹就是同構的，因為我們把其中一棵樹的結點A、B、G的左右孩子互換後，就得到另外一棵樹。而圖2就不是同構的。

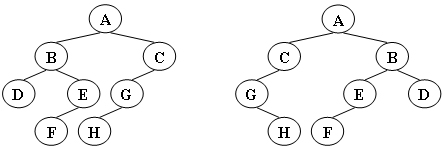
圖1

圖2

現給定兩棵樹，請你判斷它們是否是同構的。

輸入格式:

輸入給出2棵二叉樹樹的資訊。對於每棵樹，首先在一行中給出一個非負整數$N$ (≤)，即該樹的結點數（此時假設結點從0到$N-1$編號）；隨後$N$行，第$i$行對應編號第$i$個結點，給出該結點中儲存的1個英文大寫字母、其左孩子結點的編號、右孩子結點的編號。如果孩子結點為空，則在相應位置上給出“-”。給出的資料間用一個空格分隔。注意：題目保證每個結點中儲存的字母是不同的。

輸出格式:

如果兩棵樹是同構的，輸出“Yes”，否則輸出“No”。

輸入樣例1（對應圖1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

輸出樣例1:

Yes

輸入樣例2（對應圖2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

輸出樣例2:

No

思路：比較根節點，如果相同，找出其相同的孩子，進行遞迴。

#include<iostream>

#include<string.h>
using namespace std;
typedef struct Tree{
char point;
int lchild;
int rchild;
}Tree;
Tree t1[12],t2[12];//兩棵樹


int CreateTree(Tree t[],int &n){
int check[11];
char l,r;
memset(check,0,sizeof(check));
cin>>n;
for(int i = 0;i<n;i++){
cin>>t[i].point>>l>>r;
if(l!='-'){
t[i].lchild = l-'0';
check[t[i].lchild] = 1;
}
else
t[i].lchild = -1;
if(r!='-'){
t[i].rchild = r-'0';
check[t[i].rchild] = 1;
}
else
t[i].rchild = -1;
}
for(int j = 0;j<n;j++)
if(check[j]==0)
return j;
return -1;
}
bool isTongGou(int rt1,int rt2){
if(rt1==-1&&rt2==-1)//同為空樹返回true
return true;
if(t1[rt1].point==t2[rt2].point)
//如果是同構的話，tree1的左孩子等於tree2的左孩子或者右孩子。其實一直都是在比較根節點，遞迴即可。
return t1[t1[rt1].lchild].point==t2[t2[rt1].lchild].point?isTongGou(t1[rt1].lchild,t2[rt2].lchild):isTongGou(t1[rt1].lchild,t2[rt2].rchild);
return false;
}
int main(){
int root1,root2;
int n,m;//每棵樹的節點數（因為最後有個節點數不同的測試點就是過不了，在函式中沒能解決，只好出此下策）
root1 = CreateTree(t1,n);//建樹並且返回根節點
root2 = CreateTree(t2,m);
if(isTongGou(root1,root2)&&n==m){
cout<<"Yes"<<endl;
}
else
cout<<"No"<<endl;
return 0;
}