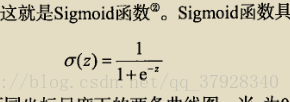邏輯迴歸例項:從疝氣病預測病馬的死亡率
先了解大致模型建立的流程,接下來我會弄一些演算法的原理及梯度上升的對比:
資料有三部分:
梯度演算法公式:
附完整版程式碼:
from numpy import *
import numpy as np
def loadDataSet():
dataMat = [];
labelMat = []
fr = open('D:\\machinelearn_data\\testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
print(int(lineArr[2]))
# strip() 方法用於移除字串頭尾指定的字元(預設為空格)
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
# 第一列是1,另外加的,即形如[1,x1,x2]
labelMat.append(int(lineArr[2]))
#print(labelMat)
return dataMat, labelMat # 此時是陣列
def sigmoid(inX):
return 1.0 / (1 + exp(-inX)) # 返回一個0-1的100*1的陣列
# 梯度上升
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) # convert to NumPy matrix # 轉換成numpy矩陣(matrix),dataMatrix:100*3
labelMat = mat(classLabels).transpose() # convert to NumPy matrix # transpose轉置為100*1
m, n = shape(dataMatrix) # 得到行和列數,0代表行數,1代表列數
alpha = 0.001 # 步長
maxCycles = 500 # 最大迭代次數
weights = ones((n, 1)) # 3*1的矩陣,其權係數個數由給定訓練集的維度值和類別值決定
for k in range(maxCycles): # heavy on matrix operations
h = sigmoid(dataMatrix * weights) # matrix mult # 利用對數機率迴歸,z = w0 +w1*X1+w2*X2,w0相當於b
error = (labelMat - h) # vector subtraction
weights = weights + alpha * dataMatrix.transpose() * error # matrix mult # 一種極大似然估計的推到過程,但每次的權係數更新都要遍歷整個資料集
return weights
# 畫出資料集和Logistic分類直線的函式
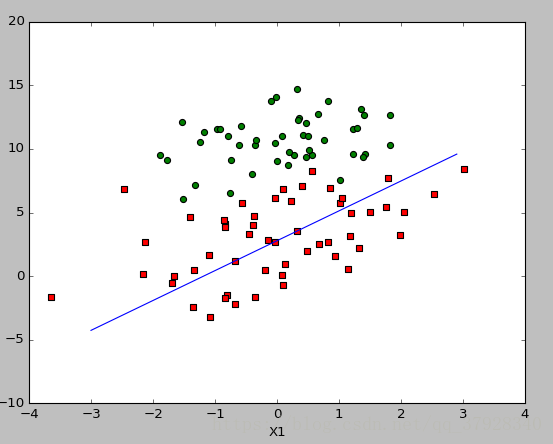
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat, labelMat = loadDataSet() # 載入資料集,訓練資料和標籤
dataArr = array(dataMat) # 進行資料處理,必須轉換為numpy中的array
n = shape(dataArr)[0] # 樣本個數
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1]) # 一類
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1]) # 另一類
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') # 散點圖
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
# print(type(x))
y = (-weights[0] - weights[1] * x) / weights[2] # 換算後的簡化形式
y1 = y.T # 轉置換型別 或者其他api都可以試試
# print(type(y))
# m,b = np.polyfit(x,y)
ax.plot(x, y1)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
# 梯度上升演算法
"""
設定迴圈迭代次數,權重係數的每次更新是榮國計算所有樣本得出來的,當訓練集過於龐大不利於計算
"""
def stocGradAscent0(dataMatrix, classLabels):
m, n = shape(dataMatrix)
alpha = 0.01 # x學習率
weights = ones(n) # initialize to all ones
for i in range(m):
h = sigmoid(sum(dataMatrix[i] * weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
# 隨機梯度上升
"""
對梯度上升演算法進行改進,權重係數的每次更新通過訓練集的每個記錄計算得到
可以在新樣本到來時分類器進行增量式更新,因為隨機梯度演算法是個更新權重的演算法
但是演算法容易受到噪聲點的影響。在大的波動停止後,還有小週期的波動
"""
"""
前者的h,error 都是數值,前者沒有矩陣轉換過程,後者都是向量,資料型別則變為numpy
"""
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
m, n = shape(dataMatrix)
weights = ones(n) # initialize to all ones
for j in range(numIter):
dataIndex = range(m)
for i in range(m):
alpha = 4 / (1.0 + j + i) + 0.0001 # apha decreases with iteration, does not
randIndex = int(random.uniform(0, len(dataIndex))) # go to 0 because of the constant
h = sigmoid(sum(dataMatrix[randIndex] * weights))
error = classLabels[randIndex] - h
# 學習率:變化。隨著迭代次數的增多,逐漸變下。
# 權重係數更新:設定迭代次數,每次更新選擇的樣例是隨機的(不是依次選的)。
weights = weights + alpha * error * dataMatrix[randIndex] # 分類函式
# 為什麼刪除變數?
#print(list(dataIndex)[randIndex])
del (list(dataIndex)[randIndex])
return weights
# 分類演算法
def classifyVector(inX, weights):
prob = sigmoid(sum(inX * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
# 測試演算法
"""
為了量化迴歸效果,使用錯誤率作為觀察指標。根據錯誤率決定是否回退到訓練階段,通過改變迭代次數和步驟等引數來得到更好的迴歸係數。
"""
def colicTest():
frTrain = open('D:\\machinelearn_data\\horseColicTraining.txt', encoding='utf8');
frTest = open('D:\\machinelearn_data\\horseColicTest.txt', encoding='utf8')
trainingSet = []
trainingLabels = []
# print(frTest)
# print(frTrain)
for line in frTrain.readlines():
currLine = line.strip().split('\t')
lineArr = []
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000)
errorCount = 0;
numTestVec = 0.0
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr = []
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(array(lineArr), trainWeights)) != int(currLine[21]):
errorCount += 1
errorRate = (float(errorCount) / numTestVec)
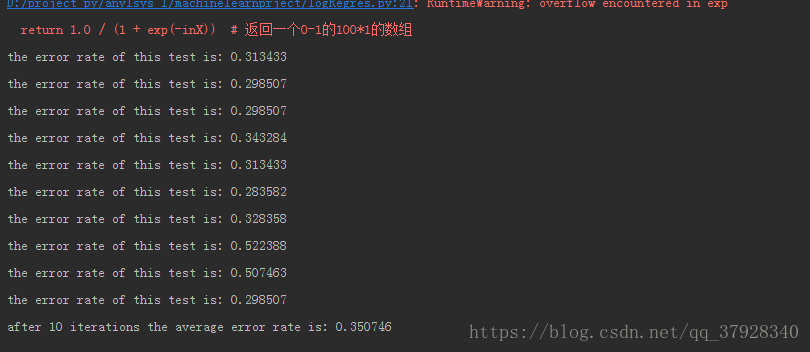
print("the error rate of this test is: %f" % errorRate)
return errorRate
# 通過多次測試,取平均,作為該分類器錯誤率
"""
優點:計算代價不高,易於理解和實現;
缺點:容易欠擬合,分類進度可能不高;
使用資料型別:數值型和標稱型資料。
"""
def multiTest():
numTests = 10
errorSum = 0.0
for k in range(numTests):
errorSum += colicTest()
print("after %d iterations the average error rate is: %f" % (numTests, errorSum / float(numTests)))
if __name__ == '__main__':
# 入口函式:模型引數y=wx
dataArr, labelMat = loadDataSet()
#weights = gradAscent(dataArr, labelMat) # dataArr:100*3,labelMat是一個列表
weights = stocGradAscent1(array(dataArr),labelMat ,150)
plotBestFit(weights)
multiTest()
梯度優化示意圖:
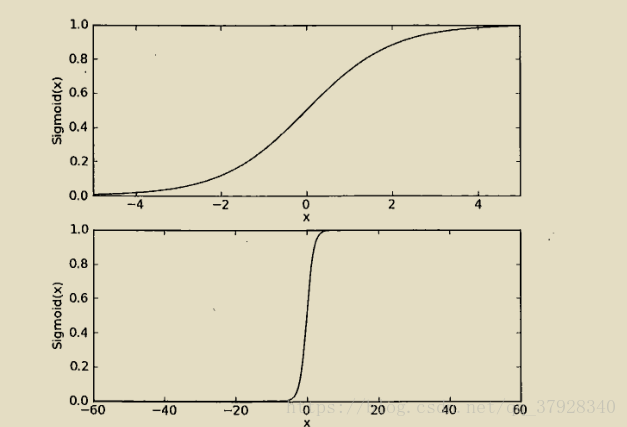
主要是對sigmoid函式的理解,如圖,知道變數的變化範圍,最優解,及跳躍函式的理解,就基本瞭解邏輯函式分類的原理了
不當之處,多多理解