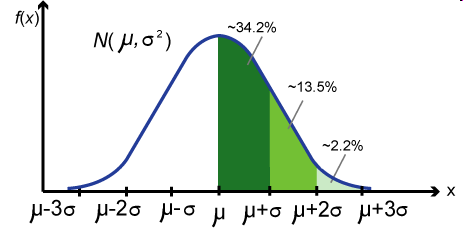
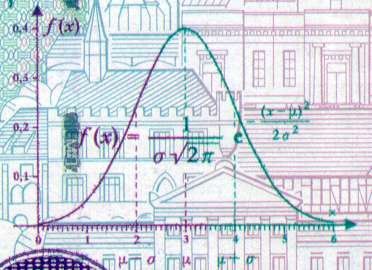正態分佈的前世今生(壹)
更加的簡潔漂亮,兩個最重要的數學常量
正態分佈又通常被稱為高斯分佈,在科學領域,冠名權那是一個很高的榮譽。2002年以前去過德國的兄弟們還會發現,德國1991年至2001年間發行的的一款10馬克的紙幣上印著高斯(Carl Friedrich Gauss, 1777-1855)的頭像和正態密度曲線,而1977年東德發行的20馬克的可流通紀念鋼鏰上,也印著正態分佈曲線和高斯的名字。正態分佈被冠名高斯分佈,我們也容易認為是高斯發現了正態分佈,其實不然,不過高斯對於正態分佈的歷史地位的確立是起到了決定性的作用。
正態曲線雖然看上去很美,卻不是一拍腦袋就能想到的。我們在本科學習數理統計的時候,課本一上來介紹正態分佈就給出分佈密度函式,卻從來不說明這個密度函式是通過什麼原理推匯出來的。所以我一直搞不明白數學家當年是怎麼找到這個概率分佈曲線的,又是怎麼發現隨機誤差服從這個奇妙的分佈的。我們在實踐中大量的使用正態分佈,卻對這個分佈的來龍去脈知之甚少,正態分佈真是讓人感覺既熟悉又陌生。直到我讀研究生的時候,我的導師給我介紹了陳希儒院士的《數理統計學簡史》這本書,看了之後才瞭解了正態分佈曲線從發現到被人們重視進而廣泛應用,也是經過了幾百年的歷史。
正態分佈的這段歷史是很精彩的,我們通過講一系列的故事來揭開她的神祕面紗。
2. 邂逅,正態曲線的首次發現
第一個故事和概率論的發展密切相關,主角是棣莫弗(Abraham de Moivre, 1667-1754) 和拉普拉斯 (Pierre-Simon Laplace 1749-1827)。拉普拉斯是個大科學家,被稱為法國的牛頓;棣莫弗名氣可能不算很大,不過大家應該都應該很熟悉這個名字,因為我們在高中數學學複數的時候都學過棣莫弗公式
古典概率論發源於賭博,惠更斯(Christiaan Huygens, 1629-1695)、帕斯卡(Blaise Pascal, 1623-1662)、費馬(Pierre de Fermat, 1601-1665)、雅可比·貝努利(Jacob Bernoulli, 1654-1705)都是古典概率的奠基人,他們那會研究的概率問題大都來自賭桌上,最早的概率論問題是賭徒梅累在1654年向帕斯卡提出的如何分賭金的問題。統計學中的總體均值之所以被稱為期望 (Expectation), 就是源自惠更斯、帕斯卡這些人研究平均情況下一個賭徒在賭桌上可以期望自己贏得多少錢。
有一天一個哥們,也許是個賭徒,向棣莫弗提了一個和賭博相關的問題:A、B 兩人在賭場裡賭博,A、B各自的獲勝概率是
問題並不複雜, 本質上是一個二項分佈,若
其中
與此相關聯的另一個問題,是遵從二項分佈的隨機變數
對於
事實上斯特林公式的雛形是棣莫弗最先得到的,但斯特林改進了這個公式,改進的結果為棣莫弗所用。1733 年,棣莫弗很快利用斯特林公式進行計算並取得了重要的進展。考慮
以下把
於是有
使用上式的結果,並在二項概率累加求和的過程中近似的使用定積分代替求和,很容易就能得到
看,正態分佈的密度函式的形式在積分公式中出現了!這也就是我們在數理統計課本上學到的一個重要結論:二項分佈的極限分佈是正態分佈。
以上只是討論了
[棣莫弗-拉普拉斯中心極限定理]設隨機變數
相關推薦
正態分佈的前世今生(壹)
也非常具有數學的美感。其標準化後的概率密度函式 更加的簡潔漂亮,兩個最重要的數學常量 π、e 都出現在這公式之中。在我個人的審美之中,它也屬於 top-N 的最美麗的數學公式之一,如果有人問我數理統計領域哪個公式最能讓人感覺到上帝的存在,那我一定投正態分佈的票。因為這個分佈戴著神祕的面紗
正態分佈的前世今生(貳)
6. 開疆拓土,正態分佈的進一步發展 19世紀初,隨著拉普拉斯中心極限定理的建立與高斯正態誤差理論的問世,正態分佈開始嶄露頭角,逐步在近代概率論和數理統計學中大放異彩。在概率論中,由於拉普拉斯的推動,中心極限定理髮展成為現代概率論的一塊基石。而在數理統計學中,在高斯的大力提倡之下,正態分佈開始逐
Excel圖表—標準正態分佈概率分佈圖(概率密度函式圖及累積概率分佈圖)的繪製
看似很簡單的一張Excel圖表,實際上也花了10多分鐘。這對於已經習慣了Spotfire這種資料視覺化軟體的我而言是不能接受的。 不過,功夫不負有心人,總算是畫出了教科書上的效果。 以下是一點小創新,如果提高資料粒度(資料粒度能夠滿足業務要求),有些問題的答案將一目瞭然
TWaver可視化編輯器的前世今生(四)電力 雲計算 數據中心
變電站 fontsize 復雜 部署 ood 配置信息 來看 tar 右鍵 插播一則廣告(長期有效) TWaver需要在武漢招JavaScript工程師若幹 要求:對前端技術(JavasScript、HTML、CSS),對可視化技術(Canvas、WebGL)有濃厚的興
SQLMap的前世今生(Part1)
節點 如何 所在 having image character mysql 最大 格式 http://www.freebuf.com/sectool/77948.html 一、前言 談到SQL註入,第一時間就會想到神器SQLMAP,SQLMap是一款用來檢測與利用的SQ
java中字元與字串的前世今生(上)
Unicode碼錶 在介紹char型別之前我們先介紹一下Unicode.以下是百度百科給出的解釋: Unicode(統一碼、萬國碼、單一碼)是電腦科學領域裡的一項業界標準,包括字符集、編碼方案等。Unicode 是為了解決傳統的字元編碼方案的侷限而產生的,它為
DevOps的前世今生(2)Dev和Ops矛盾緣何而來 ?
本文經授權轉載簡書作者:顧宇 原文:http://www.jianshu.com/p/c6573e63c752 前言 在#DevOps的前世今生# 1. DevOps編年史一文中,通過追溯 DevOps 活動產生的歷史起源,我們發現了 DevOps 是敏捷思想從軟體開發端(Dev)到系統維護端(O
DevOps的前世今生(3) DevOps的目標和手段
本文經授權轉載簡書作者:顧宇 原文:http://www.jianshu.com/p/c6573e63c752 前言 在#DevOps的前世今生# 2. Dev和Ops矛盾緣何而來 ?一文中,通過Dev和Ops的歷史發展總結出了Dev和Ops矛盾的歷史淵源,以及 Dev 和 Ops 的核心矛盾:
DevOps的前世今生(1)DevOps編年史
本文經授權轉載簡書作者:顧宇 原文:http://www.jianshu.com/p/c6573e63c752 Time 1:2007 年 比利時,一個沮喪的獨立IT諮詢師 DevOps 的歷史要從一個比利時的獨立IT諮詢師說起。這位諮詢師的名字叫做Patrick Debois,他喜歡從各個角
【深度學習】Inception的前世今生(一)--GoogLeNet
在2014年ILSVRC比賽上,GoogleNet 用了僅僅是AlexNet的12%的引數量,卻拿到了分類top-5的第一名。在之前的深度學習網路的設計中,會存在兩個重要缺陷: 1) 更深更寬的網路模型會產生巨量引數 2) 網路規模的加大會極大的增加計算
【深度學習】Inception的前世今生(三)--Inception V3
論文題目:《Rethinking the Inception Architecture for Computer Vision》 論文連結:https://arxiv.org/abs/1512.00567 自從2014年GoogLeNet在ImageNet上
垃圾回收算法的前世今生(轉)
如果 內存回收 碎片 新生代 大片 全面 堆區 邊界 垃圾回收 1.引用計數法(java未采用) 2.標記-清除算發(jvm老年回收) 3.標記-壓縮算發(jvm老年回收) 4.復制算法(jvm新生代回收) 標記-清除算法 標記-清掃式垃圾回收器是一種直接的
圖像語義分割的前世今生(轉載)良心之作
解釋 運行 明顯 視覺 缺點 事情 img 裏的 deep 1998年以來,人工神經網絡識別技術已經引起了廣泛的關註,並且應用
正態分佈(normal distribution)與偏態分佈(skewed distribution)
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
R語言實戰--隨機產生服從不同分佈函式的資料(正態分佈,泊松分佈等),並將資料寫入資料框儲存到硬碟
隨機產生服從不同分佈的資料 均勻分佈——runif() > x1=round(runif(100,min=80,max=100)) > x1 [1] 93 100 98 98 92 98 98 89 90 98 100 89
20.方差/標準差/數學期望/正態分佈/高斯函式(數學篇)--- OpenCV從零開始到影象(人臉 + 物體)識別系列
本文作者:小嗷 微信公眾號:aoxiaoji 吹比QQ群:736854977 本文你會找到以下問題的答案: 方差 標準差 數學期望 正態分佈 高斯函式 2.1 方差 方差描述隨機變數對於數學期望的偏離程度。(隨機變數可以
C#產生正態分佈、泊松分佈、指數分佈、負指數分佈隨機數(原創)
http://blog.sina.com.cn/s/blog_76c31b8e0100qskf.html 在程式設計過程中,由於資料模擬模擬的需要,我們經常需要產生一些隨機數,在C#中,產生一般隨機數用Random即可,但是,若要產生服從特定分佈的隨機數,就需要一定的演
C++生成隨機數:高斯/正態分佈(gaussian/normal distribution)
常用的成熟的生成高斯分佈隨機數序列的方法由Marsaglia和Bray在1964年提出,C++版本如下: #include <stdlib.h> #include <math.h> double gaussrand() { static double V1, V2, S
正態分佈(Normal distribution)與高斯分佈(Gaussian distribution)
正態分佈(Normal distribution)又名高斯分佈(Gaussian distribution),是一個在數學、物理及工程等領域都非常重要的概率分佈,在統計學的許多方面有著重大的影響力。 若隨機變數X服從一個數學期望為μ、標準方差為σ2的高斯分佈,記為: X
【程式設計師眼中的統計學(7)】正態分佈的運用:正態之美
作者 白寧超 2015年10月15日18:30:07 摘要:程式設計師眼中的統計學系列是作者和團隊共同學習筆記的整理。首先提到統計學,很多人認為是經濟學或者數學的專利,與計算機並沒有交集。誠然在傳統學科中,其在以上學科發揮作用很大。然而隨著科學技術的發展和機器智慧的普及,統計學在機器智慧中的作用越來