資料結構之雙親表示法建樹和操作

阿新 • • 發佈：2019-01-26

樹的雙親表示法假設以一組連續空間儲存樹的結點,同時在每個結點中,附設一個指示器指示其雙親結點到連結串列中的位置。也就是說,每個結點除了知道自己是誰以外,還知道它的雙親在哪裡。

雙親表示法的資料儲存結構如下：

#define MAX_TREE_SIZE 100

typedef struct {
	TElemType data;
	int parent;	//指示雙親位置
}PTNode;

typedef struct {
	PTNode	nodes[MAX_TREE_SIZE];
	int n;	//總節點數
}PTree;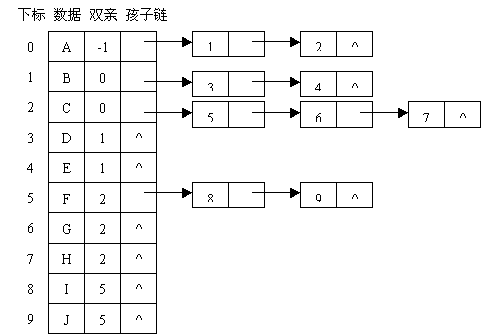

具體的操作如下：

parenttree.h

/*------------------------------------------------------------------------
	*file:ParentTree.c -->head file for ParentTree.c
	*date:10-4-2014
	*author:[email protected]
	*version:1.0
	*description:雙親表示法建樹和操作
-------------------------------------------------------------------------*/

#include "comman.h"

#ifndef _Parent_H

#define MAX_TREE_SIZE 100

typedef struct {
	TElemType data;
	int parent;	//指示雙親位置
}PTNode;

typedef struct {
	PTNode	nodes[MAX_TREE_SIZE];
	int n;	//總節點數
}PTree;




//初始化
Status InitTree(PTree *T);

//建立數
Status CreateTree(PTree *T);

//清空樹
Status ClearTree(PTree *T);

//判空
Status TreeEmpty(PTree T);

//總節點數目
int TreeLength(PTree T);

//求樹的深度
int TreeDepth(PTree T);

//返回樹的根的值
TElemType Root(PTree T);

//返回樹中第i個節點的值
TElemType Value(PTree T,int i);

//修改節點值
Status Assing(PTree *T,TElemType cur_e,TElemType vaule);

//返回父親節點的值
TElemType Parent(PTree T,TElemType cur_e);

//返回左孩子的值
TElemType LeftChild(PTree T,TElemType cur_e);

//返回右兄弟的值
TElemType RightSibling(PTree T,TElemType cur_e);

//返回左兄弟的值
TElemType LeftSibling(PTree T,TElemType cur_e);

//遍歷
Status TreeTraverse(PTree T,Status (*Visit) (TElemType));

//列印元素
Status PrintElem(TElemType elem);

//列印樹
void PrintTree(PTree T);

int GetLine(char *arr,int lim);


#endif

ParentTree.c

/*------------------------------------------------------------------------
	*file:ParentTree.c
	*date:10-4-2014
	*author:[email protected]
	*version:1.0
	*description:雙親表示法建樹和操作
-------------------------------------------------------------------------*/

#include <stdio.h>
#include <string.h>
#include "parenttree.h"
#include "linkqueue.h"

/*
* @descripton:初始化樹
*/
Status InitTree(PTree *T) {
	(*T).n = 0;
	return OK;
}

/*
* @description:建立樹
*/
Status CreateTree(PTree *T) {
	LinkQueue Q;
	QElemType q,qq;
	int i,j,len;

	//莫忘初始化
	i = 0;

	char arr[MAX_TREE_SIZE];	//暫存陣列

	InitQueue(&Q);
	//賦值根節點
	printf("please enter the root of the tree:");
	scanf("%c%*c",&(*T).nodes[0].data);

	if((*T).nodes[0].data != NULL) {
		//根節點沒有父親節點，指向-1
		(*T).nodes[0].parent = -1;
		qq.name = (*T).nodes[0].data;
		qq.num = 0;

		EnQueue(&Q,qq);

		while(i < MAX_TREE_SIZE && !QueueEmpty(Q)) {
			DeQueue(&Q,&qq);
			//輸入每個節點的孩子
			printf("please enter the child of %c:",qq.name);
			
			len = GetLine(arr,MAX_TREE_SIZE);

			if(len < 1)
				break;

			//將每個節點的孩子順序入隊
			for(j = 0; j < len;j++) {
				++i;
				(*T).nodes[i].data = arr[j];
				(*T).nodes[i].parent = qq.num;
				q.num = i;
				q.name = arr[j];
				EnQueue(&Q,q);
			}

		}

		if(i > MAX_TREE_SIZE)
			exit(OVERFLOW);

		(*T).n = i;

		return OK;
	}
	else {
		(*T).n = 0;
		return ERROR;
	}

}

/*
* @description:由於gets不安全,fgets無法滿足要求，故需要實現一個函式獲取不定長的行
*/
int GetLine(char *arr,int lim) {
	char c;
	int i = 0;

	while( (c =getchar()) != '\n' && i < lim)
		arr[i++] = c;

	return i;
}


/*
* @description:清空數(注意這裡的清空僅僅是一種障眼法上的清空)
*/
Status ClearTree(PTree *T)	{
	(*T).n = 0;
	return OK;
}


/*
* @description:判空
*/
Status TreeEmpty(PTree T) {
	return T.n == 0;
}

/*
* @description:返回樹的總節點
*/
int TreeLength(PTree T) {
	return T.n;
}

/*
* @description:求樹的深度
*/
int TreeDepth(PTree T) {
	int k,m,def,max;

	max = 0;
	//這裡的方法在於找到最深的層
	for(k = 0;k < T.n;k++) {
		def = 1;	//初始化本次順尋中def的值
		m = T.nodes[k].parent;

		while(m != -1) {
			m = T.nodes[m].parent;
			def++;
		}
	}

	if(max < def)
		max = def;

	return max;
}

/*
* @description:返回樹的根的值
*/
TElemType Root(PTree T)	{
	if(!TreeEmpty(T))
		return T.nodes[0].data;
	else
		return NULL;
}

/*
* @descripton:返回樹中第i個節點的值
*/
TElemType Value(PTree T,int i) {
	if(i < T.n)
		return T.nodes[i].data;
	else
		return NULL;
}

/*
* @description:cur_e是樹中節點的值,該cur_e為value(保證樹中節點值唯一，否則只能修改第一個)
*/
Status Assign(PTree *T,TElemType cur_e,TElemType value) {
	int i;

	for(i = 0;i < (*T).n ;i++) {
		if((*T).nodes[i].data == cur_e) {
			(*T).nodes[i].data = value;
			return OK;
		}
	}

	return ERROR;
}


/*
* @description:返回父親節點的值
*/
TElemType Parent(PTree T,TElemType cur_e) {
	int i;

	for(i = 0; i < T.n; i++)
		if(T.nodes[i].data == cur_e)
			return T.nodes[T.nodes[i].parent].data;

	return NULL;
}


/*
* @description:根據某個在樹中的值，返回其左孩子的值
		這裡認為最左邊的為左孩子，不存在右孩子的說法
*/
TElemType LeftChild(PTree T,TElemType cur_e) {
	int i,j;

	for(i = 0;i < T.n;i++)
		if(T.nodes[i].data == cur_e)
			break;
	for(j = i+1;j < T.n ;j++)
		if(T.nodes[j].parent == i)
			return T.nodes[j].data;
	
	return NULL;
}

/*
* @description:返回右兄弟的值(這裡的右兄弟是指下一個與它有共同parent的節點)
*/
TElemType RightSibling(PTree T,TElemType cur_e) {
	int i;

	for(i = 0;i < T.n; i++)
		if(T.nodes[i].data == cur_e)
			break;
	
	if(T.nodes[i].parent == T.nodes[i+1].parent )
		return T.nodes[i+1].data;

	return NULL;
}



/*
* @description:返回左兄弟的值(這裡的左兄弟是指上一個與它有共同parent的節點)
*/
TElemType LeftSibling(PTree T,TElemType cur_e) {
	int i;

	for(i = 0;i < T.n; i++)
		if(T.nodes[i].data == cur_e)
			break;
	
	if(T.nodes[i-1].parent == T.nodes[i].parent )
		return T.nodes[i-1].data;

	return NULL;
}


/*
* @description:遍歷
*/
Status TreeTraverse(PTree T,Status (*Visit) (TElemType)) {
	int i;

	if(!TreeEmpty(T))
		for(i = 0;i <= T.n ; i++)
			Visit(T.nodes[i].data);
	return OK;
}

/*
* @description:列印元素
*/
Status PrintElem(TElemType elem) {
	printf("%c",elem);
	return OK;
}


/*
* @description:更加清晰的列印方式
*/
void PrintTree(PTree T) {
	int i;
	printf("該樹共有%d個節點\n",T.n);
	printf("Node		Parent\n");

	for(i = 0;i < T.n; i++) {
		printf("%c(%d)",Value(T,i),i);
		if(T.nodes[i].parent >= 0)
			printf("		%c(%d)\n",Value(T,T.nodes[i].parent),T.nodes[i].parent);
		else
			printf("		\n");
	}
}

測試檔案：

test.c

/*------------------------------------------------------------------------
	*file:test.c -->test file for ParentTree.c
	*date:10-4-2014
	*author:[email protected]
	*version:1.0
	*description:雙親表示法建樹和操作
-------------------------------------------------------------------------*/

#include <stdio.h>
#include "parenttree.h"

int main(int argc,char *argv[]) {
	PTree T;
	InitTree(&T);

	CreateTree(&T);

	PrintTree(T);
	printf("\n");

	TreeTraverse(T,PrintElem);

	Assign(&T,'5','0');

	printf("\nTreeEmpty:%d,TreeDepth:%d,Root:%c,Value:%c\n",TreeEmpty(T),TreeDepth(T),Root(T),Value(T,1));

	printf("Root:%c, Parent:%c, LeftChild:%c, RightSibling:%c, LeftSibling:%c\n",Root(T),Parent(T,'2'),LeftChild(T,'2'),RightSibling(T,'2'),LeftSibling(T,'3'));

	return 0;
}

涉及到了佇列的操作，完整的程式碼在這:GitHub

資料結構之雙親表示法建樹和操作

樹的雙親表示法假設以一組連續空間儲存樹的結點,同時在每個結點中,附設一個指示器指示其雙親結點到連結串列中的位置。也就是說,每個結點除了知道自己是誰以外,還知道它的雙親在哪裡。雙親表示法的資料儲存結構如下： #defin

樹的儲存結構：雙親表示法

#include<iostream> //樹結點 typedef struct{ char data;//資料域 int father;//雙親結點位置 }TreeNode; //樹連結串列 class Tree{ public: TreeNode e

資料結構之圖的遍歷和部分性質

無向圖和有向圖 1、無向圖中，任意兩個頂點之間都存在邊的話，就是無向完全圖。　含有n個頂點的無向完全圖有n×(n−1)2條邊。　有向圖中，若任意兩個頂點之間都存在方向互為相反的有向邊，則就是有向完全圖。　含有n個頂點的有向完全圖有n×(

C語言資料結構——孩子兄弟表示法

任意一棵樹，它的結點的第一個孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的。因此，我們設定兩個指標，分別指向該節點的第一個孩子和此結點的右兄弟。其中data是資料域，firstchild為指標域

資料結構——逆波蘭表示法

沒想到第一次寫資料結構就把我折騰死了呀~ 我看的是一本AOJ的書，然後以後的演算法也是跟著書的目錄來~ 題目的話會結合TOJ的一起寫，可以對照著看哦~ 這個逆波蘭表示法我就不多講了，AOJ我用的堆疊。在這裡我們可以運用棧的特點來實現字尾表示式，思路如下： 1.首先當遇

資料結構之雙向迴圈連結串列基本操作

#include<stdio.h>#include<malloc.h>#include<stdlib.h>#include<string.h>#define TRUE 1#define OK 1#define FALSE 0#define ERROR 0#def

資料結構之連結串列(Linked-List)及操作

一、資料結構之連結串列(Linked-List) 線性表是最常用的儲存結構，線性表的每個單元稱為元素，元素擁有一個數據及一個地址線性表有兩種物理儲存方式：順序儲存方式和鏈式儲存方式陣列是具有代表性的順序儲存方式的線性表，單鏈表是具有代表性的鏈式儲存方式的線性

資料結構之通用樹（使用連結串列實現樹的儲存結構，雙親孩子表示法）

樹是一種非線性的資料結構，可以使用連結串列組織樹的各個節點，描述樹的一些常用操作。雙親孩子表示法是指每個結點都有一個指向其雙親的指標，每個結點都有若干個指向其孩子的指標。標頭檔案： tree.h #ifndef __TREE_H__ #define __TREE_H__

資料結構-樹與森林-雙親表示法

以一組連續空間儲存結點，各結點附設指示器指示其雙親結點的位置（資料域加雙親下標域）。首先是輔助巨集： #define OK 1 #define ERROR 0 #define TRUE 1 #d

資料結構之樹的孩子連結串列表示法

#include"tree.h" const int max = 100; typedef char TElemType; typedef struct CTNode { int child; struct CTNode *next; }*ChildPtr,C

資料結構樹的雙親表示法

#include<iostream> #include<malloc.h> #include<stdlib.h> using namespace std; #define max 100 typedef char TElemType;

C語言資料結構——樹的雙親表示法

1、樹的雙親表示法： 2、/* bo6-4.c 樹的雙親表儲存(儲存結構由c6-4.h定義)的基本操作(14個) */ Status InitTree(PTree *T) { /* 操作結果: 構造空樹T */ (*T).n=0; r

資料結構之——關於單鏈表的頭插法和尾插法的程式碼和思路

頭插法思路：每次插入都在第一個節點之前，頭結點之後，那每次插入時的賦值就只要將頭結點的地址賦給插入的節點，然後將插入的節點的地址依次給後面節點就可以了。 1、定義一個要插入的節點q 2、q->data內給值e 3、q->next = p->nex

樹的儲存結構之雙親孩子表示法

已知給出的樹結構如下圖：用程式碼實現方式如下： /* 孩子表示法：浪費資源雙親孩子表示法：陣列和連結串列的結合 */ /* 1.雙親孩子表示法定義一個數結構,運用結構體指標的程式設計方式 2

資料結構之圖的陣列表示法

圖( Graph )是由頂點的有窮非空集合和頂點之間邊的集合組成,通常表示示為: G (V, E ) ,其中, G表示一個圖, V 是圖 G 中頂點的集合， E 是圖 G 中邊的集合。圖狀結構是一種比樹形結構更復雜的非線性結構。在樹

資料結構3—java 樹雙親表示法

假設以一組連續空間儲存樹的節點，同時在每個節點中，附設一個指示器指示其雙親結點到連結串列中的的位置，也就是說，每個結點知道自己是誰外，還知道雙親在哪裡。雙親表示法根據結點的parent指標很容易找到它的雙親結點，所以時間複雜度為O[1]，知道parent為

資料結構之伸展樹個人筆記伸展樹(一)之圖文解析和 C語言的實現

閱讀了skywang的伸展樹的講解，覺得講的很不錯，再次也推薦大家無論是新手還是老手都可以去閱讀下。 ----------------------------------------------------------------------------------------- 伸展樹(一)之圖文

資料結構之最大子列和

#include <stdlib.h> #include <stdio.h> int MaxSubseqSum(int a[],int N) { int i,ThisSum = 0,MaxSum = 0; &nb

真題2001 雙親表示法求樹中節點層次和樹高

題目:已知有n個結點的樹以雙親表示法儲存在一維陣列中。請設計一個演算法求樹中每個結點的層次和樹的高度，將求得的每個結點的層次儲存在一維陣列C中，並分析你所設計的演算法的時間複雜度。 int Depth(PTree t){ //編寫求雙親表示法表示的樹的深度的演算法

資料結構之——陣列和連結串列

1. 陣列 1.1 陣列為什麼從零編號？陣列名代表陣列的首地址，陣列的下標其實代表陣列中某個元素相對首地址的偏移量，陣列的第一個元素是零偏移，因此從 0 開始。上面其實也只是一個解釋， C 語言設計者用零開始編號，後來的各種語言也便紛紛效仿，因此就形成了這個習慣。 1

資料結構之雙親表示法建樹和操作

相關推薦