圖( Graph )是 由頂點的有窮非空集合和頂點之間邊的集合組成,通常表示示為: G (V, E ) ,其中, G表示一個圖, V 是圖 G 中頂點的集合， E 是 圖 G 中邊的集合 。

        上面是圖的概念，看不懂是吧，其實我也看不懂，呵呵。其實這個圖的相關概念也沒有那麼玄乎，建議找找離散數學的書看看，如果沒有相關的基礎是很難理解圖這個坑爹的玩意的，光一堆術語就能把人搞的暈頭轉向的，更別說程式碼中指標還指來指去的（如果實在沒時間可以看看這個

     資料結構中圖的基本操作如下：

（1） CreatGraph（G）輸入圖G 的頂點和邊，建立圖G 的儲存。
（2）DestroyGraph（G）釋放圖G 佔用的儲存空間。
（3）GetVex（G，v）在圖G 中找到頂點v，並返回頂點v 的相關資訊。
（4）PutVex（G，v，value）在圖G 中找到頂點v，並將value 值賦給頂點v。
（5）InsertVex（G，v）在圖G 中增添新頂點v。
（6）DeleteVex（G，v）在圖G 中，刪除頂點v 以及所有和頂點v 相關聯的邊或弧。
（7）InsertArc（G，v，w）在圖G 中增添一條從頂點v 到頂點w 的邊或弧。
（8）DeleteArc（G，v，w）在圖G 中刪除一條從頂點v 到頂點w 的邊或弧。
（9）DFSTraverse（G，v）在圖G 中，從頂點v 出發深度優先遍歷圖G。
（10）BFSTtaverse（G，v）在圖G 中，從頂點v 出發廣度優先遍歷圖G。
在一個圖中，頂點是沒有先後次序的，但當採用某一種確定的儲存方式儲存後，儲存結構中頂點的儲存次序構成了頂點之間的相對次序，這裡用頂點在
圖中的位置表示該頂點的儲存順序；同樣的道理，對一個頂點的所有鄰接點，採用該頂點的第i 個鄰接點表示與該頂點相鄰接的某個頂點的儲存順序，
在這種意義下，圖的基本操作還有：
（11）LocateVex（G，u）在圖G 中找到頂點u，返回該頂點在圖中位置。
（12）FirstAdjVex（G，v）在圖G 中，返回v 的第一個鄰接點。若頂點在G 中沒有鄰接頂點，則返回“空”。
（13）NextAdjVex（G，v，w）在圖G 中，返回v 的（相對於w 的）下一個鄰接頂點。若w 是v 的最後一個鄰接點，則返回“空”。
 

          圖的儲存結構有多種：陣列表示法，鄰接表，十字連結串列法，多重連結串列法，為了熟悉圖的運用我把每種表示方法都實現了一遍，有興趣的可以看看我後面更新的文章。當然這篇文章主要介紹陣列表示法，下面介紹陣列表示法。

        首先表示圖要就要表示圖中頂點的資訊又要表示頂點間的關係，考慮到圖是由頂點和邊或弧兩部分組成。合在一起比較困難,那就很自然地考慮到分兩個結構來分別儲存。頂點不分大小、主次,所以用一個一維陣列來儲存是很不錯的選擇。而邊或弧由於是頂點與頂點之間的關係, 一維搞不定,那就考慮用 一個二維陣列來儲存。於是我們的鄰接矩陣的方案就誕生了。圖的鄰接矩陣 ( Adjacency Matrix) 儲存方式是用兩個陣列來表示圈。一個一維陣列儲存圈中頂點資訊 ,一個二維陣列〈稱為鄰接矩陣)儲存圖中的邊或弧的資訊。

設圖G有n個頂點，則鄰接頂點是一個n * n的矩陣，具體定義如下（下面的是不帶權值的）：

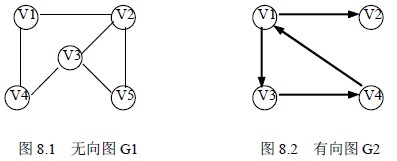
比較抽象，那麼看兩個例子：

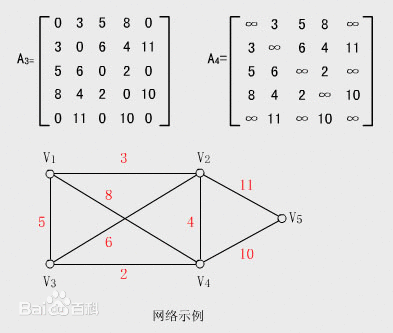
看完不帶權的再看帶權的：

大概看明白了，那麼我們來看陣列表示法的資料儲存結構：

#define INFINITY 65535 //表示無窮大-->在帶權的圖中用到，即網
#define MAX_VERTEX_NUM 20 //圖的最大定點數

#define MAX_INFO 20  //每條弧附帶資訊最大長度


//頂點關係型別
typedef int VRType;

//附加資訊型別
typedef char InfoType;

//頂點資料型別
typedef int VertexType;

//圖的種類:分別代表有向圖，有向網，無向圖，無向網
typedef enum {DG,DN,UDG,UDN} GraphKind;


typedef struct {
	VRType adj; //定點關係型別，對無權圖用1或0表示是否相鄰；對帶權圖，則為權值型別
	InfoType *info;	//附加資訊指標
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];


typedef struct {
	//頂點向量
	VertexType vexs[MAX_VERTEX_NUM];
	//鄰接矩陣
	AdjMatrix arcs;
	//圖的當前頂點數
	int vexnum;
	//圖的弧數
	int arcnum;
	//圖的種類
	GraphKind kind;
}MGraph;

上程式原始碼：

標頭檔案mgraph.h

/*---------------------------------------------------------------------------------
	* file:mgraph.h
	* date:10-9-2014
	* author:[email protected]
	* version:1.0
	* description:圖的陣列表示及基本操作
------------------------------------------------------------------------------------*/


#define TRUE 1
#define ERROR 0
#define OK 1
#define FALSE 0

#define INFINITY 65535 //表示無窮大-->在帶權的圖中用到，即網
#define MAX_VERTEX_NUM 20 //圖的最大定點數

#define MAX_INFO 20  //每條弧附帶資訊最大長度

typedef int Status;

//頂點關係型別
typedef int VRType;

//附加資訊型別
typedef char InfoType;

//頂點資料型別
typedef int VertexType;

//圖的種類:分別代表有向圖，有向網，無向圖，無向網
typedef enum {DG,DN,UDG,UDN} GraphKind;


typedef struct {
	VRType adj; //定點關係型別，對無權圖用1或0表示是否相鄰；對帶權圖，則為權值型別
	InfoType *info;	//附加資訊指標
}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];


typedef struct {
	//頂點向量
	VertexType vexs[MAX_VERTEX_NUM];
	//鄰接矩陣
	AdjMatrix arcs;
	//圖的當前頂點數
	int vexnum;
	//圖的弧數
	int arcnum;
	//圖的種類
	GraphKind kind;
}MGraph;


//陣列標記某元素是否被訪問過
int visited[MAX_VERTEX_NUM];

//建立圖,包括有無向圖，有無向網
Status CreateGraph(MGraph *G);

//建立無向圖
Status CreateUDG(MGraph *G);

//建立有向圖
Status CreateDG(MGraph *G);

//建立無向網
Status CreateUDN(MGraph *G);

//建立有向網
Status CreateDN(MGraph *G);

//返回某頂點在圖中的位置
int LocateVex(MGraph G,VertexType v);

//列印元素
Status PrintElem(VertexType elem);

//深度優先遍歷圖
Status DFSTraverse(MGraph G,Status (*Visit) (VertexType));

//深度優先遞迴遍歷
void DFS(MGraph G,int i,Status (*Visit) (VertexType));

//返回v的值
VertexType GetVex(MGraph G,int v);

//對v進行賦值
Status PutVex(MGraph *G,int v,VertexType value);

//返回v的第一個鄰接頂點
int FirstAdjVex(MGraph G,int v);

//w是v的鄰接點，返回v相對於w的下一個鄰接點
int NextAdjVex(MGraph G,int v,int w);

//插入一個頂點，但是不進行插入弧
Status InsertVex(MGraph *G,VertexType v);

//刪除一個頂點和相關的弧
Status DeleVex(MGraph *G,VertexType v);

//在頂點v,w間插入一段弧或邊
Status InsertArc(MGraph *G,VertexType v,VertexType w);

//刪除一段弧或邊，但是不刪除頂點
Status DeleArc(MGraph *G,VertexType v,VertexType w);

實現具體檔案MGraph.c

/*---------------------------------------------------------------------------------
	* file:MGraph.c
	* date:10-9-2014
	* author:[email protected]
	* version:1.0
	* description:圖的陣列表示及基本操作
------------------------------------------------------------------------------------*/


#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include "mgraph.h"
#include "linkqueue.h"



/*
* @description:建立圖,包括有向圖，無向圖，有向網，無向網
*/
Status CreateGraph(MGraph *G) {
	printf("please enter the kind of the graph(DG:0,DN:1,UDG:2,UDN:3):");
	scanf("%d",&(*G).kind);

	switch((*G).kind) {
		case UDG:
			return CreateUDG(G);
			break;
		case DG:
			return CreateDG(G);
		case UDN:
			return CreateUDN(G);
			break;
		case DN:
			return CreateDN(G);
			break;
		default:
			return ERROR;
	}
}	



/*
* @description:建立無向圖
* @more:分幾步來做
	1.確定頂點數/弧數
	2.確定各個頂點的值
	3.初始化鄰接矩陣
	4.確定鄰接矩陣
*/
Status CreateUDG(MGraph *G) {
	int i,j,k,infoflag,len;
	char c;
	//設定一個暫存區和一個臨時指標
	char str[MAX_INFO];
	char *info;

	VertexType v1,v2;

	len = 0;

	//確定頂點數/弧數
	printf("please enter vexnum, arcnum is info(1 or 0):");
	scanf("%d,%d,%d",&(*G).vexnum,&(*G).arcnum,&infoflag);

	//確定各個頂點的值
	printf("the value of each vertex:");
	for(i = 0;i < (*G).vexnum ; i++)
		scanf("%d,",&(*G).vexs[i]);
	
	//初始化鄰接矩陣
	for(i = 0; i < (*G).vexnum; i++) 
		for(j = 0;j < (*G).vexnum ; j++) {
			(*G).arcs[i][j].adj = 0;	//無向圖
			(*G).arcs[i][j].info = NULL;
		}


	//確定鄰接矩陣
	printf("please %d heads and %d tails:\n",(*G).vexnum,(*G).arcnum);
	for(k = 0; k < (*G).arcnum; k++) {
		scanf("%d,%d",&v1,&v2);
		
		i = LocateVex(*G,v1);
		j = LocateVex(*G,v2);

		if(i >= 0 && j >= 0)
			(*G).arcs[i][j].adj = (*G).arcs[j][i].adj = 1;	//無向圖,對稱矩陣
		//如果頂點有附帶資訊,則輸入並申請空間
		if(infoflag) {
			printf("please enter the info:");
			while( (c = getchar()) != '#')
				str[len++] = c;

			info = (char *) malloc(len * sizeof(char));
			str[len] = '\0';

			strcpy(info,str);

			(*G).arcs[i][j].info = (*G).arcs[j][i].info = info;
		}
	}

	(*G).kind = UDG;

	return OK;
}





/*
* @description:建立有向圖
* @more:分幾步來做
	1.確定頂點數/弧數
	2.確定各個頂點的值
	3.初始化鄰接矩陣
	4.確定鄰接矩陣
*/
Status CreateDG(MGraph *G) {
	int i,j,k,len,infoflag;
	VertexType v1,v2;

	char str[MAX_INFO];
	char *info;
	char c;

	//確定頂點數/弧數
	printf("please enter vexnum , arcnum and is info(1 or 0):");
	scanf("%d,%d,%d",&(*G).vexnum,&(*G).arcnum,&infoflag);

	//確定各個頂點的值
	printf("the value of each vertex:");
	for(i = 0;i < (*G).vexnum ; i++)
		scanf("%d,",&(*G).vexs[i]);
	
	//初始化鄰接矩陣
	for(i = 0; i < (*G).vexnum; i++) 
		for(j = 0;j < (*G).vexnum ; j++) {
			(*G).arcs[i][j].adj = 0;	//有向圖
			(*G).arcs[i][j].info = NULL;
		}


	//確定鄰接矩陣
	printf("please %d heads and %d tails:\n",(*G).vexnum,(*G).arcnum);
	for(k = 0; k < (*G).arcnum; k++) {
		scanf("%d,%d",&v1,&v2);
		
		i = LocateVex(*G,v1);
		j = LocateVex(*G,v2);

		if(i >= 0 && j >= 0)
			(*G).arcs[i][j].adj = 1;	//有向圖

		//如果頂點有附帶資訊,則輸入並申請空間
		if(infoflag) {
			printf("please enter the info:");
			while( (c = getchar()) != '#')
				str[len++] = c;

			info = (char *) malloc(len * sizeof(char));
			strcpy(info,str);

			(*G).arcs[i][j].info = info;
		}
	}

	(*G).kind = DG;

	return OK;
}




/*
* @description:建立有向網
*/

Status CreateDN(MGraph *G) {
	int i,j,k,len,infoflag,w;
	VertexType v1,v2;

	char str[MAX_INFO];
	char *info;
	char c;

	//確定頂點數/弧數
	printf("please enter vexnum , arcnum and is info(1 or 0):");
	scanf("%d,%d,%d",&(*G).vexnum,&(*G).arcnum,&infoflag);

	//確定各個頂點的值
	printf("the value of each vertex:");
	for(i = 0;i < (*G).vexnum ; i++)
		scanf("%d,",&(*G).vexs[i]);
	
	//初始化鄰接矩陣
	for(i = 0; i < (*G).vexnum; i++) 
		for(j = 0;j < (*G).vexnum ; j++) {
			(*G).arcs[i][j].adj = INFINITY;	//有向網
			(*G).arcs[i][j].info = NULL;
		}


	//確定鄰接矩陣
	printf("please %d heads and %d tails and weights:\n",(*G).vexnum,(*G).arcnum);
	for(k = 0; k < (*G).arcnum; k++) {
		scanf("%d,%d,%d",&v1,&v2,&w);
		
		i = LocateVex(*G,v1);
		j = LocateVex(*G,v2);

		if(i >= 0 && j >= 0)
			(*G).arcs[i][j].adj = w;	//有向圖

		//如果頂點有附帶資訊,則輸入並申請空間
		if(infoflag) {
			printf("please enter the info:");
			while( (c = getchar()) != '#')
				str[len++] = c;

			info = (char *) malloc(len * sizeof(char));
			strcpy(info,str);

			(*G).arcs[i][j].info = info;
		}
	}

	(*G).kind = DN;

	return OK;
}






/*
* @description:建立無向網
*/

Status CreateUDN(MGraph *G) {
	int i,j,k,len,infoflag,w;
	VertexType v1,v2;

	char str[MAX_INFO];
	char *info;
	char c;

	//確定頂點數/弧數
	printf("please enter vexnum , arcnum and is info(1 or 0):");
	scanf("%d,%d,%d",&(*G).vexnum,&(*G).arcnum,&infoflag);

	//確定各個頂點的值
	printf("the value of each vertex:");
	for(i = 0;i < (*G).vexnum ; i++)
		scanf("%d,",&(*G).vexs[i]);
	
	//初始化鄰接矩陣
	for(i = 0; i < (*G).vexnum; i++) 
		for(j = 0;j < (*G).vexnum ; j++) {
			(*G).arcs[i][j].adj = INFINITY;	//無向網
			(*G).arcs[i][j].info = NULL;
		}


	//確定鄰接矩陣
	printf("please heads,tails and weights:\n");
	for(k = 0; k < (*G).arcnum; k++) {
		scanf("%d,%d,%d",&v1,&v2,&w);
		
		i = LocateVex(*G,v1);
		j = LocateVex(*G,v2);

		if(i >= 0 && j >= 0)
			(*G).arcs[i][j].adj = (*G).arcs[j][i].adj = w;	//無向網

		//如果頂點有附帶資訊,則輸入並申請空間
		if(infoflag) {
			printf("please enter the info:");
			while( (c = getchar()) != '#')
				str[len++] = c;

			info = (char *) malloc(len * sizeof(char));
			strcpy(info,str);

			(*G).arcs[i][j].info = info;
		}
	}

	(*G).kind = UDN;

	return OK;
}







/*
* @description:判斷圖中是否存在v頂點，存在則返回該頂點在圖中的位置，否則返回其他資訊
*/
int LocateVex(MGraph G,VertexType v) {
	int i;

	for(i = 0;i < G.vexnum; i++)
		//匹配則返回
		if(G.vexs[i] == v)
			return i;

	return -1;
}


/*
* @description:深度優先遍歷圖
* @more:分為兩步
	1.一定要重新初始化訪問記錄陣列
	2.訪問沒有訪問過的頂點，並更新訪問記錄陣列
* @本函式中的第二個迴圈主要是為了保證每個頂點都能被訪問到
   而DFS中的迴圈是在尋找當前節點的相鄰節點來訪問
   關鍵的關鍵在於遞迴的理解-->廢話
*/
Status DFSTraverse(MGraph G,Status (*Visit) (VertexType)) {
	int i;
	//初始化訪問記錄陣列
	for(i = 0;i < G.vexnum; i++)
		visited[i] = FALSE;
	
	for(i = 0;i < G.vexnum ; i++) 
		if(!visited[i])
			DFS(G,i,Visit);

	return OK;
}



/*
* @description:深度優先遞迴遍歷
*/
void DFS(MGraph G,int i,Status (*Visit) (VertexType)) {
	int j,w;

	//標記
	visited[i] = TRUE;
	Visit(G.vexs[i]);

	for(w = FirstAdjVex(G,i); w >= 0; w = NextAdjVex(G,i,w))
		if(!visited[w])
			DFS(G,w,Visit);
}



/*
* @description:圖的廣度優先遍歷
* @more:值得注意的是廣度遍歷和樹中的層序遍歷採用的是同樣的思路-->採用佇列輔助
*/
Status BFSTraverse(MGraph G,Status (*Visit)(VertexType)) {
	LinkQueue Q;
	int i,w,u;
	
	//必須重新初始化訪問標記陣列
	for(i = 0;i < G.vexnum; i++) 
		visited[i] = FALSE;

	InitQueue(&Q);

	//用於確保每個頂點都會被訪問到
	for(i = 0;i < G.vexnum; i++) {
		if(!visited[i]) {
			Visit(G.vexs[i]);
			visited[i] = TRUE;

			//進隊
			EnQueue(&Q,i);

			while(!QueueEmpty(Q)) {
				//出隊一個元素
				DeQueue(&Q,&u);
				for(w = FirstAdjVex(G,u); w >= 0; w = NextAdjVex(G,u,w)) {
					if(!visited[w]) {
						visited[w] = TRUE;
						Visit(G.vexs[w]);
						EnQueue(&Q,w);
					}
				}
			}
		}
	}

	return OK;
}





/*
* @description:返回v的值
*/
VertexType GetVex(MGraph G,int v) {
	if(v >= G.vexnum || v < 0)
		exit(ERROR);

	return G.vexs[v];
}



/*
* @description:對v進行賦值
*/
Status PutVex(MGraph *G,int v,VertexType value) {
	if(v >= (*G).vexnum || v < 0)
		exit(ERROR);

	(*G).vexs[v] = value;

	return OK;
}

/*
* @description:返回v(序號)的第一個相鄰節點（序號）
*/
int FirstAdjVex(MGraph G,int v) {
	if(v > G.vexnum || v < 0)
		return -1;
	
	int i,j;

	j = 0;

	//如果是網
	if(G.kind == DN || G.kind == UDN )
		j = INFINITY;

	for(i = 0;i < G.vexnum; i++) 
		if(G.arcs[v][i].adj != j)
			return  i;

	return -1;
}

/*
* @description:w是v的相鄰節點，返回v相對w的下一個節點的序號，否則返回-1
*/
int NextAdjVex(MGraph G,int v,int w) {
	int i,j;
	
	j = 0;
	//如果為網
	if(G.kind == DN || G.kind == UDN)
		j = INFINITY;
	//兩頂點不相鄰
	if(G.arcs[v][w].adj == j)
		return -1;
	//從w之後的節點開始就可以
	for(i = w + 1; i < G.vexnum; i++) 
		if(G.arcs[v][i].adj != j)
			return i;

	return -1;
}


/*
* description:插入一個頂點，但是進行弧的插入，交給後面的插入弧操作進行
* @more:注意需要同時對鄰接矩陣行和列的跟新資訊,還有這裡的插入是直接在
	的位置進行插入，不指定位置
*/
Status InsertVex(MGraph *G,VertexType v) {
	int i;

	//進行賦值
	(*G).vexs[(*G).vexnum] = v;

	if((*G).kind == DN || (*G).kind == UDN)
		for(i = 0; i <= (*G).vexnum; i++) {
			//對行的鄰接關係進行初始化
			(*G).arcs[(*G).vexnum][i].adj = INFINITY;
			//對列的鄰接關係進行初始化
			(*G).arcs[i][(*G).vexnum].adj = INFINITY;

		}

	else 
		for(i = 0; i <= (*G).vexnum; i++) {
			//對行的鄰接關係進行初始化
			(*G).arcs[(*G).vexnum][i].adj = 0;
			//對列的鄰接關係進行初始化
			(*G).arcs[i][(*G).vexnum].adj = 0;

		}
	
	//對行進行初始化
	(*G).arcs[(*G).vexnum][i].info = NULL;
	//對列進行初始化
	(*G).arcs[i][(*G).vexnum].info = NULL;

	//圖的頂點數目加一
	(*G).vexnum++;

	return OK;
}




/*
* @description:刪除G中的頂點v其相關的弧(難點在於弧的刪除)
*/
Status DeleVex(MGraph *G,VertexType v) {
	int k,i,j;
	VRType m;

	m = 0;
	k = LocateVex(*G,v);

	if(k >= (*G).vexnum || k < 0)
		return ERROR;

	//圖的型別為網
	if((*G).kind == DN || (*G).kind == UDN)
		m = INFINITY;
	/*
	這裡主要是釋放弧的附帶資訊，如果是有向圖則為釋放入弧，
	如果是無向圖，由於其是對稱矩陣，釋放列或行就可
	*/
	for(i =0;i < (*G).vexnum; i++)
		if((*G).arcs[i][k].adj != m) {
			if((*G).arcs[i][k].info)
				free((*G).arcs[i][k].info);
			(*G).arcnum--;
		}

	//有向圖存在出弧
	if((*G).kind == DG || (*G).kind == DN) 
		for(i = 0;i < (*G).vexnum; i++)
			if((*G).arcs[k][i].adj != m) {
				if((*G).arcs[k][i].info)
					free((*G).arcs[k][i].info);

				(*G).arcnum--;
			}
	
	//將頂點陣列中的v之後的元素前移
	for(i = k + 1; i < (*G).vexnum; i++) 
		(*G).vexs[i-1] = (*G).vexs[i];
	
	//鄰接矩陣v之後的前移動
	for(i = 0;i < (*G).vexnum; i++)
		for(j = k + 1; j < (*G).vexnum ; j++)
			(*G).arcs[i][j-1] = (*G).arcs[i][j];

	//鄰接矩陣v之下的上移
	for(i = 0;i < (*G).vexnum; i++) 
		for(j = k +1; j < (*G).vexnum ; j++)
			(*G).arcs[j-1][i] = (*G).arcs[j][i];

	(*G).vexnum--;


	return OK;
}


/*
* @description:增添弧<v,w>，若是無向的，則還增添對稱弧<w,v>
		注意v,w已經存在圖中
*/
Status InsertArc(MGraph *G,VertexType v,VertexType w) {
	int v1,w1,infoflag,len;
	char str[MAX_INFO],c,*info;

	//獲取頂點對應位置
	v1 = LocateVex(*G,v);
	w1 = LocateVex(*G,w);
	len = 0;
	
	if(v1 < 0 || w1 < 0)
		return ERROR;
	
	
	if((*G).kind == DN || (*G).kind == UDN) {
		printf("please enter the weight:");
		scanf("%d",&(*G).arcs[v1][w1].adj);
	}
	else 
		(*G).arcs[v1][w1].adj = 1;

	printf("please make sure is info(1 or 0):");
	scanf("%d",&infoflag);

	//邊或弧有附帶資訊
	if(infoflag) {
		while( (c = getchar()) != '#') 
			str[len++] = c;

		info = (char *) malloc(len * sizeof(char));
		strcpy(info,str);
		(*G).arcs[v1][w1].info = info;
	}
	
	//注意如果是無向的，應該新增對稱邊<w,v)
	if((*G).kind == UDG || (*G).kind == UDN) {
		(*G).arcs[w1][v1].adj = (*G).arcs[v1][w1].adj;
		(*G).arcs[w1][v1].info = (*G).arcs[v1][w1].info;
	}

	(*G).arcnum++;

	return OK;
}


/*
* @description:刪除弧或邊<v,w>,如果圖為無向，則同時刪除其對稱弧或邊
*/
Status DeleArc(MGraph *G,VertexType v,VertexType w) {
	int v1,w1,m;

	v1 = LocateVex(*G,v);
	w1 = LocateVex(*G,w);
	m = 0;
	
	if(v1 < 0 || w1 <0)
		return ERROR;
	
	if((*G).kind == DN || (*G).kind == UDN)
		m = INFINITY;


	(*G).arcs[v1][w1].adj = m;

	if((*G).kind == UDN || (*G).kind == UDG)
		(*G).arcs[w1][v1].adj = (*G).arcs[v1][w1].adj;

	if((*G).arcs[v1][w1].info) {
		free((*G).arcs[v1][w1].info);

		if((*G).kind == UDN || (*G).kind == UDG)
			free((*G).arcs[w1][v1].info);
	}
	(*G).arcnum--;

	return OK;
}


/*
* @description:列印元素
*/
Status PrintElem(VertexType elem) {
	printf("%d",elem);
	return OK;
}

測試檔案：test.c

/*---------------------------------------------------------------------------------
	* file:MGraph.c
	* date:10-9-2014
	* author:[email protected]
	* version:1.0
	* description:圖的陣列表示及基本操作
------------------------------------------------------------------------------------*/


#include <stdio.h>
#include "mgraph.h"


int main(int argc,char *argv[]) {
	MGraph G;
	//建圖
	CreateGraph(&G);

	//深度優先遍歷圖
	DFSTraverse(G,PrintElem);
	printf("\n");
	BFSTraverse(G,PrintElem);
	printf("\n");
         /*
    測試用例結果：
    please enter the kind of the graph(DG:0,DN:1,UDG:2,UDN:3):2
    please enter vexnum, arcnum is info(1 or 0):8,8,0
    the value of each vertex:1,2,3,4,5,6,7,8
    please 8 heads and 8 tails:
    1,2
    1,3
    2,4
    2,5
    3,6
    3,7
    4,8 
    5,8
    12485367
    12345678

    */

 }

完整的原始碼可以看:GitHub

 本部落格持續更新，歡迎指正，互相學習。