原文：

我們可以用上面的方法二分求出任何一個線性遞推式的第n項，其對應矩陣的構造方法為：在右上角的(n-1)*(n-1)的小矩陣中的主對角線上填1，矩陣第n行填對應的係數，其它地方都填0。例如，我們可以用下面的矩陣乘法來二分計算f(n) = 4f(n-1) - 3f(n-2) + 2f(n-4)的第k項：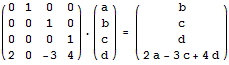

    利用矩陣乘法求解線性遞推關係的題目我能編出一卡車來。這裡給出的例題是係數全為1的情況。

根據原文得出的一個矩陣，然後算矩陣的高次冪。

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
#define Nnum 31
#define Mnum 31
#define LL __int64
#define MOD 7777777
using namespace std;
struct matrix
{
    LL mat[11][11];
    matrix(){
        memset(mat,0,sizeof(mat));
    }
};
int nn;
matrix mul(matrix A,matrix B)
{
    int i,j,k;
    matrix C;
    for(i=1;i<=nn;i++)
    {
        for(j=1;j<=nn;j++)
        {
            C.mat[i][j]=0;
            for(k=1;k<=nn;k++)
            {
                C.mat[i][j]=(C.mat[i][j]+A.mat[i][k]*B.mat[k][j])%MOD;
            }
        }
    }
    return C;
}
matrix powmul(matrix A,int k)
{
    matrix B;
    for(int i=1;i<=nn;i++)B.mat[i][i]=1;
    while(k)
    {
        if(k&1)B=mul(B,A);
        A=mul(A,A);
        k=k/2;
    }
    return B;
}
int main()
{
    int n,k,i,j;
    matrix A;
    matrix B;
    while(~scanf("%d%d",&k,&n))
    {
        nn=k;
        for(i=1;i<=k-1;i++)A.mat[i][i+1]=1;
        for(i=1;i<=k;i++)A.mat[k][i]=1;
        B.mat[0][1]=1;
        for(i=1;i<=k;i++)
            for(j=0;j<i;j++)
                B.mat[i][1]+=B.mat[j][1];
        A=powmul(A,n-1);
        B=mul(A,B);
        cout<<B.mat[1][1]<<endl;
    }
    return 0;
}