尤拉路徑,歐拉回路,並查集
1.1 定義
對於圖G,若存在一條路徑,經過G中每條邊有且僅有一次,稱這條路為尤拉路徑;如果存在一條迴路經過G每條邊有且僅有一次,稱這條迴路為歐拉回路。具有歐拉回路的圖成為尤拉圖。
1.2 判斷尤拉路徑是否存在的方法
有向圖:圖連通,且只有一個頂點出度大入度1,有一個頂點入度大出度1,其餘都是出度=入度。
無向圖:圖連通,奇度數的結點個數不多於2個,其餘都是偶數度的。
1.3 判斷歐拉回路是否存在的方法
有向圖:圖連通,且所有的頂點出度=入度。
無向圖:圖連通,且所有頂點都是偶數度。
定理一:如果連通無向圖  有
有 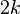 個奇頂點(奇定點數必然為偶數個),那麼它可以用
個奇頂點(奇定點數必然為偶數個),那麼它可以用  筆畫成,並且至少要用
筆畫成,並且至少要用  筆畫成。
筆畫成。
證明:將這 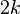 個奇頂點分成
個奇頂點分成  對後分別連起,則得到一個無奇頂點的連通圖。由上知這個圖是一個環,因此去掉新加的邊後至多成為
對後分別連起,則得到一個無奇頂點的連通圖。由上知這個圖是一個環,因此去掉新加的邊後至多成為  條尤拉路徑,因此必然可以用
條尤拉路徑,因此必然可以用  筆畫成。但是假設全圖可以分為
筆畫成。但是假設全圖可以分為  條尤拉路徑,則由定理一知,每條鏈中只有不多於兩個奇頂點,於是
條尤拉路徑,則由定理一知,每條鏈中只有不多於兩個奇頂點,於是  。因此必定要
。因此必定要  筆畫成。
筆畫成。
1.4 尤拉路徑與歐拉回路的題目
程式實現一般是如下過程:
(1).利用並查集判斷圖是否連通,即判斷p[i] < 0的個數,如果大於1,說明不連通。
(2).根據出度入度個數,判斷是否滿足要求。
(3).利用DFS輸出路徑。
/*函式過程中是維護一個連通圖點集A,初始時,每個單獨的結點都是一個連通圖,每加入一條邊,則將兩個連通圖合併在一起,組成一個新的連通圖。且對於每個連通圖,都有其代表結點x。陣列p[]用來記錄結點與所在連通圖代表結點之間的關係。*/
#include <iostream>
#include <stdio.h>
using namespace std;
const int maxv = 100 + 2;
int odds[maxv]; /* 頂點 */
int du[maxv]; /* 每個頂點的度數 */
int p[maxv]; /* 並查集陣列 */
bool used[maxv];
int scc[maxv]; /* scc個數 */
void init(int n) /*初始化陣列*/
{
for(int i = 0; i <= n; ++i)
{
odds[i] = 0;
p[i] = -1;
du[i] = 0;
used[i] = 0;
}
}
int utf_find(int x) /*本函式用來尋找結點x的代表結點。如果x尚未加入到陣列當中或者x即 */
{ /* 為自己以及其他結點的代表結點,p[x]<0. 此時返 回自己x;*/
if(0 <= p[x]) /*若結點x已被加入到集合A中且此時x的代表結點不是自己*/
{ /* 則遞迴呼叫尋找所在連通圖的代表結點x',特徵是p[x']<0。*/
p[x] = utf_find(p[x]);
return p[x];
}
return x;
}
void utf_union(int a, int b) //當加入一條邊的時候,是合併兩個連通圖。
{
int r1 = utf_find(a); //尋找新加入邊的兩個結點所在連通圖的代表結點是否一樣,
int r2 = utf_find(b); //一樣的話則為“冗餘邊”;否則即是將兩個連通圖連通在一塊。
if(r1 == r2)
return;
int n1 = p[r1]; //每個連通圖中結點的個數,連通圖A1中的結點個數為|n1|,連通圖A2中的結點個數為|n2|.
int n2 = p[r2];
if(n1 < n2) //A1中結點個數大於A2中結點個數
{ //將A2中的代表結點,再連結到A1中的代表結點。 P2: 給出n個單詞,如果一個單詞的尾和另一個單詞的頭字元相同,那麼這兩個單詞可以相連。求這n個單詞是否可以排成一列。應用尤拉圖,構圖:一個單詞的頭尾字幕分別作為頂點,每輸入一個word,則該word的頭指向word的尾有一條邊。記錄每個頂點的出入度。利用並查集先判斷是否為SCC。如果是的話再判斷奇數度節點為0個或者2個。
P3: 給出n個field以及m條邊連線這m個field,要求遍歷每條邊2次。求這樣的一條路徑。
若該field組成的圖是連通分量,那麼由於每條邊遍歷2次,即等效的每個結點的度均為偶數。故必然存在歐拉回路。此時只需對原圖作一次DFS,即可得到這樣的路徑。需要記錄下每次訪問的結點順序,重複訪問的也需打印出來。
P4: 給出一組單詞,如果一個單詞的尾和另一個單詞的頭字元相同,那麼這兩個單詞可以相連。問這組單詞能否排成一排,如果可以求出字典序最小的那個。構圖:單詞作為邊,單詞的首字元和尾字元作為結點。讀入一個單詞即新增一條邊。用鄰接連結串列法存邊。首先判斷圖是否連通,如果是,再判斷該圖能否構成尤拉路徑或者回路。如果是迴路,從字元'a'開始尋找,找到第一個存在的字母,從這個字母遍歷就行。如果是路徑,那麼必須從出度大於入度的那個結點開始訪問。由於這個題目要求的是最小字典序,然後考慮我們建立鄰接表時是採用頭插法,那麼我們將單詞從小到大排序,由於我們遍歷結點肯定是從小的結點開始的,這樣遍歷一個結點的鄰接邊的時候就會從大到小訪問這個結點的邊,無法滿足字典最小。所以從大到小排序,遍歷依node陣列為準,每次遍歷一條邊設定下標表示已訪問過。
