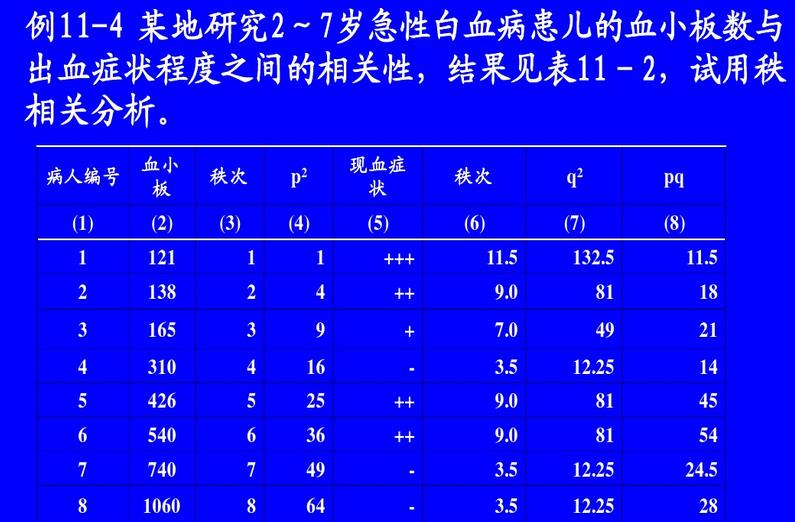
[秩相關] Spearman秩相關係數計算及假設檢驗
阿新 • • 發佈:2019-01-26
首先說明秩相關係數還有其他型別,比如kendal秩相關係數。
使用Pearson線性相關係數有2個侷限:
- 必須假設資料是成對地從正態分佈中取得的。
- 資料至少在邏輯範圍內是等距的。
對於更一般的情況有其他的一些解決方案,Spearman秩相關係數就是其中一種。Spearman秩相關係數是一種無引數(與分佈無關)檢驗方法,用於度量變數之間聯絡的強弱。在沒有重複資料的情況下,如果一個變數是另外一個變數的嚴格單調函式,則Spearman秩相關係數就是+1或-1,稱變數完全Spearman秩相關。注意這和Pearson完全相關的區別,只有當兩變數存線上性關係時,Pearson相關係數才為+1或-1。
對原始資料xi
















| 位置 | 原始X | 排序後 | 秩次 | 原始Y | 排序後 | 秩次 | 秩次差 |
| 1 | 12 | 546 | 5 | 1 | 78 | 6 | 1 |
| 2 | 546 | 45 | 1 | 78 | 46 | 1 | 0 |
| 3 | 13 | 32 | 4 | 2 | 45 | 5 | 1 |
| 4 | 45 | 13 | 2 | 46 | 6 | 2 | 0 |
| 5 | 32 | 12 | 3 | 6 | 2 | 4 | 1 |
| 6 | 2 | 2 | 6 | 45 | 1 | 3 | -3 |
對於上表資料,算出Spearman秩相關係數為:1-6*(1+1+1+9)/(6*35)=0.6571
如果原始資料中有重複值,則在求秩次時要以它們的平均值為準,比如:
| 原始X | 秩次 | 調整後的秩次 |
| 0.8 | 5 | 5 |
| 1.2 | 4 | (4+3)/2=3.5 |
| 1.2 | 3 | (4+3)/2=3.5 |
| 2.3 | 2 | 2 |
| 18 | 1 | 1 |
假設檢驗:
Spearman秩相關係數也應該進行假設檢驗,當n小於等於50時,用查表法,當n大於50時,計算統計量t的值,即用前面皮爾森相關係數假設檢驗中t值的計算方式。
對於上述資料,查閱秩相關係數檢驗的臨界值表
| n | 顯著水平 | |
| 0.05 | 0.01 | |
| 5 | 0.9 | 1 |
| 6 | 0.829 | 0.943 |
| 7 | 0.714 | 0.893 |
置信度=1-顯著水平。上表顯示在n=6的時候,當spearman秩相關係數>=0.829時我們有95%的置信度認為兩個隨機變數相關,當spearman秩相關係數>=0.943時我們有99%的置信度認為兩個隨機變數相關。由於0.6571<0.829,即置信度達不到95%,所以我們不能認為X和Y相關。
例項: