簡單易學的機器學習演算法——SVD奇異值分解
阿新 • • 發佈:2019-01-26
一、SVD奇異值分解的定義
假設是一個
的矩陣,如果存在一個分解:
其中為
的酉矩陣,
為
的半正定對角矩陣,
為
的共軛轉置矩陣,且為
的酉矩陣。這樣的分解稱為
的奇異值分解,
對角線上的元素稱為奇異值,
稱為左奇異矩陣,
稱為右奇異矩陣。
二、SVD奇異值分解與特徵值分解的關係
特徵值分解與SVD奇異值分解的目的都是提取一個矩陣最重要的特徵。然而,特徵值分解只適用於方陣,而SVD奇異值分解適用於任意的矩陣,不一定是方陣。
這裡,和
是方陣,
和
為單位矩陣,
為
的特徵向量,
為
的特徵向量。
和
的特徵值為
的奇異值的平方。
三、SVD奇異值分解的作用和意義
奇異值分解最大的作用就是資料的降維,當然,還有其他很多的作用,這裡主要討論資料的降維,對於取其前
五、實驗的模擬
我們在手寫體上做實驗,原始矩陣為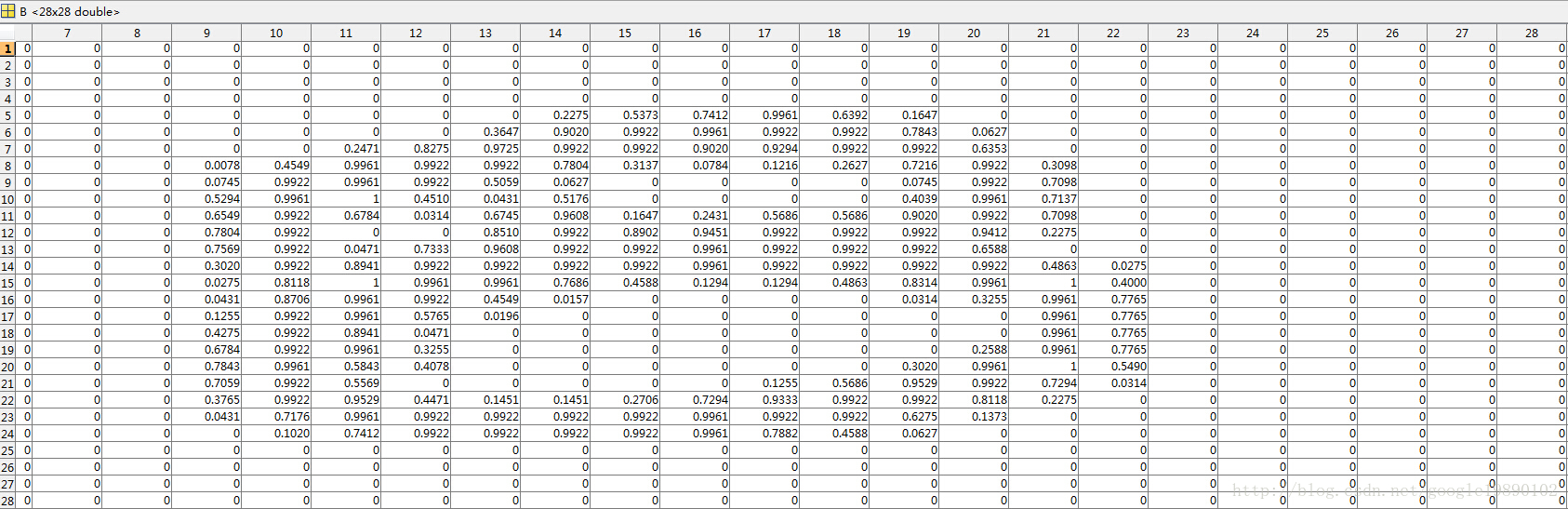
原始矩陣 對應的影象為

對應影象 經過SVD分解後的奇異值矩陣為
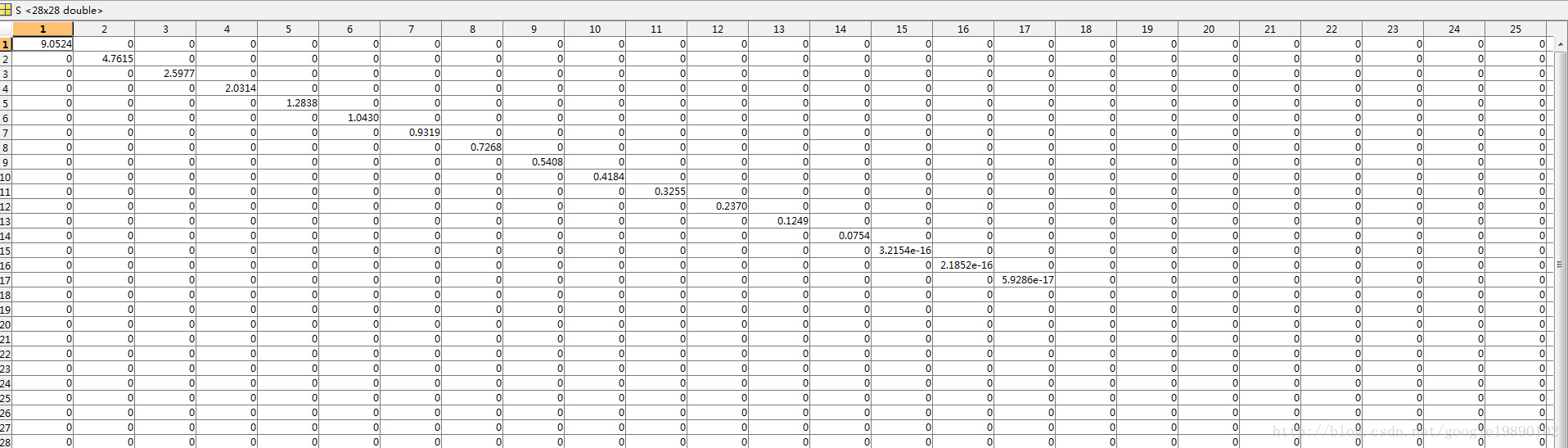
部分奇異值矩陣 取前14個非零奇異值
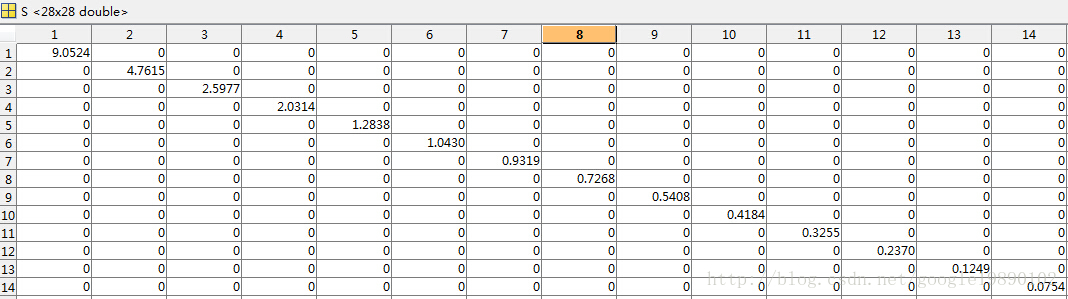
前14個非零奇異值 還原原始矩陣B,還原後的影象為

還原後的影象 對比影象

對比影象 MATLAB程式碼
%% 測試奇異值分解過程 load data.mat;%該檔案是做好的一個手寫體的圖片 B = zeros(28,28);%將行向量重新轉換成原始的圖片 for i = 1:28 j = 28*(i-1)+1; B(i,:) = A(1,j:j+27); end %進行奇異值分解 [U S V] = svd(B); %選取前面14個非零奇異值 for i = 1:14 for j = 1:14 S_1(i,j) = S(i,j); end end %左奇異矩陣 for i = 1:28 for j = 1:14 U_1(i,j) = U(i,j); end end %右奇異矩陣 for i = 1:28 for j = 1:14 V_1(i,j) = V(i,j); end end B_1 = U_1*S_1*V_1'; %同時輸出兩個圖片 subplot(121);imshow(B); subplot(122);imshow(B_1);
