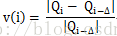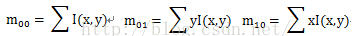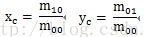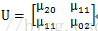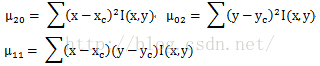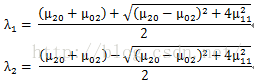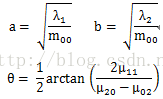最大穩定極值區域(MSER)檢測
Lowe和Bay提出的SIFT和SURF演算法高效實現了具有尺度和旋轉不變性的特徵檢測,但這些特徵不具有仿射不變性。
區域檢測針對各種不同形狀的影象區域,通過對區域的旋轉和尺寸歸一化,可以實現仿射不變性。
MSER(Maximally Stable Extrernal Regions)是區域檢測中影響最大的演算法
1. 原理
MSER基於分水嶺的概念:對影象進行二值化,二值化閾值取[0, 255],這樣二值化影象就經歷一個從全黑到全白的過程(就像水位不斷上升的俯瞰圖)。在這個過程中,有些連通區域面積隨閾值上升的變化很小,這種區域就叫MSER。
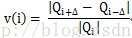
顯然,這樣檢測得到的MSER內部灰度值是小於邊界的,想象一副黑色背景白色區域的圖片,顯然這個區域是檢測不到的。因此對原圖進行一次MSER檢測後需要將其反轉,再做一次MSER檢測,兩次操作又稱MSER+和MSER-
2. 演算法步驟
從上節可以看到,MSER的基本思路很簡單,但編碼實現是很需要演算法和程式設計技巧的
以下演算法步驟基於改進的分水嶺演算法:注水的地方固定,只有當該處的溝壑水漫出來後才能注入到另一個溝壑
此外,為方便程式設計,面積變化的計算方式也從雙邊改為單邊檢測,即
1、初始化棧和堆,棧用於儲存組塊(組塊就是區域,就相當於水面,水漫過的地方就會出現水面,水面的高度就是影象的灰度值,因此用灰度值來表示組塊的值),堆用於儲存組塊的邊界畫素,相當於水域的岸邊,岸邊要高於水面的,因此邊界畫素的灰度值一定不小於它所包圍的區域(即組塊)的灰度值。首先向棧內放入一個虛假的組塊,當該組塊被彈出時意味著程式的結束;
2、把影象中的任意一個畫素(一般選取影象的左上角畫素)作為源畫素,標註該畫素為已訪問過,並且把該畫素的灰度值作為當前值。這一步相當於往源畫素這一地點注水;
3、向棧內放入一個空組塊,該組塊的值是當前值;
4、按照順序搜尋當前值的4-領域內剩餘的邊緣,對於每一個鄰域,檢查它是否已經被訪問過,如果沒有,則標註它為已訪問過並檢索它的灰度值,如果灰度值不小於當前值,則把它放入用於存放邊界畫素的堆中。另一方面,如果領域灰度值小於當前值,則把當前值放入堆中,而把領域值作為當前值,並回到步驟3;
5、累計棧頂組塊的畫素個數,即計算區域面積,這是通過迴圈累計得到的,這一步相當於水面的飽和;
6、彈出堆中的邊界畫素。如果堆是空的,則程式結束;如果彈出的邊界畫素的灰度值等於當前值,則回到步驟4;
7、從堆中得到的畫素值會大於當前值,因此我們需要處理棧中所有的組塊,直到棧中的組塊的灰度值大於當前邊界畫素灰度值為止。然後回到步驟4。
至於如何處理組塊,則需要進入處理棧子模組中,傳入該子模組的值為步驟7中從堆中提取得到的邊界畫素灰度值。子模組的具體步驟為:
1)、處理棧頂的組塊,即根據公式2計算最大穩定區域,判斷其是否為極值區域;
2)、如果邊界畫素灰度值小於距棧頂第二個組塊的灰度值,那麼設棧頂組塊的灰度值為邊界畫素灰度值,並退出該子模組。之所以會出現這種情況,是因為在棧頂組塊和第二個組塊之間還有組塊沒有被檢測處理,因此我們需要改變棧頂組塊的灰度值為邊界畫素灰度值(相當於這兩層的組塊進行了合併),並回到主程式,再次搜尋組塊;
3)、彈出棧頂組塊,並與目前棧頂組塊合併;
4)、如果邊界畫素灰度值大於棧頂組塊的灰度值,則回到步驟1。
注:MSER演算法引數較多,預設值如圖3-1所示(摘自《影象區域性不變性特徵與描述》)
圖3-1. MSER引數標準取值
3. MSER區域擬合
為了進一步對MSER得到的不規則區域進行描述和處理,需要對其進行橢圓擬合(橢圓可以反映區域的位置、尺寸、方向)
1)橢圓的重心
對區域內的每個點,計算整個區域的幾何0階矩和幾何一階矩
得到整個區域的重心位置
2) 橢圓的長半軸、短半軸、角度(長半軸與x軸順時針)
計算中心二階矩
其中
計算該二階矩的兩個特徵值,有
於是可以分別得到其長半軸、短半軸、角度
4. 程式碼
目前MSER的程式碼實現有3:OpenCV(目前操作手冊上還沒有這個介面的介紹)、IDIAP的實現(C++)、VLFeat的實現(C)
其中OpenCV的程式碼解讀可參考Opencv2.4.9原始碼分析——MSER,其和IDIAP的實現都嚴格遵循著上一節的演算法步驟,
IDIAP的版本只有一個mser.cpp和mser.h,很乾淨便於移植(如果是C實現的就更好了),其在Github上聲稱比VLFeat快幾倍。
VLFeat是一個C實現的影象特徵檢測演算法庫,包含了SIFT、HOG、K-Means、MSER等演算法
貼上IDIAP和OpenCV實現的呼叫程式碼
#IDIAP
clock_t start = clock();
_MSER mser8(5, 0.0005, 0.5, 0.25, 0.2, true);
_MSER mser4(5, 0.0005, 0.5, 0.25, 0.2, false);
std::vector<_MSER::Region> regions[2];
mser8(imgBuffer, grayImg.cols, grayImg.rows, regions[0]);
// Invert the pixel values
for (int i = 0; i < grayImg.cols*grayImg.rows; ++i)
imgBuffer[i] = ~imgBuffer[i];
mser4(imgBuffer, grayImg.cols, grayImg.rows, regions[1]);
clock_t stop = clock();
for (int i = 0; i < 2; ++i)
for (int j = 0; j < regions[i].size(); ++j)
//IDIAP自己實現的橢圓擬合函式
drawEllipse(regions[i][j], img.cols, img.rows, 3, imgBufferRGB, colors[i]);#OpenCV
cv::MSER ms(5, 0.0005, 1440);
std::vector<std::vector<cv::Point>> regions;
clock_t start = clock();
ms(grayImg, regions, cv::Mat());
clock_t stop = clock();
for (int i = 0; i < regions.size(); i++)
cv::ellipse(img, cv::fitEllipse(regions[i]), cv::Scalar(0, 0, 255));從實際效果來看,執行效率 OpenCV > IDIAP,VLFeat沒測試
圖4-1左是IDIAP的實現效果(引數與程式碼中一致),右是OpenCV的實現效果(其餘引數隱含在features2d.hpp內)
圖4-1. MSER檢測