優化演算法——模擬退火演算法
模擬退火演算法原理
爬山法是一種貪婪的方法,對於一個優化問題,其大致影象(影象地址)如下圖所示:
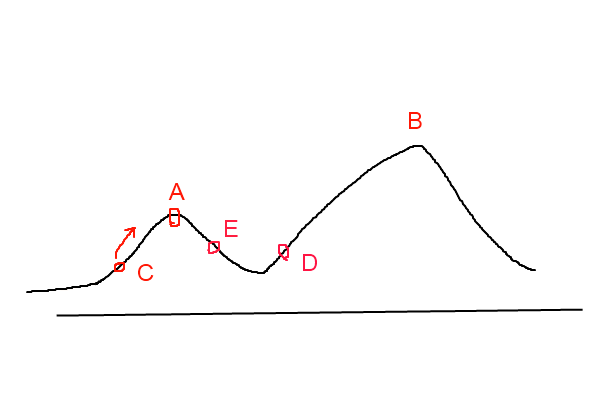
其目標是要找到函式的最大值,若初始化時,初始點的位置在
模擬退火演算法(Simulated Annealing, SA)的思想借鑑於固體的退火原理,當固體的溫度很高的時候,內能比較大,固體的內部粒子處於快速無序運動,當溫度慢慢降低的過程中,固體的內能減小,粒子的慢慢趨於有序,最終,當固體處於常溫時,內能達到最小,此時,粒子最為穩定。模擬退火演算法便是基於這樣的原理設計而成。
模擬退火演算法從某一較高的溫度出發,這個溫度稱為初始溫度,伴隨著溫度引數的不斷下降,演算法中的解趨於穩定,但是,可能這樣的穩定解是一個區域性最優解,此時,模擬退火演算法中會以一定的概率跳出這樣的區域性最優解,以尋找目標函式的全域性最優解。如上圖中所示,若此時尋找到了
模擬退火演算法
模擬退火演算法過程
(1)隨機挑選一個單元
(2)若
若
式中
(3)轉第(1)步繼續執行,知道達到平衡狀態為止。
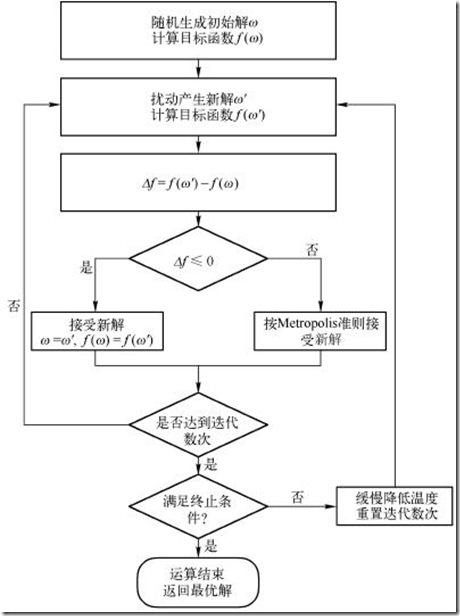
模擬退火演算法流程
模擬退火演算法的Java實現
求解函式最小值問題:
其中,
Java程式碼
package sa;
/**
* 實現模擬退火演算法
* @author zzy
*Email: 最後的結果
最優解為:1.733360963664572E-16
相關推薦
【電腦科學】【2016.10】多目標優化的模擬退火演算法研究
本文為英國埃克塞特大學(作者:Kevin Ian Smith)的電腦科學博士論文,共137頁。 許多應用領域的計算優化問題都歸結為多目標優化問題,從而達到最小化或最大化的目的。如果(通常情況下)這些目標都是相互競爭的目標,則優化的目的是找出一組合適的解決方
優化演算法——模擬退火演算法
模擬退火演算法原理 爬山法是一種貪婪的方法,對於一個優化問題,其大致影象(影象地址)如下圖所示: 其目標是要找到函式的最大值,若初始化時,初始點的位置在C處,則會尋找到附近的區域性最大值A點處,由於A點出是一個區域性最大值點,故對於爬山法來講,
優化演算法1:模擬退火演算法思想解析
1.演算法簡介 模擬退火演算法得益於材料的統計力學的研究成果。統計力學表明材料中粒子的不同結構對應於粒子的不同能量水平。在高溫條件下,粒子的能量較高,可以自由運動和重新排列。在低溫條件下,粒子能量較低。如果從高溫開始,非常緩慢地降溫(這個過程被稱為退火),粒子
集體智慧程式設計——優化搜尋演算法:爬山法,模擬退火演算法,遺傳演算法-Python實現
在優化問題中,有兩個關鍵點 代價函式:確定問題的形式和規模之後,根據不同的問題,選擇要優化的目標。如本文涉及的兩個問題中,一個優化目標是使得航班選擇最優,共計12個航班,要使得總的票價最少且每個人的等待時間之和最小。第二個問題是學生選擇宿舍的問題,每個學生可
現代優化演算法探究 模擬退火演算法
相較於完全貪心的單點爬山演算法,模擬退火用概率接受新解的方式,對貪心法容易陷入區域性最優解的缺陷進行了改進,是一種常用的在大的搜尋空間中逼近全域性最優解的元啟發式方法。這裡先大致描述演算法。然後先用一個簡單的求函式最小值例子,解釋我寫的c++模擬退火演算法模板的基本使用,之後
使用模擬退火演算法優化 Hash 函式
# 背景 現有個處理股票行情訊息的系統,其架構如下: 由於資料量巨大,系統中啟動了 15 個執行緒來消費行情訊息。訊息分配的策略較為簡單:對 symbol 的 hashCode 取模,將訊息分配給其中一個執行緒進行處理。 經過驗證,每個執行緒分配到的 symbol 數量較為均勻,於是系統愉快地上線
MATLAB模擬退火演算法模板
為了參加國賽,這幾天學了模擬退火演算法,整理下當做模板方便國賽的時候用。 模擬退火用於處理最優化問題,可以求出當目標函式取得最小值時的決策變數的值。 在編寫程式時需要根據具體問題設計演算法,演算法描述為: (1)解空間(初始解) (2)目標函式 (3)新解的產生 &nbs
模擬退火演算法案例
2018年的華為軟體精英挑戰賽題目簡介:給出華為雲虛擬機器過去的租借數量歷史資料,用以訓練模型並預測下一個時間段裡的虛擬機器租借數量,然後把這些預測得到的虛擬機器裝填進一定規格的物理機中,即分為預測和裝填兩個部分。 總結一下裝填部分使用的模擬退火演算法: 演算法原理 裝
HDU 3007 模擬退火演算法
Buried memory Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 4067
深度學習 --- 模擬退火演算法詳解(Simulated Annealing, SA)
上一節我們深入探討了,Hopfield神經網路的性質,介紹了吸引子和其他的一些性質,而且引出了偽吸引子,因為偽吸引子的存在導致Hopfield神經網路正確率下降,因此本節致力於解決偽吸引子的存在。在講解方法之前我們需要再次理解一些什麼是偽吸引子,他到底是如何產生的? 簡單來說說就是網路動態轉
模擬退火演算法理論+Python解決函式極值+C++實現解決TSP問題
簡述 演算法設計課這周的作業: 趕緊寫了先,不然搞不完了。 文章目錄 簡述 演算法理論部分 變數簡單分析 從狀態轉移概率到狀態概率 推導 理解當溫度收斂到接近0的時候,收斂到結果 理論
模擬退火演算法詳解
轉載自http://cighao.com/2015/12/03/introduction-of-SA/ 1. 簡介 模擬退火演算法 (Simulated Annealing,SA) 最早的思想是由 N. Metropolis 等人於1953年提出。1983年, S. Kirkpatr
模擬退火演算法
模擬退火演算法是一種求函式最小值點的隨機演算法,最近工作中要用到優化演算法,因此研究了一下這個比較簡單的演算法。模擬退火最基本的思想來源於金屬退火過程,在退火過程中,熱運動的原子逐漸凍結在勢能最低的位置,從而保證了整塊金屬晶格結構的一致性,達到最佳效能。模擬退火演算法的基本步驟如下: 1. 確定搜尋起始點x
啟發式優化演算法:退火演算法
一. 爬山演算法 ( Hill Climbing ) 介紹模擬退火前,先介紹爬山演算法。爬山演算法是一種簡單的貪心搜尋演算法,該演算法每次從當前解的臨近解空間中選擇一個最優解作為當前解,直到達到一個區域性最優解。 爬山演算法實現很簡單,其主要缺點是會陷入區域性最優解,而不一定能搜尋到全域
2899 Strange fuction【爬山演算法 || 模擬退火】
Time limit 1000 ms Memory limit 32768 kB Now, here is a fuction: $F(x) = 6 * x7+8*x6+7x3+5*x2-yx (0 <= x <=100) $ Can you fin
2069 Super Star【爬山演算法 || 模擬退火】
Time limit 1000 ms Memory limit 65536 kB During a voyage of the starship Hakodate-maru (see Problem 1406), researchers found stra
模擬退火演算法2
著名的模擬退火演算法,它是一種基於蒙特卡洛思想設計的近似求解最優化問題的方法。 一點歷史——如果你不感興趣,可以跳過 美國物理學家 N.Metropolis 和同仁在1953年發表研究複雜系統、計算其中能量分佈的文章,他們使用蒙特卡羅模擬法計算多分子系統
模擬退火演算法與C語言實現(TSP問題)
1簡介: 模擬退火來自冶金學的專有名詞退火。退火是將材料加熱後再經特定速率冷卻,目的是增大晶粒的體積,並且減少晶格中的缺陷。材料中的原子原來會停留在使內能有區域性最小值的位置,加熱使能量變大,原子會離開原來位置,而隨機在其他位置中移動。退火冷卻時速度較慢,使得原子有較多可能
人工智慧實驗——隨機重啟爬山法,模擬退火演算法,遺傳演算法求解N皇后問題
一、爬山法 爬山法就是完全的貪心演算法,每一步都選最優位置,可能只能得到區域性最優解。本實驗對普通爬山法進行了簡單的優化,採用了傳統爬山法的變種——隨機重啟爬山法,當爬山步數超過一定值時,會重新打亂棋盤,重新“爬山”。 適應度函式:衝突皇后的總對數 “爬山”:每一步就是
[work] 演算法學習筆記 (爬山法,模擬退火演算法,遺傳演算法)
在優化問題中,有兩個關鍵點 代價函式 確定問題的形式和規模之後,根據不同的問題,選擇要優化的目標。如本文涉及的兩個問題中,一個優化目標是使得航班選擇最優,共計12個航班,要使得總的票價最少且每個人的等待時間之和最小。第二個問題是學生選擇宿舍的問題,每個學生可以實現填報