A. Modular Exponentiation time limit per test 1 second memory limit per test 256 megabytes

The following problem is well-known: given integers n and m, calculate

,

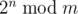where 2n = 2·2·...·2 (n factors), and 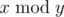 denotes the remainder of division of x by y.

You are asked to solve the "reverse" problem. Given integers n

 and m, calculate

. Input

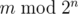The first line contains a single integer n (1 ≤ n ≤ 108).

The second line contains a single integer m (1 ≤ m ≤ 108).

Output

Output a single integer — the value of .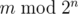

Examples input

4
42

output

10

input

1
58

output

0

input

98765432
23456789

output

23456789

Note

In the first example, the remainder of division of 42 by 24 = 16 is equal to 10.

In the second example, 58 is divisible by 21 = 2 without remainder, and the answer is 0.

題目分析：2^n很快就超過n了

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
int n, m;

int main() {
    scanf("%d %d", &n, &m);
    if (n >= 31) {
        printf("%d\n", m);
    } else {
        int ans = 1;
        for (int i = 1; i <= n; i++) {
            ans *= 2;
        }
        printf("%d\n", m % ans);
    }
}
 

B. Christmas Spruce time limit per test 1 second memory limit per test 256 megabytes

Consider a rooted tree. A rooted tree has one special vertex called the root. All edges are directed from the root. Vertex u is called a child of vertex v and vertex v is called a parent of vertex u if there exists a directed edge from v to u. A vertex is called a leaf if it doesn't have children and has a parent.

Let's call a rooted tree a spruce if its every non-leaf vertex has at least 3 leaf children. You are given a rooted tree, check whether it's a spruce.

The definition of a rooted tree can be found here.

Input

The first line contains one integer n — the number of vertices in the tree (3 ≤ n ≤ 1 000). Each of the next n - 1 lines contains one integer pi (1 ≤ i ≤ n - 1) — the index of the parent of the i + 1-th vertex (1 ≤ pi ≤ i).

Vertex 1 is the root. It's guaranteed that the root has at least 2 children.

Output

Print "Yes" if the tree is a spruce and "No" otherwise.

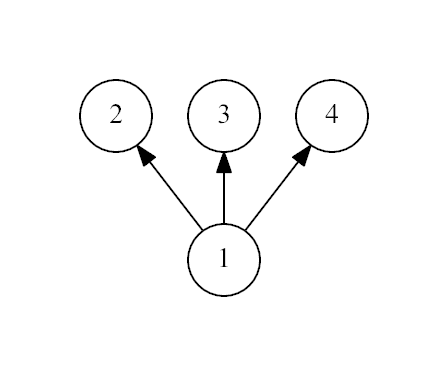
Examples input

4
1
1
1

output

Yes

input

7
1
1
1
2
2
2

output

No

input

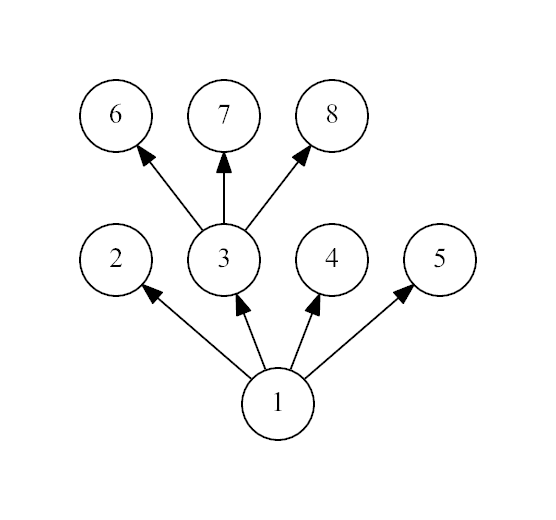
8
1
1
1
1
3
3
3

output

Yes

Note

The first example:

The second example:

It is not a spruce, because the non-leaf vertex 1 has only 2 leaf children.

The third example:

題目大意：判斷一棵有根樹是否滿足每個非葉子節點的孩子中至少包含3個葉子節點 題目分析：記錄點的出度

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
int const MAX = 1005;
int n, ind[MAX];
int cnt, head[MAX];

struct EDGE{
    int to, nxt;
}e[MAX];

void add(int u, int v) {
    e[cnt].to = v;
    e[cnt].nxt = head[u];
    head[u] = cnt ++;
}

int main() {
    scanf("%d", &n);
    int v;
    cnt = 0;
    memset(head, -1, sizeof(head));
    for (int u = 2; u <= n; u++) {
        scanf("%d", &v);
        add(v, u);
        ind[v] ++;
    }
    bool flag = true;
    for (int u = 1; u <= n; u++) {
        if (ind[u] > 0 && ind[u] < 3) {
            flag = false;
        }
        if (ind[u] >= 3) {
            int tmp = ind[u];
            for (int i = head[u]; i != -1; i = e[i].nxt) {
                v = e[i].to;
                if (ind[v] >= 3) {
                    tmp --;
                }
            }
            if (tmp < 3) {
                flag = false;
                break;
            }
        }
    }
    printf("%s\n", flag ? "Yes" : "No");
}

C. Party Lemonade time limit per test 1 second memory limit per test 256 megabytes

A New Year party is not a New Year party without lemonade! As usual, you are expecting a lot of guests, and buying lemonade has already become a pleasant necessity.

Your favorite store sells lemonade in bottles of n different volumes at different costs. A single bottle of type i has volume 2i - 1 liters and costs ci roubles. The number of bottles of each type in the store can be considered infinite.

You want to buy at least L liters of lemonade. How many roubles do you have to spend?

Input

The first line contains two integers n and L (1 ≤ n ≤ 30; 1 ≤ L ≤ 109) — the number of types of bottles in the store and the required amount of lemonade in liters, respectively.

The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 109) — the costs of bottles of different types.

Output

Output a single integer — the smallest number of roubles you have to pay in order to buy at least L liters of lemonade.

Examples input

4 12
20 30 70 90

output

150

input

4 3
10000 1000 100 10

output

10

input

4 3
10 100 1000 10000

output

30

input

5 787787787
123456789 234567890 345678901 456789012 987654321

output

44981600785557577

Note

In the first example you should buy one 8-liter bottle for 90 roubles and two 2-liter bottles for 30 roubles each. In total you'll get 12 liters of lemonade for just 150 roubles.

In the second example, even though you need only 3 liters, it's cheaper to buy a single 8-liter bottle for 10 roubles.

In the third example it's best to buy three 1-liter bottles for 10 roubles each, getting three liters for 30 roubles.

題目大意：n個物品，第i個物品體積為2^(i-1)，花費為ci，求總體積至少為L的最少花費 題目分析：若c[i] > 2*c[i-1]，那麼要買2^(i-1)體積肯定是買兩個c[i-1]更優，因此可以先預處理一下，考慮將L轉為二進位制，為1的位是必須買的，但是如果為0的位花費更少，其對應的體積顯然又要比先前已買的總體積要大 => (Sn=2^n-1 < an = 2^(n+1-1))，因此可以直接買這個體積更大，花費更小的

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#define ll long long 
using namespace std;
int const MAX = 50;
ll c[MAX], L;
int n;

int main() {
    cin >> n >> L;
    for (int i = 0; i < n; i++) {
        cin >> c[i];
    }
    for (int i = 1; i <= 30; i++) {
        c[i] = min(c[i], c[i - 1] << 1);
        if (i >= n) {
            c[i] = c[i - 1] << 1;
        }
    }
    ll ans = 0;
    for (int i = 0; i <= 30; i++) {
        ans = ((1 << i) & L) ? ans + c[i] : min(ans, c[i]);
    }
    cout << ans << endl;
}

D. Too Easy Problems time limit per test 2 seconds memory limit per test 256 megabytes

You are preparing for an exam on scheduling theory. The exam will last for exactly T milliseconds and will consist of n problems. You can either solve problem i in exactly ti milliseconds or ignore it and spend no time. You don't need time to rest after solving a problem, either.

Unfortunately, your teacher considers some of the problems too easy for you. Thus, he assigned an integer ai to every problem i meaning that the problem i can bring you a point to the final score only in case you have solved no more than ai problems overall (including problem i).

Formally, suppose you solve problems p1, p2, ..., pk during the exam. Then, your final score s will be equal to the number of values of jbetween 1 and k such that k ≤ apj.

You have guessed that the real first problem of the exam is already in front of you. Therefore, you want to choose a set of problems to solve during the exam maximizing your final score in advance. Don't forget that the exam is limited in time, and you must have enough time to solve all chosen problems. If there exist different sets of problems leading to the maximum final score, any of them will do.

Input

The first line contains two integers n and T (1 ≤ n ≤ 2·105; 1 ≤ T ≤ 109) — the number of problems in the exam and the length of the exam in milliseconds, respectively.

Each of the next n lines contains two integers ai and ti (1 ≤ ai ≤ n; 1 ≤ ti ≤ 104). The problems are numbered from 1 to n.

Output

In the first line, output a single integer s — your maximum possible final score.

In the second line, output a single integer k (0 ≤ k ≤ n) — the number of problems you should solve.

In the third line, output k distinct integers p1, p2, ..., pk (1 ≤ pi ≤ n) — the indexes of problems you should solve, in any order.

If there are several optimal sets of problems, you may output any of them.

Examples input

5 300
3 100
4 150
4 80
2 90
2 300

output

2
3
3 1 4

input

2 100
1 787
2 788

output

0
0

input

2 100
2 42
2 58

output

2
2
1 2

Note

In the first example, you should solve problems 3, 1, and 4. In this case you'll spend 80 + 100 + 90 = 270 milliseconds, falling within the length of the exam, 300 milliseconds (and even leaving yourself 30 milliseconds to have a rest). Problems 3 and 1 will bring you a point each, while problem 4 won't. You'll score two points.

In the second example, the length of the exam is catastrophically not enough to solve even a single problem.

In the third example, you have just enough time to solve both problems in 42 + 58 = 100 milliseconds and hand your solutions to the teacher with a smile.

題目大意：n個問題，總時間為T，第i個問題有一個ai值和完成需要的時間ti，如果完成的總題數為m，則滿足ai>=m的題目得1分，現在要求一個題集，使得總得分最高

題目分析：比較明顯的二分題，因為T是限制點，按ti從小到大排序，二分答案即可

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#define ll long long 
using namespace std;
int const MAX = 2e5 + 5;
int n, T;

struct DATA {
    int a, t, id;
}d[MAX];

bool cmp(DATA d1, DATA d2) {
    return d1.t < d2.t; 
}

bool judge(int x) {
    int cnt = 0, sumt = 0;
    for (int i = 0; i < n && cnt < x; i++) {
        if (d[i].a >= x) {
            cnt ++;
            sumt += d[i].t;
        }   
    }
    //printf("cnt = %d sumt = %d\n", cnt, sumt);
    return (cnt == x && sumt <= T);
}

int main() {
    scanf("%d %d", &n, &T);
    for (int i = 0; i < n; i++) {
        scanf("%d %d", &d[i].a, &d[i].t);
        d[i].id = i + 1;
    }
    sort(d, d + n, cmp);
    int l = 0, r = n, mid, num = 0;
    while (l <= r) {
        mid = (l + r) >> 1;
        //printf("mid = %d\n", mid);
        if (judge(mid)) {
            num = mid;
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    printf("%d\n%d\n", num, num);
    int cnt = 0;
    for (int i = 0; i < n && cnt < num; i++) {
        if (d[i].a >= num) {
            cnt ++;
            if (cnt < num) {
                printf("%d ", d[i].id);
            } else {
                printf("%d", d[i].id);
            }
        }
    }
    printf("\n");
}

待補題