基本概念

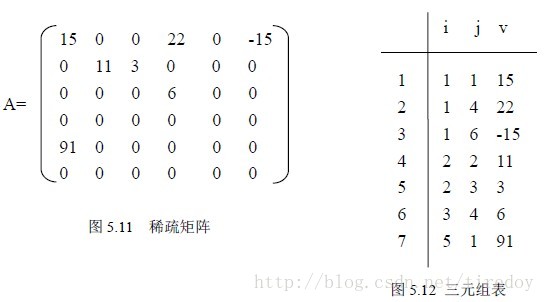
在學習線性代數的時候，經常用到矩陣。在C語言中，表示矩陣的最直觀形式就是二維陣列。然而在實際應用中，很多高階矩陣中的非零元素非常少，這個時候如果繼續使用二維陣列儲存，那麼就會浪費很多儲存空間。

在資料結構中，我們用三元組儲存稀疏矩陣。三元組定義為(i,v,j)，這三個值一次表示矩陣的行、列、值。

有了基本的概念之後，就可以定義資料結構了

定義一個結構體，來表示三元組的基本屬性

typedef struct
{
	int row, col;
	int e;
}Triple;

然後再定義一個儲存容器，用來存放三元組的

為了簡單起見，我們用陣列來實現，並定義最大儲存單元MAXSIZE為100

typedef struct
{
	Triple data[MAXSIZE];
	Int m,n,len;
}TSMatrix;
//(TSMatrix表示 Triple Sparse Matrix)

實現矩陣的轉置
         實現用三元組表示的矩陣的轉置，可以直接把行列互換，然後再執行按行序為主的排序過程。為了避免重新排序引起的元素移動，可以採用列序遞增轉置法。

         具體做法，就是遍歷列的下表值，從列數低的值到列數高的值，依次新增到快取三元組中。很顯然，這是一個雙重for迴圈結構，內層迴圈實現遍歷整個表，尋找合適的列。外層迴圈，則記錄要尋找的列數。

//實現轉置 
void TransposeTSMatrix(TSMatrix A, TSMatrix* B)
{
	int i,j,k;
	B->m = A.n;
	B->n = A.m;
	B->len = A.len;
	j=0;
	
	for( k=0; k<A.len; ++k)
	{
		for( i=0; i<A.len; ++i)
		{
			if(A.data[i].col == k)
			{
				B->data[j].row = A.data[i].col;
				B->data[j].col = A.data[i].row;
				B->data[j].e = A.data[i].e;
				++j;
			}
		}
	}
	
}
 

完整程式碼

#include <stdio.h>
#define MAXSIZE 100
//三元組的定義 
typedef struct
{
	int row, col;//表示行列 
	int e;		//表示值 
}Triple;

//三元組容器的定義 
typedef struct
{
	Triple data[MAXSIZE];
	int m,n,len;
}TSMatrix;

//實現轉置 
void TransposeTSMatrix(TSMatrix A, TSMatrix* B)
{
	int i,j,k;
	B->m = A.n;
	B->n = A.m;
	B->len = A.len;
	j=0;
	
	for( k=0; k<A.len; ++k)
	{
		for( i=0; i<A.len; ++i)
		{
			if(A.data[i].col == k)
			{
				B->data[j].row = A.data[i].col;
				B->data[j].col = A.data[i].row;
				B->data[j].e = A.data[i].e;
				++j;
			}
		}
	}
	
}

//測試驅動函式 
int main()
{
	//將輸入重定向到根目錄下的data.txt 
	freopen("data.txt", "r", stdin);
	TSMatrix A,B;
	int i,j,e; 
	int k=0;
	printf("請輸入三元組：");
	while(scanf("%d%d%d", &i, &j, &e)!=EOF)
	{
		A.data[k].row = i-1;
		A.data[k].col = j-1;
		A.data[k].e = e;
		A.len = ++k;
	}
	printf("\n原始三元組為:\n");
	for(i=0; i<A.len; ++i )
	{
		printf("%3d%3d%3d\n", A.data[i].row+1, A.data[i].col+1, A.data[i].e);
	}
	
	printf("\n轉置後:\n");
	TransposeTSMatrix(A, &B);
	for(i=0; i<B.len; ++i )
	{
		printf("%3d%3d%3d\n", B.data[i].row+1, B.data[i].col+1, B.data[i].e);
	}
	return 0;
}
 

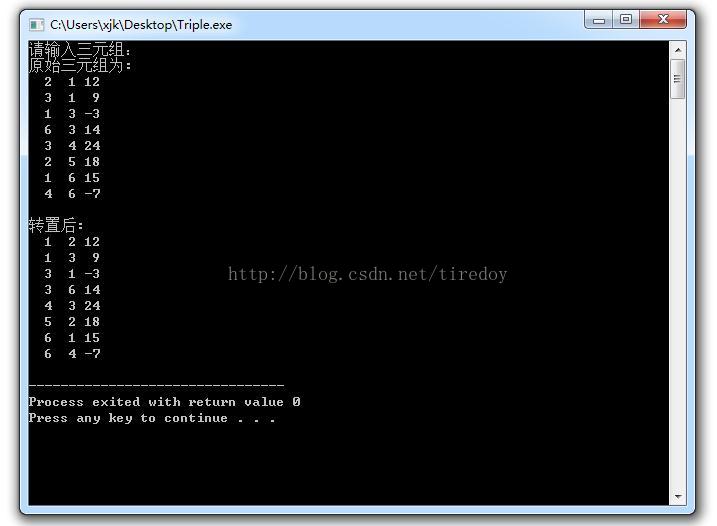
程式截圖