https://baike.baidu.com/item/%E5%90%91%E9%87%8F/1396519?fr=aladdin

1.標量和向量

    2（1,2,3) = (2,4,6) 

    (2,4,6)/2=（1,2,3)  

2.向量和向量的加減

三角形定則解決向量加減的方法：將各個向量依次首尾順次相接，結果為第一個向量的起點指向最後一個向量的終點。 平行四邊形定則解決向量加法的方法：將兩個向量平移至公共起點，以向量的兩條邊作平行四邊形， 向量的加法 結果為公共起點的對角線。 平行四邊形定則解決向量減法的方法：將兩個向量平移至公共起點，以向量的兩條邊作平行四邊形，結果由減向量的終點指向被減向量的終點。 （平行四邊形定則只適用於兩個非零非共線向量的加減。） 座標系解向量加減法： 在直角座標系裡面,定義原點為向量的起點.兩個向量和與差的座標分別等於這兩個向量相應座標的和與差若向量的表示為(x,y)形式, A(X1,Y1) B(X2,Y2)，則A+B=（X1+X2，Y1+Y2），A-B=（X2-X1，Y2-Y1） 簡單地講：向量的加減就是向量對應分量的加減。類似於物理的正交分解。

  （1,2,3)  +(2,4,6)  = （3,6,9）

  （3,6,9）-(2,4,6)=（1,2,3) 

   A向量-B向量 = 由B指向A 的向量 

   A 點-B點= B點指向A點的向量            

想得到人指向相機的向量  = 相機位置- 人位置 （假設人為原點）

 void Start () {        player = GameObject.FindGameObjectWithTag(GameTag.player).transform;  offset = transform.position - player.position;    }

3.向量模    Vector3.magnitude

空間向量(x,y,z)，其中x,y,z分別是三軸上的座標，模長是：   立方體的體對角線長度

4.向量點乘

代數定義

設二維空間內有兩個向量    和    ，定義它們的數量積（又叫內積、點積）為以下實數： 更一般地，n維向量的內積定義如下：

幾何定義

設二維空間內有兩個向量    和    ，它們的夾角為    ，則內積定義為以下實數：[2] 該定義只對二維和三維空間有效。 這個運算可以簡單地理解為：在點積運算中，第一個向量投影到第二個向量上（這裡，向量的順序是不重要的，點積運算是可交換的），然後通過除以它們的標量長度來“標準化”。這樣，這個分數一定是小於等於1的，可以簡單地轉化成一個角度值。

點乘又叫向量的內積、數量積，是一個向量和它在另一個向量上的投影的長度的乘積；是標量。 
點乘反映著兩個向量的“相似度”，兩個向量越“相似”，它們的點乘越大。

dot(a,b)              a * b = |a| * |b| * cosθ 

    cosθ 的值 在 0-90度    a * b = |a| * |b| * cosθ  >0  

                                                        90度     a * b = |a| * |b| * cosθ  = 0

                                                  90-180度    a * b = |a| * |b| * cosθ < 0

                                          

 1.圖形學中表示光照強度

   當a 和e 都是單位向量時 a * b = |a| * |b| * cosθ  =   cosθ 

    float3 normalDir =  normalize(mul(v.normal,_World2Object));   //模型空間到世界空間  方向轉換  矩陣--_World2object

   fixed3 lightDir = normalize(_WorldSpaceLightPos0.xyz) ; // ，平行光，對頂點來說，光位置就是光方向

   // LightColor0.rgb   平行光顏色   _Diffuse.rgb  自定義顏色  ， 標準化的向量點積求出 cosθ  ,

    //使用 cosθ 表示光強，和法線垂直最亮，平行最暗

   float3 diffuse = _LightColor0.rgb*max(dot(normalDir,lightDir),0)*_Diffuse.rgb; 

2.位置判斷

float c = Vector3.Dot (a, b); 

 通過點積的計算我們可以簡單粗略的判斷當前物體是否朝向另外一個物體: 只需要計算當前物體的transform.forward向量與 (otherObj.transform.position – transform.position)的點積即可， 大於0則面對，否則則背對著。

 或者，通過點積後的大小判斷向量夾角是銳角，鈍角，還是直角

5.向量叉乘

a ∧ b = |a| * |b| * sinθ 

(a,b,c)×(x,y,z)=(bz-cy,cx-az,ay-bx)

向量積被定義為： 
模長：（在這裡θ表示兩向量之間的夾角(共起點的前提下)（0° ≤ θ ≤ 180°），它位於這兩個向量所定義的平面上。） 
方向：a向量與b向量的向量積的方向與這兩個向量所在平面垂直，且遵守右手定則。（一個簡單的確定滿足“右手定則”的結果向量的方向的方法是這樣的：若座標系是滿足右手定則的，當右手的四指從a以不超過180度的轉角轉向b時，豎起的大拇指指向是c的方向。c = a ∧ b） 

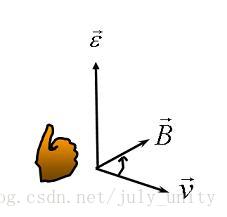
  叉積的定義：c =a x b 其中a,b,c均為向量。即兩個向量的叉積得到的還是向量！  性質1：c⊥a，c⊥b，即向量c垂直與向量a,b所在的平面。  性質2：模長|c|=|a||b|sin<a,b>  性質3：滿足右手法則。從這點我們有axb ≠ bxa，而axb = – bxa。所以我們可以使用叉積的正負值來判斷向量a，b的相對位置，即向量b是處於向量a的順時針方向還是逆時針方向。

在力學裡,用叉積表示一個力對 一個定點的矩M=r×F,當F與向徑r不垂直時,二者有個夾角θ,那麼︱M︱=︱r︱︱F︱sinθ,力 矩M是向量，總之，外積就是，產生一個新向量，其方向垂直於由向量AB，向量CD確定的平面，其方向由右手定則確定。

1 .計算出兩個向量的夾角。  下面是示例程式碼:

using UnityEngine;  

using System.Collections;  

publicclass MainScript : MonoBehaviour  

{  //向量a

private Vector3 a;  

//向量b

private Vector3 b;  

void Start ()  

      {  

//向量的初始化

              a = new Vector3 (1, 2, 1);  

               b = new Vector3 (5, 6, 0);  

        }  

void OnGUI ()  

       {  

//點積的返回值

float c = Vector3.Dot (a, b);  

//向量a,b的夾角,得到的值為弧度，我們將其轉換為角度，便於檢視！

float angle = Mathf.Acos (Vector3.Dot (a.normalized, b.normalized)) * Mathf.Rad2Deg;  

             GUILayout.Label ("向量a，b的點積為：" + c);  

               GUILayout.Label ("向量a，b的夾角為：" + angle);  

//叉積的返回值

              Vector3 e = Vector3.Cross (a, b);  

                Vector3 d = Vector3.Cross (b, a);  

//向量a,b的夾角,得到的值為弧度，我們將其轉換為角度，便於檢視！

               angle = Mathf.Asin (Vector3.Distance (Vector3.zero, Vector3.Cross (a.normalized, b.normalized))) * Mathf.Rad2Deg;  

               GUILayout.Label ("向量axb為：" + e);  

              GUILayout.Label ("向量bxa為：" + d);  

                GUILayout.Label ("向量a，b的夾角為：" + angle);  

        }  

}  

  上面的示例中，我們定義了兩個向量a和b。分別求出了他們的點積和叉積，並通過點積和叉積來反過來計算他們的夾角。

  這裡要說明的是:     通過叉積計算度數是通過公式|c|=|a||b|sin<a,b>來逆向求值。|c| 其實就是叉積的模，換句話說，也代表著Vector3.Distance (Vector3.zero, Vector3.Cross (a.normalized, b.normalized))的值。

   2.用來判斷一個向量在另一個向量的左側還是右側，通過叉乘後向量的方向判斷向量的位置

float GetAngularSpeed()    {// 求出夾角        float angle = Vector3.Angle(transform.forward, nav.desiredVelocity);

// 求弧度
        float result = angle * Mathf.Deg2Rad;
   // 期望速度在機器人左側則弧度為負，否則為正
 Vector3 normal = Vector3.Cross(transform.forward, nav.desiredVelocity);
    if (normal.y < 0)        {
            // 說明在左側 (A 為Z方向時，B在A的逆時針180度內，此時點積小於0，方向向下，y值小於0 )
            result *= -1;
        }//if (nav.desiredVelocity == Vector3.zero)//{//    result = 0;//}        return result;    }

6 . 向量求夾角------Vector3.Angle(a, b) 

   返回的角度是倆個向量中小於180度的角度，是不分左右的，沒有負數

  1.HTC中把touchPad分為N等分，可以擴充套件為N個功能鍵

  // 如下，控制遊玩區前後左右移動    x 形區域，實現控制

// Update is called once per frame

void Update () {

  if (device.GetPress(SteamVR_Controller.ButtonMask.Touchpad))

        {

Vector2 pos = device.GetAxis();

GameObject cameraRig = transform.parent.gameObject;

            if (Vector2.Angle(Vector2.up, pos) < 45)

            {

                cameraRig.transform.Translate(Vector3.forward *Time.deltaTime);

            }

            else if(Vector2.Angle(Vector2.right, pos) < 45)

            {

Debug.Log("右");

                cameraRig.transform.Translate(Vector3.right *Time.deltaTime);

            }

            else if (Vector2.Angle(Vector2.left, pos) < 45)

            {

Debug.Log("左");

                cameraRig.transform.Translate(Vector3.left *Time.deltaTime);

            }

            else if(Vector2.Angle(Vector2.down, pos) < 45)

            {

Debug.Log("下");

                cameraRig.transform.Translate(Vector3.back *Time.deltaTime);

            }

        }

}

2.設定怪物視野

   public float sightAngle = 110;// 獲取玩家    private Transform player;// 能否看到玩家    public bool canSeePlayer = false;

 bool CheckSight()    {        Vector3 dir = player.position - transform.position;        if (Vector3.Angle(transform.forward, dir) < sightAngle / 2)        {            Ray ray = new Ray(transform.position + Vector3.up * 1.7f, dir);            RaycastHit hit;// 中間不能有障礙物            if (Physics.Raycast(ray, out hit))            {                if (hit.collider.tag == GameTag.player)                {                    canSeePlayer = true; return true;                }            }        }  return false;    }

7.向量投影 Vector3 project

a點乘b向量=a向量的模乘以b向量的模乘以cosa ，

b向量的模cosa 叫做 a向量在b向量方向上的投影，等同於點積一個單位化向量

Vector3 project = Vector3.Project(nav.desiredVelocity, transform.forward);  

空間倆點間的距離

Vector3.Distance(a,b) 等同於(a-b).magnitude 。

• 點時，表示倆點距離，即倆個相對於原點的向量，求距離

var other : Transform;
if (other) {
	var dist = Vector3.Distance(other.position, transform.position);
	print ("Distance to other: " + dist);
}

bool CheckVoice()    {
// 獲取e玩家的腳步聲
        if (player.GetComponent<AudioSource>().isPlaying)
        {
// 定義一條導航路徑
 NavMeshPath path = new NavMeshPath();// 判斷在當前的導航烘焙下，敵人是否能到達腳步聲的位置
            if (nav.CalculatePath(player.position, path))            {// 定義一個拐點陣列，用來存放這條路徑上所有拐點位置資訊(不包含起點和終點)                Vector3[] corners = path.corners;
                Vector3[] pathPoints = new Vector3[corners.Length + 2];
 pathPoints[0] = transform.position;
                pathPoints[pathPoints.Length - 1] = player.position;
                for (int i = 0; i < corners.Length; i++)
                {
                    pathPoints[i + 1] = corners[i];
                }
// 此路徑的總距離
                float pathDistance = 0;
                for (int i = 0; i < pathPoints.Length - 1; i++)
                {
  pathDistance += Vector3.Distance(pathPoints[i], pathPoints[i + 1]);    // 空間倆點間的距離
                }
// 若總距離小於觸發器的半徑，則代表聽到了聲音
                if (pathDistance < GetComponent<SphereCollider>().radius)
                {
                    return true;
                }
            }
        }
        return false;
    }