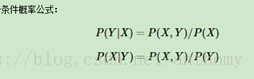《機器學習實戰》NaiveBayes演算法原理及實現
一、問題描述
鳶尾花(IRIS)有很多種,但又因為特徵很是相近,不好區分,通過大量資料歸納的特徵,我們通過花萼長度(Sepal.Length),花萼寬度(Sepal.Width),花瓣長度(Petal.Length),花瓣寬度(Petal.Width),4個屬性預測鳶尾花卉屬於(Setosa,Versicolour,Virginica)三個種類中的哪一類,從而更加有效地進行區分。
二、演算法原理
樸素貝葉斯最核心的部分是貝葉斯法則,而貝葉斯法則的基石是條件概率。
Bayesianinferenc(貝葉斯推斷):根據一個已發生事件的概率,計算另一個事件的發生概率,在可以選擇分類中概率最大的就是該事件的分類。
三、資料描述及視覺化
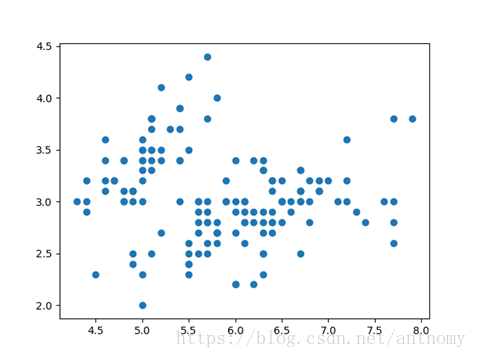
橫座標:花萼長度(Sepal.Length)
縱座標:花萼寬度(Sepal.Width)
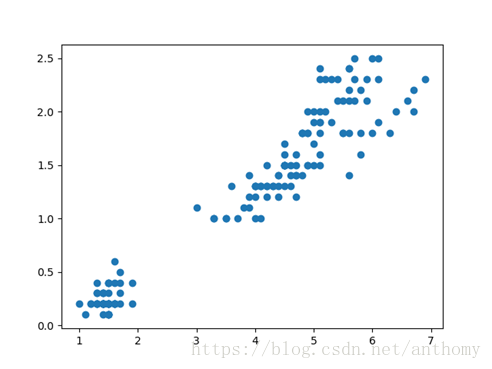
橫座標:花瓣長度(Petal.Length)
縱座標:花瓣寬度(Petal.Width)
四、演算法的程式實現
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = ones(numWords); p1Num = ones(numWords) #change to ones()
p0Denom = 2.0; p1Denom = 2.0 #change to 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num/p1Denom) #change to log()
p0Vect = log(p0Num/p0Denom) #change to log()
return p0Vect,p1Vect,pAbusive
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):p1 = sum(vec2Classify * p1Vec) + log(pClass1) #element-wise mult
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
五、測試結果及分析
選取50%、60%、70%、80%的資料做測試集,繪製正確率折線圖,對比1、2兩種演算法的正確率
測試資料比例 正確率 錯誤率
10% 1.000000 0
20% 1.000000 0
30% 0.936170 0.063830
40% 0.966102 0.033898
50% 0.957447 0.042553
60% 0.920000 0.080000
70% 0.950000 0.065217
80% 0.933333 0.066667
90% 0.330827 0.669173
在測試資料量到80%之前演算法分類出錯的概率都非常低,80%之後錯誤率有明顯提高。
六、總結與體會
模型所需估計的引數很少,對缺失資料不太敏感,演算法也比較簡單。理論上,模型與其他分類方法相比具有最小的誤差率。但是實際上並非總是如此,這是因為模型假設屬性之間相互獨立,這個假設在實際應用中往往是不成立的,這給NBC模型的正確分類帶來了一定影響.
七、參考文獻
【2】Peter Harrington。《機器學習實戰》
【3】python使用matplotlib繪製柱狀圖教程
http://www.jb51.net/article/104924.htm
非常感謝閱讀!如有不足之處,請留下您的評價和問題。