積分公式

令曲線y=f(x)繞x軸旋轉，形成的旋轉體，則其體積和表面積可以計算積分而得（假設體積和表面積一定存在，積分一定存在，這裡不討論數學問題）。
體積公式為：

ZOJ3866 Cylinder Candy

ZOJ3866，一個圓柱體半徑為rmm，高度為hmm，外圍包裹著dmm厚的塗層，求其表面積和體積。這個題目要精確到10−8，推不出積分公式就不用做了。

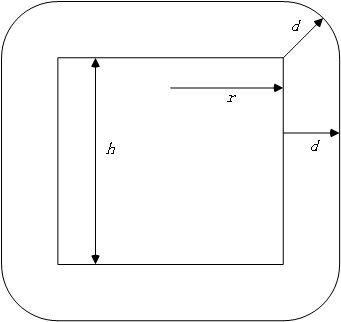
整個部分最關鍵的就是四個邊角的形狀，四個邊角合在一起恰好是一個圓環的外半側。所以關鍵就是求圓環的外半側的體積以及表面積。
曲線方程為：

然後把其他部分的圓柱體算上即可。

#include <cstdio>
#include <cmath>

double const PI = acos(-1.0);
double const DELTA = 1E-6;
double R,H,D;

double integral(){
    return (2.0*D*R*R+4.0*D*D*D/3.0+D*D*R*PI) * PI;
}

double integral2(){
    return 4.0*PI*D*D + 2.0
 
*PI*PI*R*D;
}

int main(){
    int nofkase;
    scanf("%d",&nofkase);
    while( nofkase-- ){
        scanf("%lf%lf%lf",&R,&H,&D);
        double v = integral() + PI * ( R + D ) * ( R + D ) * H;
        double s = integral2() + 2.0 * PI * ( R + D ) * H + 2.0 * PI * R * R;
        printf("%.12lf %.12lf\n",v,s);
    }
    return 0;
}

ZOJ3898 Stean

ZOJ3898同樣是旋轉體的表面積和體積。曲線為：