主成分分析與因子分析及SPSS實現
阿新 • • 發佈:2019-01-28
一、主成分分析
(1)問題提出在問題研究中,為了不遺漏和準確起見,往往會面面俱到,取得大量的指標來進行分析。比如為了研究某種疾病的影響因素,我們可能會收集患者的人口學資料、病史、體徵、化驗檢查等等數十項指標。如果將這些指標直接納入多元統計分析,不僅會使模型變得複雜不穩定,而且還有可能因為變數之間的多重共線性引起較大的誤差。有沒有一種辦法能對資訊進行濃縮,減少變數的個數,同時消除多重共線性?這時,主成分分析隆重登場。(2)主成分分析的原理主成分分析的本質是座標的旋轉變換,將原始的n個變數進行重新的線性組合,生成n個新的變數,他們之間互不相關,稱為n個“成分”。同時按照方差最大化的原則,保證第一個成分的方差最大,然後依次遞減。這n個成分是按照方差從大到小排列的,其中前m個成分可能就包含了原始變數的大部分方差(及變異資訊)。那麼這m個成分就成為原始變數的“主成分”,他們包含了原始變數的大部分資訊。注意得到的主成分不是原始變數篩選後的剩餘變數,而是原始變數經過重新組合後的“綜合變數”。我們以最簡單的二維資料來直觀的解釋主成分分析的原理。假設現在有兩個變數X1、X2,在座標上畫出散點圖如下: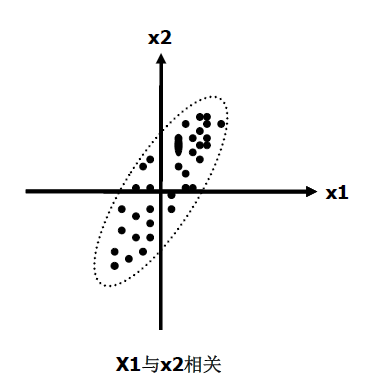
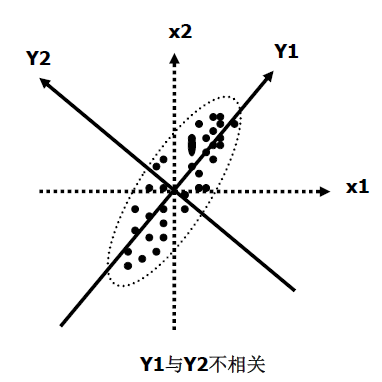 根據座標變化的原理,我們可以算出:Y1 = sqrt(2)/2 * X1 + sqrt(2)/2 * X2Y2 = sqrt(2)/2 * X1 – sqrt(2)/2 * X2其中sqrt(x)為x的平方根。通過對X1、X2的重新進行線性組合,得到了兩個新的變數Y1、Y2。此時,Y1、Y2變得不再相關,而且Y1方向變異(方差)較大,Y2方向的變異(方差)較小,這時我們可以提取Y1作為X1、X2的主成分,參與後續的統計分析,因為它攜帶了原始變數的大部分資訊。至此我們解決了兩個問題:降維和消除共線性。對於二維以上的資料,就不能用上面的幾何圖形直觀的表示了,只能通過矩陣變換求解,但是本質思想是一樣的。
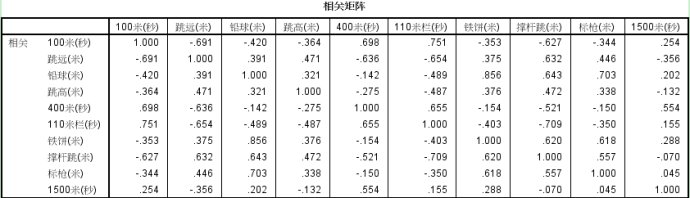
根據座標變化的原理,我們可以算出:Y1 = sqrt(2)/2 * X1 + sqrt(2)/2 * X2Y2 = sqrt(2)/2 * X1 – sqrt(2)/2 * X2其中sqrt(x)為x的平方根。通過對X1、X2的重新進行線性組合,得到了兩個新的變數Y1、Y2。此時,Y1、Y2變得不再相關,而且Y1方向變異(方差)較大,Y2方向的變異(方差)較小,這時我們可以提取Y1作為X1、X2的主成分,參與後續的統計分析,因為它攜帶了原始變數的大部分資訊。至此我們解決了兩個問題:降維和消除共線性。對於二維以上的資料,就不能用上面的幾何圖形直觀的表示了,只能通過矩陣變換求解,但是本質思想是一樣的。二、因子分析(一)原理和方法:因子分析是主成分分析的擴充套件。在主成分分析過程中,新變數是原始變數的線性組合,即將多個原始變數經過線性(座標)變換得到新的變數。因子分析中,是對原始變數間的內在相關結構進行分組,相關性強的分在一組,組間相關性較弱,這樣各組變數代表一個基本要素(公共因子)。通過原始變數之間的複雜關係對原始變數進行分解,得到公共因子和特殊因子。將原始變量表示成公共因子的線性組合。其中公共因子是所有原始變數中所共同具有的特徵,而特殊因子則是原始變數所特有的部分。因子分析強調對新變數(因子)的實際意義的解釋。舉個例子:比如在市場調查中我們收集了食品的五項指標(x1-x5):味道、價格、風味、是否快餐、能量,經過因子分析,我們發現了:x1 = 0.02 * z1 + 0.99 * z2 + e1x2 = 0.94 * z1 – 0.01 * z2 + e2x3 = 0.13* z1 + 0.98 * z2 + e3x4 = 0.84 * z1 + 0.42 * z2 + e4x5 = 0.97 * z1 – 0.02 * z2 + e1(以上的數字代表實際為變數間的相關係數,值越大,相關性越大)第一個公因子z1主要與價格、是否快餐、能量有關,代表“價格與營養”第二個公因子z2主要與味道、風味有關,代表“口味”e1-5是特殊因子,是公因子中無法解釋的,在分析中一般略去。同時,我們也可以將公因子z1、z2表示成原始變數的線性組合,用於後續分析。(二)使用條件:(1)樣本量足夠大。通常要求樣本量是變數數目的5倍以上,且大於100例。(2)原始變數之間具有相關性。如果變數之間彼此獨立,無法使用因子分析。在SPSS中可用KMO檢驗和Bartlett球形檢驗來判斷。(3)生成的公因子要有實際的意義,必要時可通過因子旋轉(座標變化)來達到。三、主成分分析和因子分析的聯絡與區別聯絡:兩者都是降維和資訊濃縮的方法。生成的新變數均代表了原始變數的大部分資訊且互相獨立,都可以用於後續的迴歸分析、判別分析、聚類分析等等。區別:(1)主成分分析是按照方差最大化的方法生成的新變數,強調新變數貢獻了多大比例的方差,不關心新變數是否有明確的實際意義。(2)因子分析著重要求新變數具有實際的意義,能解釋原始變數間的內在結構。SPSS沒有提供單獨的主成分分析方法,而是混在因子分析當中,下面通過一個例子來討論主成分分析與因子分析的實現方法及相關問題。一、問題提出男子十項全能比賽包含100米跑、跳遠、跳高、撐杆跳、鉛球、鐵餅、標槍、400米跑、1500米跑、110米跨欄十個專案,總分為各個專案得分之和。為了分析十項全能主要考察哪些方面的能力,以便有針對性的進行訓練,研究者收集了134個頂級運動員的十項全能成績單,將通過因子分析來達到分析目的。二、分析過程變數檢視:
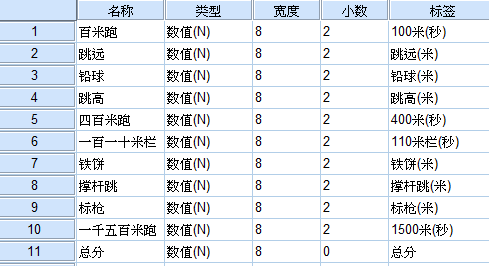
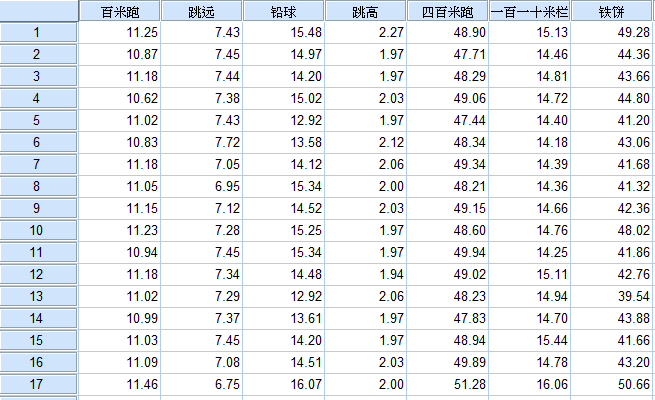 選單選擇(分析->降維->因子分析):
選單選擇(分析->降維->因子分析):
 點選”描述“按鈕,開啟對話方塊,選中”係數“和”KMO和Bartlett球形度檢驗“:
點選”描述“按鈕,開啟對話方塊,選中”係數“和”KMO和Bartlett球形度檢驗“:
 上圖有兩個指標:第一個是KMO值,一般大於0.7就說明不了之間有相關性了。第二個是Bartlett球形度檢驗,P值<0.001。綜合兩個指標,說明變數之間存在相關性,可以進行因子分析。否則,不能進行因子分析。(2)提取主成分和公因子接下來輸出主成分結果:
上圖有兩個指標:第一個是KMO值,一般大於0.7就說明不了之間有相關性了。第二個是Bartlett球形度檢驗,P值<0.001。綜合兩個指標,說明變數之間存在相關性,可以進行因子分析。否則,不能進行因子分析。(2)提取主成分和公因子接下來輸出主成分結果: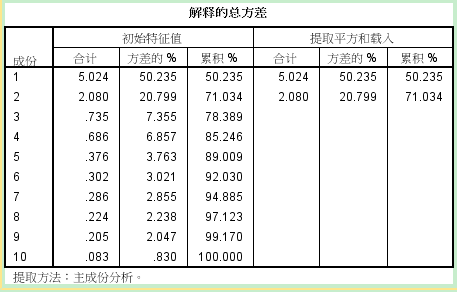
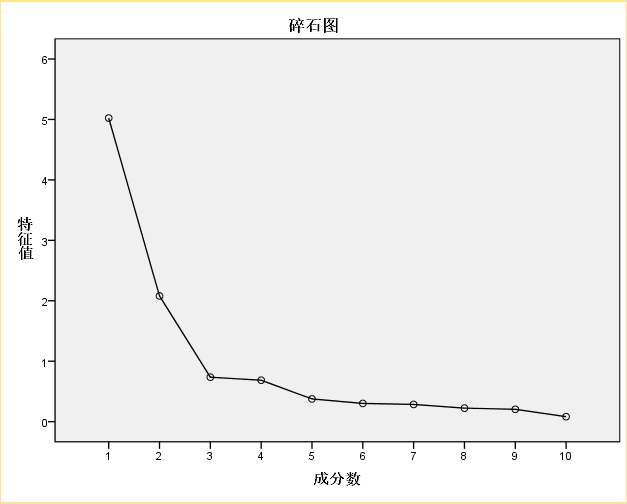 碎石圖來源於地質學的概念。在岩層斜坡下方往往有很多小的碎石,其地質學意義不大。碎石圖以特徵值為縱軸,成分為橫軸。前面陡峭的部分特徵值大,包含的資訊多,後面平坦的部分特徵值小,包含的資訊也小。由圖直觀的看出,成分1和2包含了大部分資訊,從3開始就進入平臺了。接下來,輸出提取的成分矩陣:
碎石圖來源於地質學的概念。在岩層斜坡下方往往有很多小的碎石,其地質學意義不大。碎石圖以特徵值為縱軸,成分為橫軸。前面陡峭的部分特徵值大,包含的資訊多,後面平坦的部分特徵值小,包含的資訊也小。由圖直觀的看出,成分1和2包含了大部分資訊,從3開始就進入平臺了。接下來,輸出提取的成分矩陣: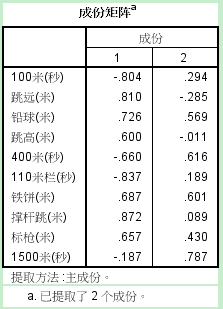
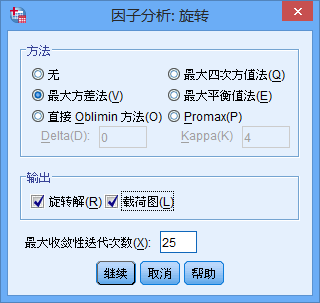
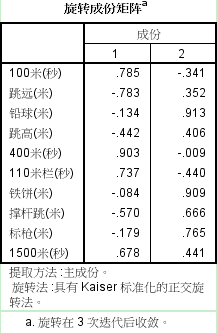 這是選擇後的成分矩陣。經過旋轉,可以看出:公因子1得分越高,所有的跑步和跨欄成績越差,而跳遠、撐杆跳等需要助跑類專案的成績也越差,所以公因子1代表的是奔跑能力的反向指標,可稱為“奔跑能力”。公因子2與鐵餅和鉛球的正相關性很高,與標槍、撐杆跳等需要上肢力量的專案也正相關,所以該因子可以成為“上肢力量”。經過旋轉,可以看出公因子有了更合理的解釋。(四)結果的儲存在最後,我們還要將公因子儲存下來供後續使用。點選“得分”按鈕,開啟對話方塊,選中“儲存為變數”,方法採用預設的“迴歸”方法,同時選中“顯示因子得分系數矩陣”。
這是選擇後的成分矩陣。經過旋轉,可以看出:公因子1得分越高,所有的跑步和跨欄成績越差,而跳遠、撐杆跳等需要助跑類專案的成績也越差,所以公因子1代表的是奔跑能力的反向指標,可稱為“奔跑能力”。公因子2與鐵餅和鉛球的正相關性很高,與標槍、撐杆跳等需要上肢力量的專案也正相關,所以該因子可以成為“上肢力量”。經過旋轉,可以看出公因子有了更合理的解釋。(四)結果的儲存在最後,我們還要將公因子儲存下來供後續使用。點選“得分”按鈕,開啟對話方塊,選中“儲存為變數”,方法採用預設的“迴歸”方法,同時選中“顯示因子得分系數矩陣”。
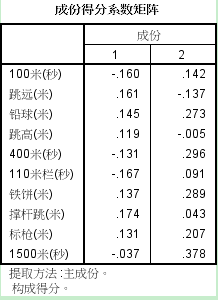
由上圖,我們可以寫出公因子的表示式(用F1、F2代表兩個公因子,Z1~Z10分別代表原始變數):
F1 = -0.16*Z1+0.161*Z2+0.145*Z3+0.199*Z4-0.131*Z5-0.167*Z6+0.137*Z7+0.174*Z8+0.131*Z9-0.037*Z10F2同理,略去。注意,這裡的變數Z1~Z10,F1、F2不再是原始變數,而是標準正態變換後的變數。