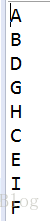前幾天參加了阿里暑期實習的內推面試，發現自己的資料結構演算法基礎特別薄弱，比如其中一個問題是中序遍歷的遞迴與非遞迴演算法，我平時看資料結構只知道遞迴演算法，非遞迴的演算法直接被問懵逼了，在思考了幾十秒之後想出了用陣列存放每次遍歷節點的父節點，然後用for迴圈遍歷，雖然可以實現，但是我覺得面試官聽到之後估計在吐血，還有HashMap底層自己明明知道用的是散列表，在緊張之下我竟然說是陣列，面完之後被舍友吐槽，所以下定決心好好把演算法基礎打紮實了，雖然面試的不怎麼樣，但是能夠知道自己的資料結構基礎太薄弱了還是有收穫的。

     這篇博文主要是研究前序遍歷的遞迴與非遞迴演算法，後面還會慢慢有中序和後序的遞迴與非遞迴演算法。

之前看的關於資料結構的書籍，在二叉樹那一章的前序遍歷主要講的是遞迴演算法，在這裡也複習一下

先初始化二叉樹

public TreeNode initTree(){
		TreeNode G = new TreeNode("G", null, null);
		TreeNode H = new TreeNode("H", null, null);
		TreeNode D = new TreeNode("D", G, H);
		TreeNode B = new TreeNode("B", D, null);
		TreeNode I = new TreeNode("I", null, null);
		TreeNode E = new TreeNode("E", null, I);
		TreeNode F = new TreeNode("F", null, null);
		TreeNode C = new TreeNode("C", E, F);
		TreeNode A = new TreeNode("A", B, C);
		return A;
	}
 

再進行二叉樹的前序遞迴遍歷

public void preOrderTraverse(TreeNode T){  //前序遍歷遞迴演算法
		if(T==null){
			return;
		}
		
		System.out.println(T.data);     //對節點進行處理，這裡用輸出代替處理
		preOrderTraverse(T.lchild);     
		preOrderTraverse(T.rchild);
		
	}

以上是前序遞迴遍歷，程式碼簡潔，如果對遞迴演算法理解透徹的話，前序遞迴遍歷很好理解，這裡就不做過多闡述。雖然遞迴遍歷簡單和好理解，但是面對海量資料的時候，由於遞迴演算法需要建立很多物件，需要佔用大量記憶體，使得空間複雜度極大，也容易造成堆疊的溢位，因此遞迴演算法面對海量資料時還是有非常致命的缺陷，下面探究一下前序遍歷的非遞迴演算法。

當用非遞迴遍歷時，我們不能夠像遞迴遍歷那樣呼叫自己的方法來訪問子節點，那怎麼辦呢？第一個出現在腦海中的想法便是用迴圈是遍歷每一個節點，但是當遍歷到葉子節點的時候我們需要回到前面遍歷之前沒有遍歷到的右節點，這可怎麼辦？當初在面試的時候因為就給了幾十秒的時間有點緊張，所以想出了用陣列儲存每次遍歷後的節點的父節點，但其實二叉樹的前序遍歷有個特點就是遍歷到左葉子節點的時候需要回頭再去遍歷之前未遍歷到的右節點，這個特點剛好和棧的先進後出的特點很相符，所以應該改用棧來儲存未遍歷到的右節點

程式碼如下

public void preOrderWithoutRecursion(TreeNode T){ //前序遍歷非遞迴演算法
		
		TreeNode p;
		Stack<TreeNode> stack = new Stack<TreeNode>();
		stack.push(T);             //先將根節點壓進棧中
		while(T!=null&&!stack.empty()){
			p = stack.pop();        //彈出棧頂的節點賦給p
			System.out.println(p.data);  //用輸出來代替對節點的處理
			if(p.rchild!=null){           
				stack.push(p.rchild);      //如果彈出節點的右孩子不為空則壓入棧
			}	                        //注意，這裡的重點是一定要先將右孩子壓入棧，再將左孩子壓入
			if(p.lchild!=null){
				stack.push(p.lchild);     //如果彈出節點的左孩子不為空則壓入棧
			}		
		}	
		
	}

與遞迴的演算法結果一樣

雖然非遞迴演算法的程式碼量比遞迴稍多了一點，但是對於海量資料來說非遞迴演算法的空間複雜度遠低於遞迴演算法，也不容易造成堆疊溢位。