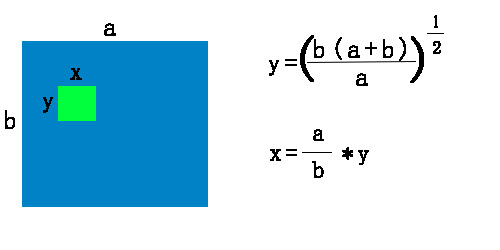影象的自適應二值化

阿新 • • 發佈：2019-01-28

機器視覺分為三個階段 : 影象轉化、影象分析、影象理解。若要將一幅影象轉化為方便分析理解的格式，有一個很關鍵的過程就是“影象二值化”。一幅影象能否分析理解的準確很大程度上來說取決於二值化效果的好壞。然而目前國際上還沒有任何二值化標準的演算法，也沒相關的確定性數學模型建立。這裡我大致介紹我這幾天研究的鄙見。

在二值化前有一個很重要的步驟是“影象灰度化”，原理就是將原RGB影象的三維矩陣進行f(x) = R*0.3+G*0.51+B*0.11運算得到一個二維矩陣（個人認為一個維度承載著一類資訊，一維影象能夠傳達一根線的資訊，二維影象能傳達一幅圖片資訊，而這第三維便是顏色資訊，所以三維降到二維影象自然失去了顏色），至於函式的由來不得而知，還望有專業人士指教。

著名的lenna ==灰度化==》》這裡寫圖片描述

二值化演算法是取一個閾值，將大於閾值的畫素點取值1即顯示白色，而小於閾值的畫素點自然賦值為0即顯示為黑色。所以這個閾值確定的好壞直接影響到效果。最簡單的閾值取定便是取整幅圖畫的均值mean了:

這裡寫圖片描述 ==均值二值化==》

上述效果感覺還不錯，但是對於某些圖效果就沒這麼樂觀了，比如

這裡寫圖片描述 ==均值二值化==》

這類受到光線陰影而影響到降低均值的圖片，部分陰影區域的畫素點會比均值低，所以可能會在陰影區域出現死黑的區域，所以單一的取均值來二值化是不夠完美的。

讓我們來思考下原因：這個整幅影象的均值可以認為是整幅影象資訊的一個綜合資料，將畫素點與均值比對在一定程度上可以理解為該畫素點與整幅影象的關係。但是一個畫素點真的會與整幅影象的所有畫素點都有關係麼？答案當然是否定的，我查閱了一些資料，有一種叫做

自適應二值化的演算法（每個畫素點比對的閾值不同的演算法總稱），他將二維矩陣合成一行，然後將每個畫素點與前面一定範圍內畫素點通過某種方法計算出來的值進行比對，這種演算法出來的影象可以說是攜帶了行方向的畫素點關係，但是在列方向上的呢？所以我加了些改進，糅合了行列方向資訊的演算法，我給他取名為“十字二值化演算法”，即每一個畫素點的閾值取它所在的行列的所有畫素點的均值mean1：
這裡寫圖片描述

做出的效果如下

十字二值化演算法

雖然效果比取全域性均值的效果要好一點點，在陰影區域已經顯露出部分字型，但是效果並不令人滿意。

仔細想想，畫素點的資訊是否與所處的行列都有關呢？很大的可能性是隻與較近的十字畫素區域有關，較遠的則很少有關了。進一步思考，陰影部分畫素點在全局面前也許是個黑點，但在其周圍附近卻可能是個白點，是否與較近的一塊矩形區域內的畫素點有關呢？我們不妨嘗試下，畫素點個數為行列畫素個數之和，矩形區域的長寬比與影象的長寬比相同，容易推出公式（我把它名為“矩陣二值化演算法”

）：

這裡寫圖片描述

括號裡的（a+b）為自己設定的小矩陣的畫素點個數，可以自行設定。我們把這麼一個小矩陣稱為顆粒，把矩陣的大小稱之為顆粒度，理所當然一幅影象，顆粒度越大則顆粒越少，反之越多。而均值二值化即可認為整幅影象為一個顆粒度。後面我們將會意識到顆粒度的大小會對影象有很大的影響。這裡預設為a+b，有如下效果：

矩陣二值化演算法，顆粒度為影象畫素的長+寬

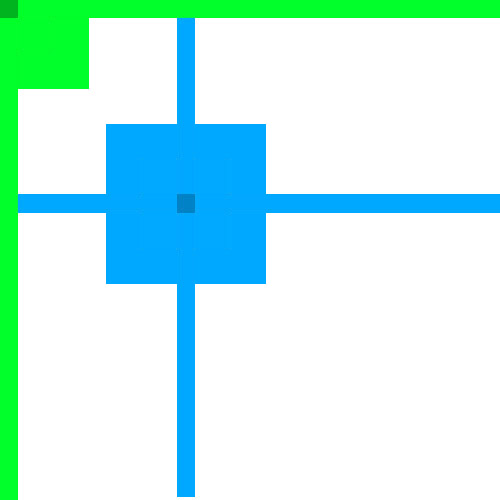
頓時眼前一亮！這是個突破！字型（細節）全部顯現出來了，可為什麼其他地方（平滑的區域）卻出現了“麻點呢”？原因是這些區域內所求畫素點附近矩陣內的所有畫素點灰度值都極度相近，這造成所求畫素點與附近畫素點灰度值的均值也極度相近，那麼會產生大約50比50的概率大於均值，所以在平滑的區域黑白機率也就一半一半了。這就上升到了一個區域性與全域性的權衡問題，要想故及全域性，則會想均值二值化那樣出現死黑區域，而想區域性計算則會出現這樣的亂點問題。那我們時候可以綜合“十字二值化演算法”和“矩陣二值化演算法”來達到全域性與區域性的最平衡呢？這也就是我當初設定矩陣顆粒度為影象長+寬的原因了，將兩者演算法綜合，演算法各自涉及的畫素點皆為長+寬個數，也是一半一半。平衡嘛！

這裡寫圖片描述

我將他命名為“十字矩陣二值化演算法”，其效果為：

十字矩陣二值化演算法

能夠開心的發現，影象效果像演算法那樣也綜合了，雖然任然有瑕疵，但至少取得了一定的成功。

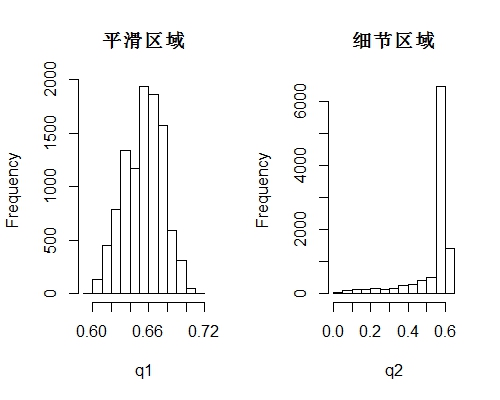
經過我一整夜的思考，我想無論我和權衡十字二值化演算法（處理平滑區域較好）和矩陣二值化演算法（處理細節完美），始終會在全域性和區域性上有問題，所以我乾脆擯棄這個權衡的思想，進而思考如何將矩陣二值化演算法平滑區域的亂點去除。也就是如何分辨細節區域和平滑區域。因此我截取了部分細節區域和平滑區域，觀察其值的直方圖

這裡寫圖片描述

可以觀察到在平滑區域，畫素點的灰度值在一個很小的區間，且呈現中間突出的分佈曲線；而在細節區域，畫素點的灰度值卻分佈在很大的一個區間，呈現出極端分佈的規律，只要我們能正確區別兩種區域便能有效處理影象。因此我在 “矩陣二值化演算法” 中，畫素點與矩陣內所有畫素點的均值比對過程中加了一個引數β，即if( a ＜mean*β）,這個引數β經過我多張照片測試後調為0.9。其效果為：

引數矩陣二值化演算法

效果終於達到了，細節得以體現，平滑區域也無半點影響。perfect！

———————————————————————————————————————————-

以下是R程式碼

binarization<-function(matrix,tar = '',rate = 0.9){
  if(length(dim(matrix)) == 3){
    matrix<-rgb_to_gray(matrix)
  }
  mat<-array(dim = dim(matrix))

  hh<-dim(matrix)[1]
  ww<-dim(matrix)[2]

  height<-sqrt(hh/ww*(hh+ww))
  width<-ww/hh*height

  for(i in 1:dim(matrix)[1]){
    for(k in 1:dim(matrix)[2]){
      h1<-i-floor(height/2)
      h2<-i+floor(height/2)
      w1<-k-floor(width/2)
      w2<-k+floor(width/2)
      if(h1<1)
        h1<-1
      if(w1<1)
        w1<-1
      if(h2>dim(matrix)[1])
        h2<-dim(matrix)[1]
      if(w2>dim(matrix)[2])
        w2<-dim(matrix)[2]
      mat[i,k]<-mean(matrix[h1:h2,w1:w2])
    }
  }

  mat[matrix<mat*rate]<-0
  mat[mat!=0]<-1

  if(tar == ''){
    return(mat)
  }else{
    writeJPEG(image = mat,target = tar)
  }
}