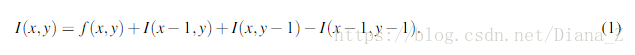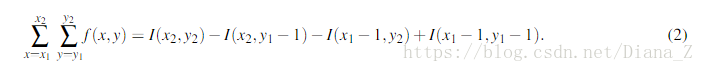論文：Adaptive Thresholding Using the Integral Image

地址：https://www.researchgate.net/publication/220494200_Adaptive_Thresholding_using_the_Integral_Image

應用：matlab二值化函式 T = adaptthresh(I)

這應該是adapthresh中的一個方法，但是不是高斯

-----------------------------------------------------------------------------------------

摘要：  影象閾值處理是許多計算機視覺和圖形應用中的常見任務。 對影象進行閾值處理的目的是將畫素分類為“暗”或“亮”。 自適應閾值處理是一種閾值處理，它考慮了照明的空間變化。 我們提出了一種使用輸入的積分影象進行實時自適應閾值處理的技術。 我們的技術是以前方法的擴充套件。 但是，我們的解決方案對影象中的照明變化更加穩健。 此外，我們的方法簡單易行。我們的技術適用於以實時幀速處理實時視訊流，使其成為增強現實等互動式應用的有用工具。 

1、簡介（introduction）
影象閾值化基於畫素的特定特徵（例如強度值）來分割數字影象。目標是建立二值影象，將每個畫素分類為兩個類別之一，例如“暗”或“亮”。這是許多影象處理應用程式和一些計算機圖形應用程式中的常見任務。例如，它通常是基於標記的增強現實系統的第一步[Billinghurstet al。 2001;布拉德利和羅斯2004; Fiala 2005]，它已被用於高動態範圍攝影[Ward2003]。最基本的閾值處理方法是選擇固定的閾值並將每個畫素與該值進行比較。這些技術已在許多調查論文中進行了廣泛的描述和評估[Weszka andRosenfeld 1978; Palumbo等人。 1986; Sahoo等。 1988;李等人。 1990; Glasbey 1993;特里爾和耆那教1995; Sezginand Sankur 2004]。然而，如果照明在影象中在空間上變化或在視訊流中超時，則固定閾值經常失敗。

為了解釋照明的變化，常見的解決方案是自適應閾值處理。主要區別在於為影象中的每個畫素計算不同的閾值。該技術為照明變化提供了更強大的功能。存在許多自適應閾值方法[White和Rohrer 1983; Bernsen1986;帕克1991; Wellner 1993;楊等人。 1994; Shen和Ip 1997;陳等人。 1998; Savakis 1998; Sauvolaand Pietikainen 2000;楊和燕2000]。進一步的例子和比較可以在[Venkateswarlu andBoyle 1995; Sezgin和Sankur 2004]。我們使用積分影象提出了一種非常簡單明瞭的技術。我們的方法易於實現實時視訊流的實時效能。雖然我們的技術是以前方法的擴充套件[Wellner 1993]，但我們增強了強光照變化的穩健性。此外，我們提供清晰整潔的解決方案，而不會增加實施的複雜性。我們的技術也類似於White和Rohrer用於光學字元識別的閾值處理方法[White and Rohrer 1983]，但我們提出了一種針對實時視訊設計的實現方法。這項工作的動機是找到真正的現實應用程式。 Pintaric還提出了一種適用於增強現實標記的自適應閾值演算法[Pintaric 2003]，但是他的方法要求在前一幀中定位一個元素，以便技術正確地進行閾值處理。我們的演算法不做任何假設，更通用，適合在任何應用中使用。原始碼可在本文末尾列出的地址線上獲取。

2、背景 

2.1實時自適應閾值處理
在本文中，我們專注於從實時視訊流中自適應地閾值化影象。 為了保持實時效能，閾值演算法必須限制通過每個影象的迭代次數。 閾值處理通常是一個子任務，它構成了一個更大的過程的一部分。 例如，在增強現實中，必須對輸入影象進行分段以定位場景中用於動態建立相機設定的已知標記。 因此，簡單快速的自適應閾值技術是一個重要的工具

2.2積分影象
積分影象（也稱為summed-area table）是一種工具，當我們有一個從畫素到數值（比如灰度值）的對映函式f(x, y)，並且希望計算一個矩形區域內的函式值的和時，積分圖是一個非常高效的工具。已應用積分影象的示例包括紋理對映[Crow 1984]，影象中的人臉檢測[Viola and Jones 2004]和立體對應[Veksler 2003]。在沒有積分影象的情況下，我們計算每個矩形視窗中畫素點的對映函式的和，需要通過分別計算每個畫素的函式值最後疊加實現。但是，如果我們需要計算多個重疊矩形視窗的總和，為了降低時間複雜度和操作次數，我們可以使用積分影象。

為了計算積分影象，我們在每個位置I（x，y）儲存左邊和上面畫素（x，y）的所有f（x，y）項的總和。 對於每個畫素，使用以下等式線上性時間內完成（考慮邊界情況），

圖2（左和中）說明了積分影象的計算。 一旦我們得到積分影象，任何具有左上角（x1，y1）和右下角（x2，y2）的矩形的函式的總和可以使用以下等式計算，計算時間不穩定。

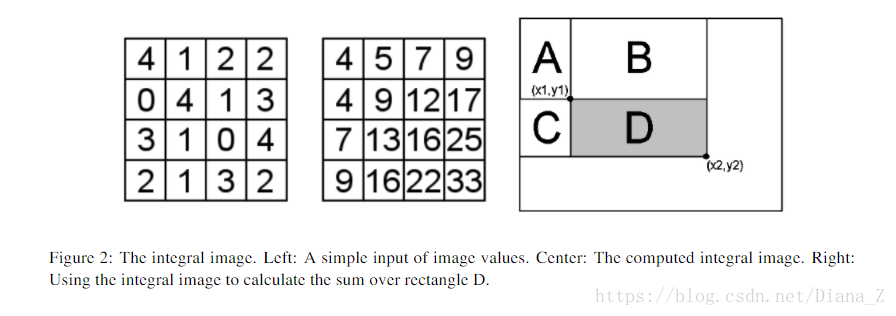
圖2（右）說明使用等式2計算矩形D上的f（x，y）之和相當於計算矩形上的和（A + B + C + D） - （A + B） - （A+ C）+ A。

圖2：積分影象。 左：影象值的簡單輸入。 中心：計算的積分影象。 右：使用積分影象計算矩形D的總和。

3、技術

    我們的自適應閾值技術是Wellner方法的簡單擴充套件[WELNER 1993 ]。Welnne演算法的主要思想是將每個畫素與周圍畫素的平均值進行比較。特別地，在遍歷影象時計算了最後一個畫素的近似移動平均值。如果當前畫素的值比平均值低百分之t，那麼它被設定為黑色，否則它被設定為白色。這種方法的工作是將畫素與附近畫素的平均值進行比較，從而保持硬對比線，忽略軟梯度變化。這種方法的優點是隻需要遍歷一次影象。WELNER使用1／8倍的影象寬度來表示s的值，t=15。然而，這種方法的一個問題是它依賴於畫素的掃描順序。此外，由於鄰域樣本在各個方向上不均勻分佈，所以在使用平均步長並不是一個很好的表現形式。通過使用積分影象（和骶一個額外的迭代通過影象），我們提出了一個解決方案，不遭受這些問題。我們的技術是乾淨的，直截了當的，易於編碼，併產針對不同的處理方式產生生相同的輸出。我們不是計算最後看到的s個畫素的平均值，而是計算以每個畫素為中心的s x s畫素視窗的平均值。 這是比較好的平均值，因為它考慮了所有邊上的相鄰畫素。利用積分影象進行平均計算的時間是線性的。我們在第一次遍歷影象的時候計算積分影象。在第二遍中，我們利用積分影象計算每個畫素的s x s的平均值，使用時間為常量，然後進行比較。如果當前畫素的值小於這個平均值，則將其設定為黑色，否則它被設定為白色。下面的虛擬碼展示了輸入影象、輸出二值影象、影象寬度W和影象高度H的關係。0

procedure AdaptiveThreshold(in,out,w,h)
    for i=0 to w do
        sum ← 0
        for j=0 to h do
            sum ← sum + in[i,j]
            if i=0 then
                int Img[i,j]←sum
            else
                int Img[i,j]←int Img[i−1,j] + sum
            end if
        end for
    end for 
    for i=0 to w do
        for j=0 to h do
            x1←i−s/2{border checking is not shown}
            x2←i+s/2
            y1←j−s/2
            y2←j+s/2
            count ←(x2−x1)×(y2−y1)
            sum ←intImg[x2,y2]−intImg[x2,y1−1]−intImg[x1−1,y2] + intImg[x1−1,y1−1]
            if (in[i,j]×count)≤(sum ×(100 −t)/100) then
                out[i,j]←0
            else
                out[i,j]←255
            end if
        end for
    end for 

這是我自己根據虛擬碼寫的matlab程式碼 

I=imread('./pic/2.jpg');
figure
imshow(I)
I=rgb2gray(I);
I=double(I);
sz=size(I);
h=sz(1);
w=sz(2);
in=I;
s=h/8;
t=20;
for i=1:w
    sum =0;
    for j=1:h
        sum=sum + in(j,i);
        if i==1
            intImg(j,i)=sum;
        else
            intImg(j,i)=intImg(j,i-1) + sum;
        end
    end
end
for i=1:w
    for j=1:h
        x1=max(i-round(s/2),2); %{border checking is not shown}
        x2=min(i+round(s/2),w);
        y1=max(j-round(s/2),2);
        y2=min(j+round(s/2),h);
        count =(x2-x1)*(y2-y1);
        sum =intImg(y2,x2)-intImg(y1-1,x2)-intImg(y2,x1-1) + intImg(y1-1,x1-1);
        if (in(j,i)*count)<=(sum *(100 -t)/100) 
            out(j,i)=0;
        else
            out(j,i)=255;
        end
    end
end
figure
imshow(out)

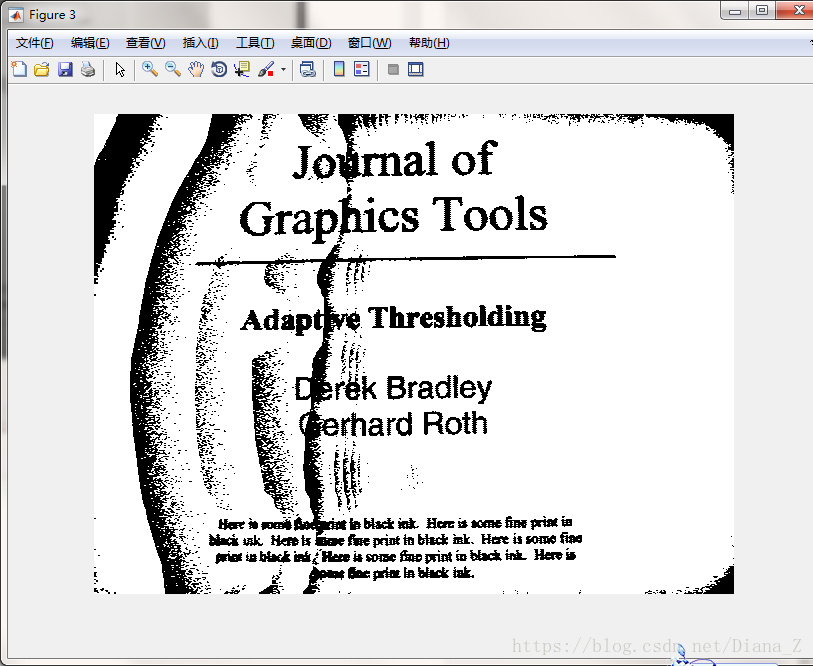
以及測試結果:

原圖

s=h/8,t=10

s=h/16,t=10

s=h/8,t=15

s=h/16,t=15

s=h/8,t=20