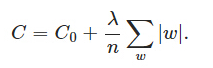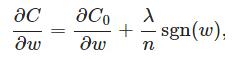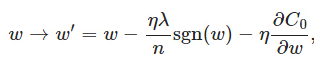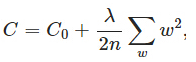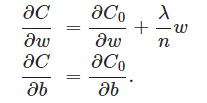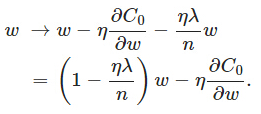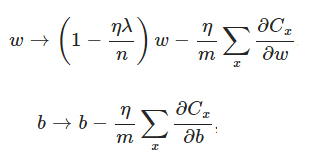一.過擬合

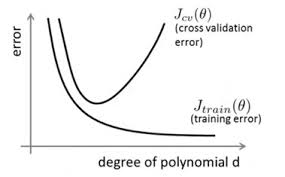
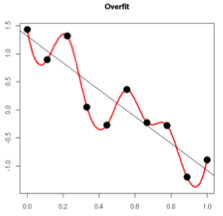
在訓練資料不夠多時，或者over-training時，經常會導致over-fitting（過擬合）。其直觀的表現如下圖所所示。

隨著訓練過程的進行，模型複雜度，在training data上的error漸漸減小。可是在驗證集上的error卻反而漸漸增大——由於訓練出來的網路過擬合了訓練集，對訓練集以外的資料卻不work。

在機器學習演算法中，我們經常將原始資料集分為三部分：訓練集（training data）、驗證集（validation data）、測試集（testing data）。

1.validation data是什麼？

它事實上就是用來避免過擬合的。在訓練過程中，我們通經常使用它來確定一些超引數（比方,

2.防止過擬合方法主要有：

1.正則化（Regularization）（L1和L2）

2.資料增強（Data augmentation），也就是增加訓練資料樣本

3.Dropout

4.early stopping

二、正則化

正則化（Regularization）包含L1、L2（L2 regularization也叫權重衰減，weight decay）

1.L1 regularization

在原始的代價函式後面加上一個L1正則化項,即全部權重w的絕對值的和，再乘以λ/n（這裡不像L2正則化項那樣，須要再乘以1/2）。

先計算導數：

上式中sgn(w)表示 w 的符號，那麼權重w的更新規則為：

比原始的更新規則多出了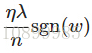這一項。

當w為正時，sgn(w)>0, 則更新後的w變小。

當w為負時，sgn(w)>0, 則更新後的w變大——因此它的效果就是讓w往0靠，使網路中的權重儘可能為0，也就相當於減小了網路複雜度，防止過擬合。

另外，上面沒有提到一個問題，當w為0時怎麼辦？當w等於0時，|W|是不可導的。所以我們僅僅能依照原始的未經正則化的方法去更新w，這就相當於去掉 η*λ*sgn(w)/n 這一項，所以我們能夠規定sgn(0)=0，這樣就把 w=0 的情況也統一進來了。

（在程式設計的時候，令sgn(0)=0,sgn(w>0)=1,sgn(w<0)=-1）

2. L2 regularization（權重衰減）

L2正則化就是在代價函式後面再加上一個正則化項：

C0代表原始的代價函式，後面那一項就是L2正則化項。它是這樣來的：全部引數 w 的平方和，除以訓練集的樣本大小n。

λ 就是正則項係數，權衡正則項與C0項的比重。另外另一個係數1/2，1/2經常會看到，主要是為了後面求導的結果方便，後面那一項求導會產生一個2,與1/2相乘剛好湊整。L2正則化項是怎麼避免overfitting的呢？我們推導一下看看，先求導：

能夠發現L2正則化項對 b 的更新沒有影響，可是對於w的更新有影響:

在不使用L2正則化時。求導結果中 w 前係數為 1，經變化後w前面係數為 1−ηλ/n ，由於η、λ、n都是正的。所以 1−ηλ/n小於1，它的效果是減小w，這也就是權重衰減（weight decay）的由來。

當然考慮到後面的導數項，w 終於的值可能增大也可能減小。

另外，必須提一下，對於基於mini-batch的隨機梯度下降，w 和 b 更新的公式跟上面給出的有點不同：

對照上面 w 的更新公式。能夠發現後面那一項變了，變成全部導數加和，乘以η再除以m，m是一個mini-batch中樣本的個數。

在此我們僅僅是解釋了L2正則化項有讓w“變小”的效果，可是還沒解釋為什麼w“變小”能夠防overfitting？

一個所謂“顯而易見”的解釋就是：更小的權值w，從某種意義上說，表示網路的複雜度更低，對資料的擬合剛剛好（這個法則也叫做奧卡姆剃刀），而在實際應用中，也驗證了這一點，L2正則化的效果往往好於未經正則化的效果。當然，對於非常多人（包含我）來說，這個解釋似乎不那麼顯而易見，所以這裡加入一個略微數學一點的解釋（引自知乎）：

過擬合的時候，擬合函式的係數往往非常大，為什麼？例如以下圖所看到的，過擬合。就是擬合函式須要顧忌每個點。終於形成的擬合函式波動非常大。在某些非常小的區間裡，函式值的變化非常劇烈。

這就意味著函式在某些小區間裡的導數值（絕對值）非常大，由於自變數值可大可小，所以僅僅有係數足夠大，才幹保證導數值非常大。而L2正則化是通過約束引數的範數使其不要太大，所以能夠在一定程度上降低過擬合情況。

3.在什麼情況下使用L1,什麼情況下使用L2？

L1和L2的差別，為什麼一個讓絕對值最小，一個讓平方最小，會有那麼大的差別呢？我看到的有兩種幾何上直觀的解析：

（1）下降速度：

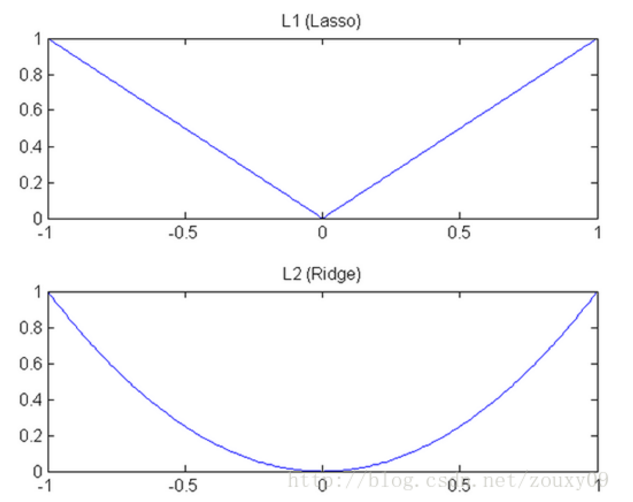
我們知道，L1和L2都是規則化的方式，我們將權值引數以L1或者L2的方式放到代價函式裡面去。然後模型就會嘗試去最小化這些權值引數。而這個最小化就像一個下坡的過程，L1和L2的差別就在於這個“坡”不同，如下圖：L1就是按絕對值函式的“坡”下降的，而L2是按二次函式的“坡”下降。所以實際上在0附近，L1的下降速度比L2的下降速度要快，所以會非常快得降到0。不過我覺得這裡解釋的不太中肯，當然了也不知道是不是自己理解的問題。

L1稱Lasso，L2稱Ridge。

總結就是：L1會趨向於產生少量的特徵，而其他的特徵都是0，而L2會選擇更多的特徵，這些特徵都會接近於0。Lasso在特徵選擇時候非常有用，而Ridge就只是一種規則化而已。

三. 資料集擴增（data augmentation）

訓練模型有時候不是由於演算法好贏了，而是由於擁有海量的資料才贏了。”

不記得原話是哪位大牛說的了，hinton？從中可見訓練資料有多麼重要，特別是在深度學習方法中，海量的訓練資料，意味著能夠用更深的網路，訓練出更好的模型。

既然這樣，收集大量資料不就OK啦？假設能夠收集很多其它能夠用的資料，當然好。可是非常多時候，收集很多其它的資料意味著須要耗費很多其它的人力物力。尤其在對資料集進行人工標註的同學就知道，效率特別低，簡直是粗活。

所以。能夠在原始資料上做些改動，得到很多其它的資料，以圖片資料集舉例，能夠做各種變換，如：

• 將原始圖片旋轉一個小角度

• 加入隨機噪聲

• 一些有彈性的畸變（elastic distortions），論文《Best practices for convolutional neural networks applied to visual document analysis》對MNIST做了各種變種擴增。

• 擷取（crop）原始圖片的一部分，比方DeepID中，從一副人臉圖中，截取出了100個小patch作為訓練資料，極大地添加了資料集。

  感興趣的能夠看《Deep learning face representation from predicting 10,000 classes》.

大量訓練資料意味著什麼？

用50000個MNIST的樣本訓練SVM得出的accuracy94.48%，用5000個MNIST的樣本訓練KNN得出accuracy為93.24%，所以很多其它的資料能夠使演算法表現得更好。

在機器學習中，演算法本身並不能決出勝負，不能武斷地說這些演算法誰優誰劣，由於資料對演算法效能的影響非常大。

四.Dropout

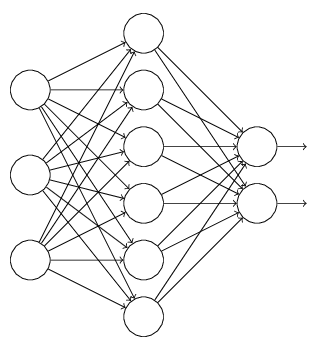
L1、L2正則化是通過改動代價函式來實現的，而Dropout則是通過改動神經網路本身來實現的，它是在訓練網路時用的一種技巧（trike），它的流程例如以下：

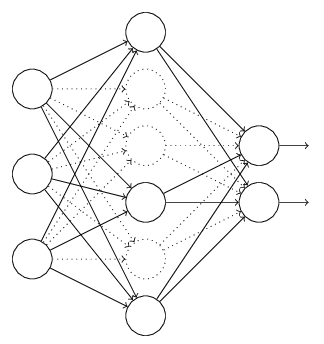
假設我們要訓練上圖這個網路，在訓練開始時，我們隨機地“刪除”一部分的隱層單元，視它們為不存在，得到例如以下的網路：

保持輸入輸出層不變，依照BP演算法更新上圖神經網路中的權值（虛線連線的單元不更新，由於它們被“暫時刪除”了）。

以上就是一次迭代的過程，在第二次迭代中，也用相同的方法，僅僅只是這次刪除的那一部分隱層單元，跟上一次刪除掉的肯定是不一樣的。由於我們每一次迭代都是“隨機”地去刪掉一部分。

第三次、第四次……都是這樣，直至訓練結束。

以上就是Dropout，它為什麼有助於防止過擬合呢？能夠簡單地這樣解釋，運用了dropout的訓練過程，相當於訓練了非常多個僅僅有部分隱層單元的神經網路，每個這種半數網路，都能夠給出一個分類結果，這些結果有的是正確的，有的是錯誤的。

隨著訓練的進行，大部分半數網路都能夠給出正確的分類結果。那麼少數的錯誤分類結果就不會對終於結果造成大的影響。

刪除神經單元，不工作，通常keep_prob取0.5

在程式設計時可以利用TensorFlow中 DropoutWrappera函式

在訓練過程引入Dropout 策略，其Dropout層保留節點比例（keep_prob）,每批資料輸入時神經網路中的每個單元會以1-keep_prob的概率不工作，防止過擬合。

lstmCell = tf.contrib.rnn.DropoutWrapper(cell=lstmCell, output_keep_prob=0.5)

更加深入地理解。能夠看看Hinton和Alex兩牛2012的論文《ImageNet Classification with Deep Convolutional Neural Networks》

五、提前終止（Early stopping）

    對模型進行訓練的過程即是對模型的引數進行學習更新的過程，這個引數學習的過程往往會用到一些迭代方法，如梯度下降（Gradient descent）學習演算法。Early stopping便是一種迭代次數截斷的方法來防止過擬合的方法，即在模型對訓練資料集迭代收斂之前停止迭代來防止過擬合。 

  Early stopping方法的具體做法是，在每一個Epoch結束時（一個Epoch集為對所有的訓練資料的一輪遍歷）計算validation data的accuracy，當accuracy不再提高時，就停止訓練。這種做法很符合直觀感受，因為accurary都不再提高了，在繼續訓練也是無益的，只會提高訓練的時間。那麼該做法的一個重點便是怎樣才認為validation accurary不再提高了呢？並不是說validation accuracy一降下來便認為不再提高了，因為可能經過這個Epoch後，accuracy降低了，但是隨後的Epoch又讓accuracy又上去了，所以不能根據一兩次的連續降低就判斷不再提高。一般的做法是，在訓練的過程中，記錄到目前為止最好的validation accuracy，當連續10次Epoch（或者更多次）沒達到最佳accuracy時，則可以認為accuracy不再提高了。此時便可以停止迭代了（Early Stopping）。這種策略也稱為“No-improvement-in-n”，n即Epoch的次數，可以根據實際情況取，如10、20、30……

六、從資料預處理角度

1.對原始資料通過PCA， t-SNE等降維技術進行降維處理

2.平衡不同類資料的權重等

參考：