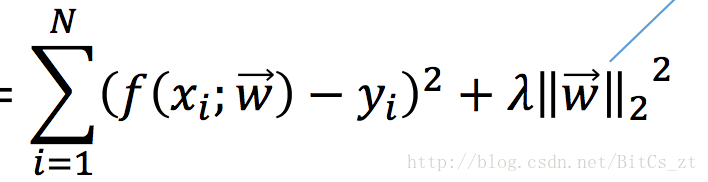在用機器學習模型解決實際問題時，時刻離不開“擬合”（fitting）一詞，擬合可以看做挖掘樣本集與對應標籤的規律。模型的預測值和樣本的真實標籤之間的差異稱為“誤差”（error），在實際問題中，我們通常在訓練集上訓練模型，由此產生“訓練誤差”（training error），然後將模型運用於測試集上，由此產生“泛化誤差”（generalization error）。我們希望得到一個泛化誤差小的模型，即處理新樣本時儘可能預測準確。

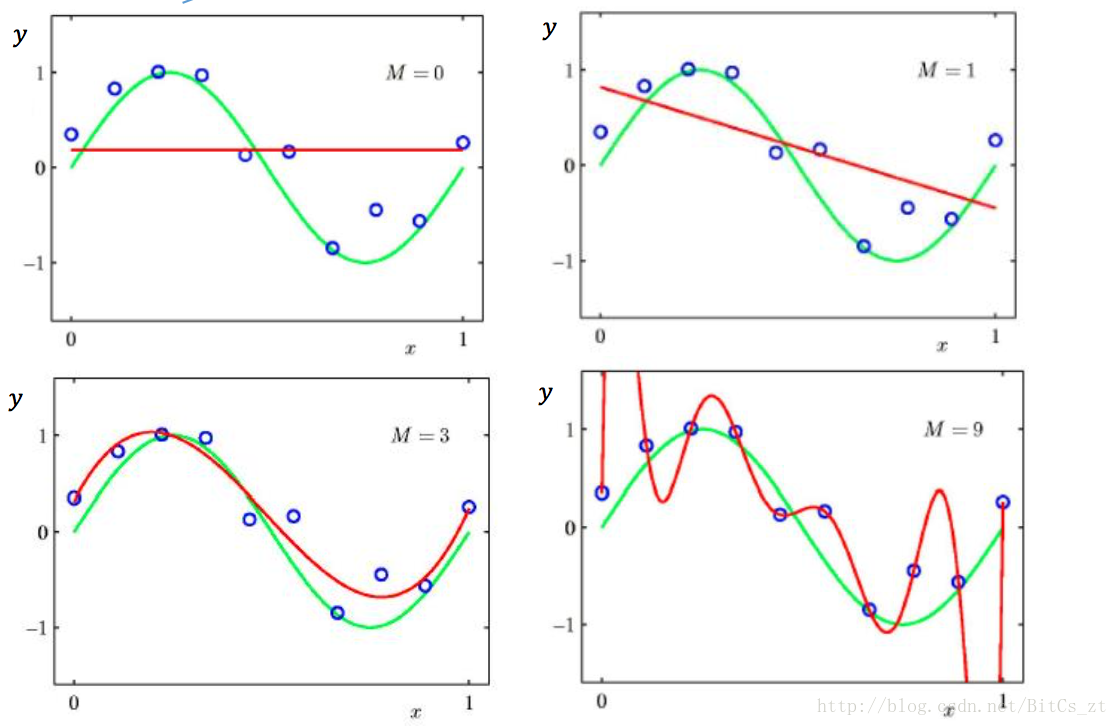
在大多數情況下，我們能夠通過各種方式得到一個經驗誤差很小的模型，即在訓練集上達到極高的準確率。但由於訓練集和測試集並不完全相同（資料可能來自不同分佈，或同一分佈下的取樣差異），導致我們在訓練集上的擬合過度，挖掘出的規律只適用於訓練集而不適用於所有樣本，把訓練樣本的一些特點當成了所有樣本都具有的一般性質。這種現象稱為“過擬合”（overfitting）。與之相對的是“欠擬合”（underfitting），即對訓練樣本的性質挖掘不夠。

用多項式函式來模擬sin函式，M表示多項式最高次項的次數。可以看到，當M=1、3時為欠擬合，沒有挖掘到sin函式的一般規律，而當M=9時為過擬合，過分追求了訓練誤差最小。

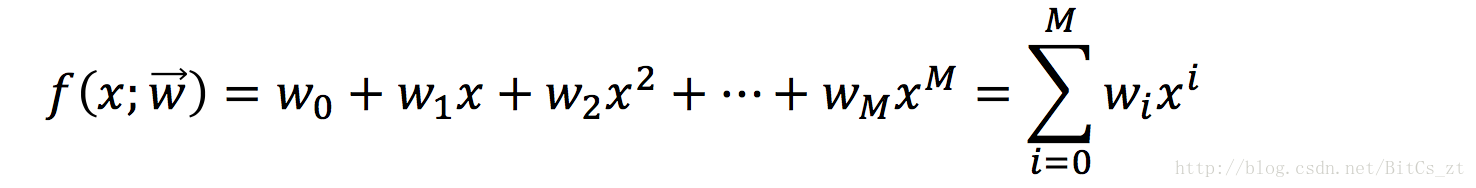
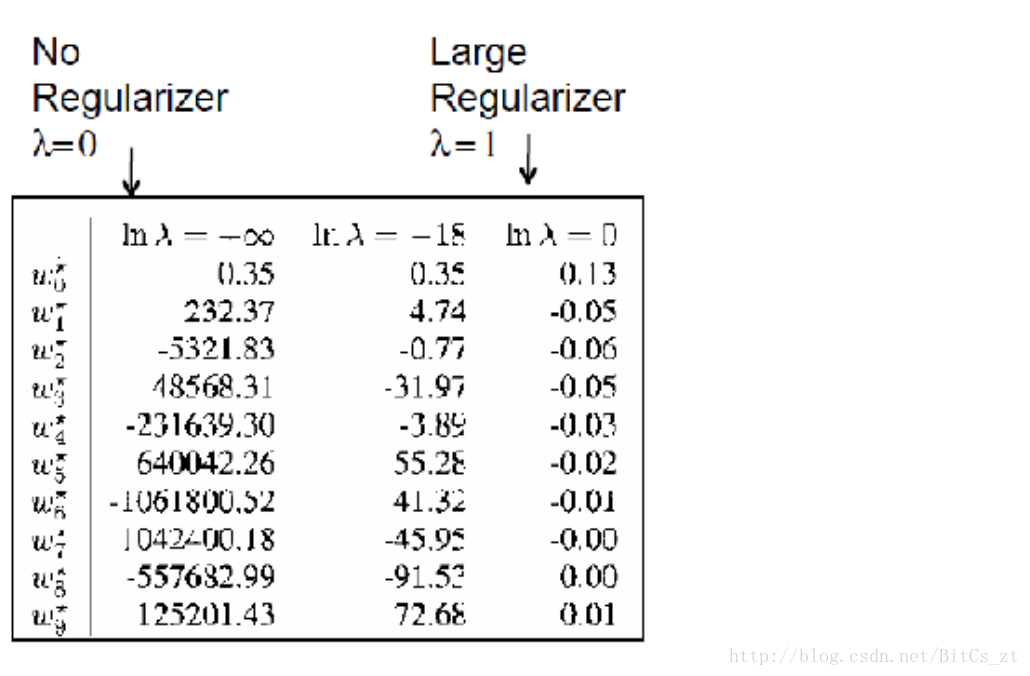
可以看到，在過擬合情況下，模型引數值巨大。若此時樣本屬性值稍有變化，乘以巨大的引數，便會使模型預測結果有巨大的浮動，導致泛化誤差變大。

有多種因素可能導致過擬合，最常見的原因是由於模型學習能力過於強大，如神經網路理論上可以逼近任何函式，自然也就能擬合所有訓練資料。而欠擬合通常是由於模型學習能力弱，實際中比較容易解決，如加強模型表示能力或者更換更強有力的模型。解決過擬合問題是機器學習面臨的關鍵障礙，好比在崎嶇的山路上賽車，如果速度慢（欠擬合）只需要加速即可，而速度過快（過擬合）只會車毀人亡，找到合適的車速，既能不衝出賽道又能快速到達終點是很困難的。

想要得到泛化誤差小的模型，無外乎兩點。首先需要一個能很好擬合訓練資料的模型（避免欠擬合），然後該模型必須能適用於測試集（不要太複雜的模型）。因此，在訓練過程中，我們不僅要減小訓練誤差，還要同時控制模型複雜度，即我們訓練時最小化的目標是：

前一項即訓練誤差，通常也稱為“經驗風險”（empirical risk）。後一項為正則化項（regularization），也稱為“結構風險”（structure risk），λ為控制引數。應用到上述問題中：

本例中正則化項為L2範數，在加入了對模型的限制條件後再進行訓練，可以看到引數數值都被限制得比較小，此時若樣本屬性值發生變化，乘以小的引數，也不會使預測結果有太大波動，使泛化誤差變小。

值得一提的是，除了控制模型複雜度從而解決過擬合問題，我們還可以增加訓練資料量。當訓練資料增多時，訓練資料分佈也就越接近真實資料分佈，挖掘出的規律越可能適用於全部資料，資料越多，強模型越能發揮威力。

上面我們只是從直觀的角度理解了擬合問題、訓練誤差和泛化誤差，下面利用偏差-方差分解對上述問題進行理論分析。

令

• x為測試樣本
• yD為x在資料集（非訓練集）中的標籤
• y為x的真實標記
• f(x;D)為訓練集D上學得的模型f在x上的預測輸出

則模型的期望預測為：

使用樣本數相同的不同訓練集產生的方差（varience）為：

噪聲為：

期望輸出與真實標記的差別稱為偏差（bias），為：

假定噪聲期望為0，即：

則演算法的期望泛化誤差可分解為：

即泛化誤差可分解為偏差、方差和噪聲之和。其中f̂ (x)表示在不同訓練集下預測值的平均，可視為預測值。偏差實際上衡量的是預測值和真實標籤的差距，即預測得準不準，可用來衡量訓練誤差。而方差衡量的是模型在不同樣本集上預測結果的浮動程度，即刻畫了資料擾動造成的影響，可用來衡量泛化效能。

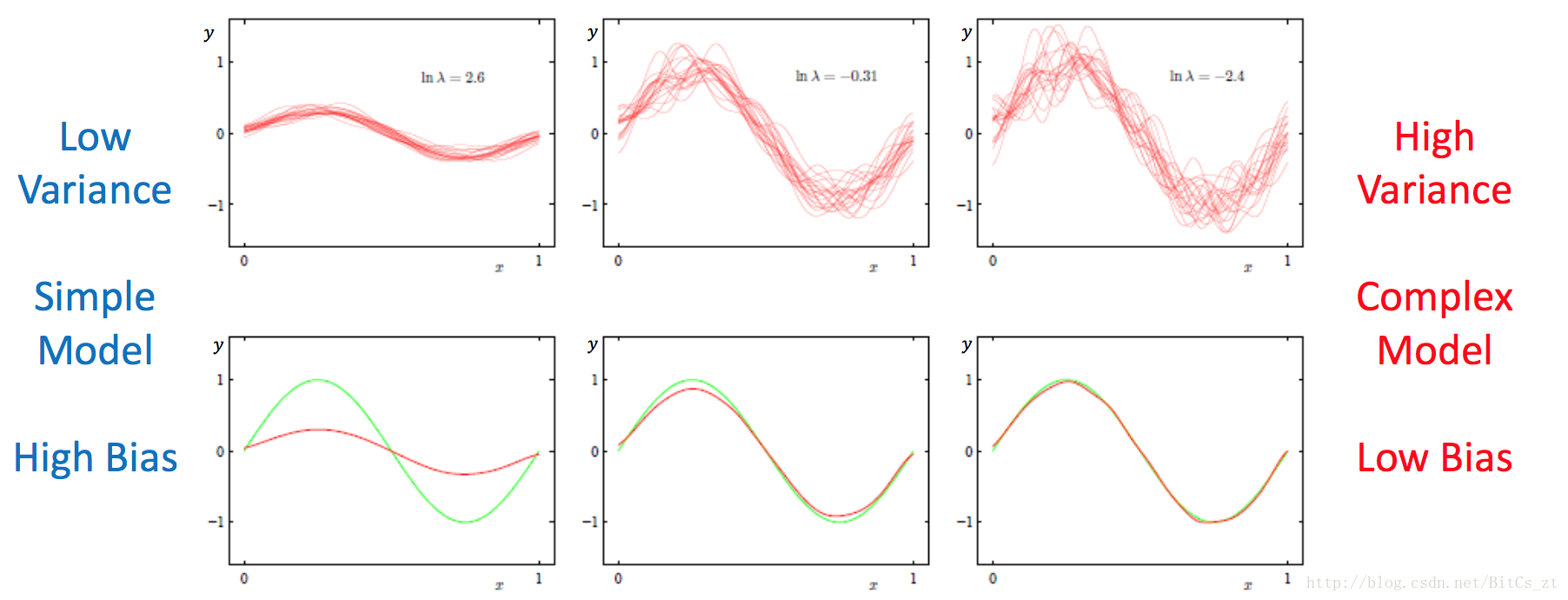
可以看到，給定特定的模型（演算法）和具體的問題，期望泛化誤差是一定的，降低bias將增加varience，反之亦然。偏差-方差的控制存在一個trade-off，強有力的模型能降低bias，但可能會使varience增加，泛化效能差，對應的是過擬合的情況。而簡單的模型（加正則項的強模型）可能在訓練誤差大，bias高，但可能泛化效能強，varience相對較低，對應的則是欠擬合的情況。如下圖所示：

實際上，我們只能通過不斷的實驗調節引數，最終找到較好的折中方案。這不僅需要我們對模型有深刻的認識，知道如何去限制或釋放模型的能力，更需要我們對資料有深刻的認識，選擇出適用於特定問題的模型來解決問題。