傳送門

題面：

D. Glider

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A plane is flying at a constant height of hh meters above the ground surface. Let's consider that it is flying from the point (−109,h)(−109,h) to the point (109,h)(109,h) parallel with OxOx axis.

A glider is inside the plane, ready to start his flight at any moment (for the sake of simplicity let's consider that he may start only when the plane's coordinates are integers). After jumping from the plane, he will fly in the same direction as the plane, parallel to OxOx axis, covering a unit of distance every second. Naturally, he will also descend; thus his second coordinate will decrease by one unit every second.

There are ascending air flows on certain segments, each such segment is characterized by two numbers x1x1 and x2x2 (x1<x2x1<x2) representing its endpoints. No two segments share any common points. When the glider is inside one of such segments, he doesn't descend, so his second coordinate stays the same each second. The glider still flies along OxOx axis, covering one unit of distance every second.

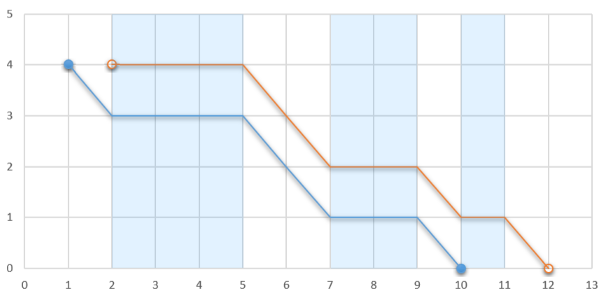If the glider jumps out at 11, he will stop at 1010. Otherwise, if he jumps out at 22, he will stop at 1212.

Determine the maximum distance along OxOx axis from the point where the glider's flight starts to the point where his flight ends if the glider can choose any integer coordinate to jump from the plane and start his flight. After touching the ground the glider stops altogether, so he cannot glide through an ascending airflow segment if his second coordinate is 00.

Input

The first line contains two integers nn and hh (1≤n≤2⋅105,1≤h≤109)(1≤n≤2⋅105,1≤h≤109) — the number of ascending air flow segments and the altitude at which the plane is flying, respectively.

Each of the next nn lines contains two integers xi1xi1 and xi2xi2 (1≤xi1<xi2≤109)(1≤xi1<xi2≤109) — the endpoints of the ii-th ascending air flow segment. No two segments intersect, and they are given in ascending order.

Output

Print one integer — the maximum distance along OxOx axis that the glider can fly from the point where he jumps off the plane to the point where he lands if he can start his flight at any integer coordinate.

Examples

input

Copy

3 4
2 5
7 9
10 11

output

Copy

10

input

Copy

5 10
5 7
11 12
16 20
25 26
30 33

output

Copy

18

input

Copy

1 1000000000
1 1000000000

output

Copy

1999999999

Note

In the first example if the glider can jump out at (2,4)(2,4), then the landing point is (12,0)(12,0), so the distance is 12−2=1012−2=10.

In the second example the glider can fly from (16,10)(16,10) to (34,0)(34,0), and the distance is 34−16=1834−16=18.

In the third example the glider can fly from (−100,1000000000)(−100,1000000000) to (1999999899,0)(1999999899,0), so the distance is 1999999899−(−100)=19999999991999999899−(−100)=1999999999.

題意：

    你現在處於高度為h的地方，每秒y座標會減少1，x座標會增加1，而現在會有n個氣流區[l,r]，在每個氣流區中，你的y座標不會改變，你的x座標每秒會增加1。（保證所給出的氣流兩兩之間沒有交集）現在你可以從x軸上的任意一點下落，現在問你最遠的飛行路徑。

題目分析：

    因為題目中保證了氣流區兩兩不相交，因此我們就可以省下來很多討論的功夫。

    因此，此時只會存在（1）衝過某個氣流區後直接落地，（2）衝過某個氣流區後，又經過另一個氣流區，兩種情況。

    因此我們可以採用雙指標，分別記錄終點和起點的位置，並不斷的對上述兩種情況討論，最後列舉所有的氣流，記錄一下最大值即可。

程式碼：

#include <bits/stdc++.h>
#define maxn 200005
using namespace std;
struct Node{
    int l,r;
}q[maxn];
typedef long long ll;
int main()
{
    ll n,h;
    cin>>n>>h;
    for(int i=0;i<n;i++){
        scanf("%I64d%I64d",&q[i].l,&q[i].r);
    }
    ll l,r,tmp1,tmp2;
    l=q[0].l,r=q[0].r+h;//首先l指標先指向第一個氣流的起點，r指標指向落點
    ll ans=h;
    tmp1=tmp2=0;
    while(tmp1<n){//列舉每一個氣流
        while(tmp2+1<n&&q[tmp2+1].l<r){
        //如果下一個氣流的左區間在終點前，則證明出現情況2，則將終點加上該氣流的區間大小
            tmp2++;
            r+=q[tmp2].r-q[tmp2].l;
        }
        ans=max(ans,r-l);//記錄r-l的最大值
        tmp1++;
        l=q[tmp1].l;//將起點置為下一個氣流的起點
        r+=q[tmp1].l-q[tmp1-1].r;   //加上氣流與氣流之間的大小
    }
    cout<<ans<<endl;
}