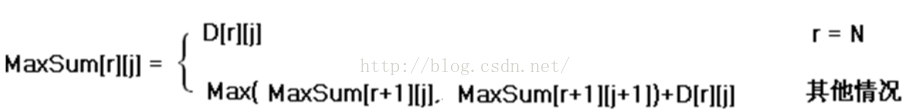從 poj 1163( The Triangle )教你徹底學會動態規劃——入門篇
動態規劃相信大家都知道,動態規劃演算法也是新手在剛接觸演算法設計時很苦惱的問題,有時候覺得難以理解,但是真正理解之後,就會覺得動態規劃其實並沒有想象中那麼難。網上也有很多關於講解動態規劃的文章,大多都是敘述概念,講解原理,讓人覺得晦澀難懂,即使一時間看懂了,發現當自己做題的時候又會覺得無所適從。我覺得,理解演算法最重要的還是在於練習,只有通過自己練習,才可以更快地提升。話不多說,接下來,下面我就通過一個例子來一步一步講解動態規劃是怎樣使用的,只有知道怎樣使用,才能更好地理解,而不是一味地對概念和原理進行反覆琢磨。
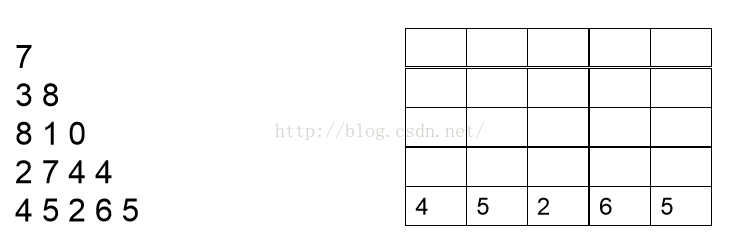
首先,我們看一下這道題(此題目來源於北大POJ):
數字三角形(POJ1163)
在上面的數字三角形中尋找一條從頂部到底邊的路徑,使得路徑上所經過的數字之和最大。路徑上的每一步都只能往左下或 右下走。只需要求出這個最大和即可,不必給出具體路徑。 三角形的行數大於1小於等於100,數字為 0 - 99
輸入格式:
5 //表示三角形的行數 接下來輸入三角形
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
要求輸出最大和
接下來,我們來分析一下解題思路:
首先,肯定得用二維陣列來存放數字三角形
然後我們用
我們用MaxSum(r , j)表示從D(r , j)到底邊的各條路徑中(當然也可以說成是從底邊到D(r , j)的最佳路徑),最佳路徑的數字之和。
因此,此題的最終問題就變成了求 MaxSum(1,1)。(這裡是說陣列從[1,1]開始存。[0,0]直接空掉)
當我們看到這個題目的時候,首先想到的就是可以用簡單的遞迴來解題:
D(r , j)出發,下一步只能走D(r+1 , j)或者D(r+1 , j+1)。故對於N行的三角形,我們可以寫出如下的遞迴式:
if ( r == N) MaxSum(r,j) = D(r,j) //因為是從底邊往上走,所以最後一層(即是底邊)為最大值。 else MaxSum(r,j) = Max{ MaxSum(r+1,j), MaxSum(r+1,j+1) } + D(r,j)
根據上面這個簡單的遞迴式,我們就可以很輕鬆地寫出完整的遞迴程式碼:
#include <iostream>
#include <algorithm>
#define MAX 101
using namespace std;
int D[MAX][MAX];
int n;
int MaxSum(int i, int j){
if(i==n)
return D[i][j];
int x = MaxSum(i+1,j);
int y = MaxSum(i+1,j+1);
return max(x,y)+D[i][j];
}
int main(){
int i,j;
cin >> n;
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
cin >> D[i][j];
cout << MaxSum(1,1) << endl;
} 對於如上這段遞迴的程式碼,當我提交到POJ時,會顯示如下結果:
對的,程式碼執行超時了,為什麼會超時呢?
答案很簡單,因為我們重複計算了,當我們在進行遞迴時,計算機幫我們計算的過程如下圖:
就拿第三行數字1 來說,當我們計算從第2行 的數字3 開始的MaxSum時會計算出從1開始的MaxSum,當我們計算從第二行的數字8開始的MaxSum的時候又會計算一次從1開始的MaxSum,也就是說有重複計算。這樣就浪費了大量的時間。也就是說如果採用遞規的方法,深度遍歷每條路徑,存在大量重複計算。則時間複雜度為 2的n次方,對於 n = 100 行,肯定超時。
接下來,我們就要考慮如何進行改進,我們自然而然就可以想到如果每算出一個MaxSum(r,j)就儲存起來,下次用到其值的時候直接取用,則可免去重複計算。那麼可以用n方的時間複雜度完成計算。因為三角形的數字總數是 n(n+1)/2
根據這個思路,我們就可以將上面的程式碼進行改進,使之成為記憶遞迴型的動態規劃程式:
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int maxSum[MAX][MAX]; //記憶動態規劃開闢的陣列///*
int MaxSum(int i, int j){
if( maxSum[i][j] != -1 )
return maxSum[i][j]; //記憶遞迴動態規劃///*
if(i==n)
maxSum[i][j] = D[i][j];
else{
int x = MaxSum(i+1,j);
int y = MaxSum(i+1,j+1);
maxSum[i][j] = max(x,y)+ D[i][j];
}
return maxSum[i][j];
}
int main(){
int i,j;
cin >> n;
for(i=1;i<=n;i++)
for(j=1;j<=i;j++) {
cin >> D[i][j];
maxSum[i][j] = -1;
}
cout << MaxSum(1,1) << endl;
} 當我們提交如上程式碼時,結果就是一次AC
雖然在短時間內就AC了。但是,我們並不能滿足於這樣的程式碼,因為遞迴總是需要使用大量堆疊上的空間,很容易造成棧溢位,我們現在就要考慮如何把遞迴轉換為遞推,讓我們一步一步來完成這個過程。
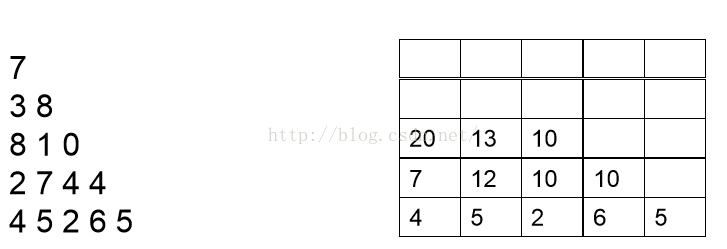
我們首先需要計算的是最後一行,因此可以把最後一行直接寫出,如下圖:
現在開始分析倒數第二行的每一個數,現分析數字2,2可以和最後一行4相加,也可以和最後一行的5相加,但是很顯然和5相加要更大一點,結果為7,我們此時就可以將7儲存起來,然後分析數字7,7可以和最後一行的5相加,也可以和最後一行的2相加,很顯然和5相加更大,結果為12,因此我們將12儲存起來。以此類推。。我們可以得到下面這張圖:
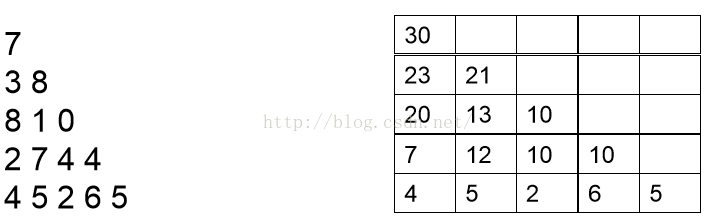
然後按同樣的道理分析倒數第三行和倒數第四行,最後分析第一行,我們可以依次得到如下結果:
上面的推導過程相信大家不難理解,理解之後我們就可以寫出如下的遞推型動態規劃程式:
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int maxSum[MAX][MAX];
int main(){
int i,j;
cin >> n;
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
cin >> D[i][j];
for( int i = 1;i <= n; ++ i )
maxSum[n][i] = D[n][i];
for( int i = n-1; i>= 1; --i )
for( int j = 1; j <= i; ++j )
maxSum[i][j] = max(maxSum[i+1][j],maxSum[i+1][j+1]) + D[i][j];
cout << maxSum[1][1] << endl;
} 我們的程式碼僅僅是這樣就夠了嗎?當然不是,我們仍然可以繼續優化,而這個優化當然是對於空間進行優化,其實完全沒必要用二維maxSum陣列儲存每一個MaxSum(r,j),只要從底層一行行向上遞推,那麼只要一維陣列maxSum[100]即可,即只要儲存一行的MaxSum值就可以。
對於空間優化後的具體遞推過程如下:
接下里的步驟就按上圖的過程一步一步推導就可以了。進一步考慮,我們甚至可以連maxSum陣列都可以不要,直接用D的第n行直接替代maxSum即可。但是這裡需要強調的是:雖然節省空間,但是時間複雜度還是不變的。
依照上面的方式,我們可以寫出如下程式碼:
#include <iostream>
#include <algorithm>
using namespace std;
#define MAX 101
int D[MAX][MAX];
int n;
int * maxSum;
int main(){
int i,j;
cin >> n;
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
cin >> D[i][j];
maxSum = D[n]; //maxSum指向第n行
for( int i = n-1; i>= 1; --i )
for( int j = 1; j <= i; ++j )
maxSum[j] = max(maxSum[j],maxSum[j+1]) + D[i][j];
cout << maxSum[1] << endl;
}接下來,我們就進行一下總結:
遞迴到動態規劃的一般轉化方法
遞迴函式有n個引數,就定義一個n維的陣列,陣列的下標是遞迴函式引數的取值範圍,陣列元素的值是遞迴函式的返回值,這樣就可以從邊界值開始, 逐步填充陣列,相當於計算遞迴函式值的逆過程。
動態規劃解題的一般思路
1 將原問題分解為子問題
- 把原問題分解為若干個子問題,子問題和原問題形式相同或類似,只不過規模變小了。子問題都解決,原問題即解決(數字三角形例)。
- 子問題的解一旦求出就會被儲存,所以每個子問題只需求解一次。
2 確定狀態
- 在用動態規劃解題時,我們往往將和子問題相關的各個變數的一組取值,稱之為一個“狀 態”。一個“狀態”對應於一個或多個子問題, 所謂某個“狀態”下的“值”,就是這個“狀 態”所對應的子問題的解。
- 所有“狀態”的集合,構成問題的“狀態空間”。“狀態空間”的大小,與用動態規劃解決問題的時間複雜度直接相關。 在數字三角形的例子裡,一共有N×(N+1)/2個數字,所以這個問題的狀態空間裡一共就有N×(N+1)/2個狀態。
整個問題的時間複雜度是狀態數目乘以計算每個狀態所需時間。在數字三角形裡每個“狀態”只需要經過一次,且在每個狀態上作計算所花的時間都是和N無關的常數。
3 確定一些初始狀態(邊界狀態)的值
以“數字三角形”為例,初始狀態就是底邊數字,值就是底邊數字值。
4 確定狀態轉移方程
定義出什麼是“狀態”,以及在該“狀態”下的“值”後,就要找出不同的狀態之間如何遷移――即如何從一個或多個“值”已知的 “狀態”,求出另一個“狀態”的“值”(遞推型)。狀態的遷移可以用遞推公式表示,此遞推公式也可被稱作“狀態轉移方程”。
數字三角形的狀態轉移方程:
能用動態規劃解決的問題的特點
1) 問題具有最優子結構性質。如果問題的最優解所包含的 子問題的解也是最優的,我們就稱該問題具有最優子結 構性質。
2) 無後效性。當前的若干個狀態值一旦確定,則此後過程的演變就只和這若干個狀態的值有關,和之前是採取哪種手段或經過哪條路徑演變到當前的這若干個狀態,沒有關係。
好久沒看部落格發現這篇文章現在已經這麼火熱了,看了一下評論發現不少人對這篇文章都比較有興趣,我當初寫這篇文章是受到了Coursera上面一門演算法課程的啟發,大家有興趣可以去聽聽這門課程:資料結構與演算法