動態規劃相信大家都知道，動態規劃演算法也是新手在剛接觸演算法設計時很苦惱的問題，有時候覺得難以理解，但是真正理解之後，就會覺得動態規劃其實並沒有想象中那麼難。網上也有很多關於講解動態規劃的文章，大多都是敘述概念，講解原理，讓人覺得晦澀難懂，即使一時間看懂了，發現當自己做題的時候又會覺得無所適從。我覺得，理解演算法最重要的還是在於練習，只有通過自己練習，才可以更快地提升。話不多說，接下來，下面我就通過一個例子來一步一步講解動態規劃是怎樣使用的，只有知道怎樣使用，才能更好地理解，而不是一味地對概念和原理進行反覆琢磨。

    首先，我們看一下這道題（此題目來源於北大POJ）：

    數字三角形(POJ1163)

    

在上面的數字三角形中尋找一條從頂部到底邊的路徑，使得路徑上所經過的數字之和最大。路徑上的每一步都只能往左下或 右下走。只需要求出這個最大和即可，不必給出具體路徑。 三角形的行數大於1小於等於100，數字為 0 - 99

    輸入格式：

    5      //表示三角形的行數    接下來輸入三角形

    7

    3   8

    8   1   0

    2   7   4   4

    4   5   2   6   5

    要求輸出最大和

    接下來，我們來分析一下解題思路：

    首先，肯定得用二維陣列來存放數字三角形

    然後我們用D( r, j) 來表示第r行第 j 個數字(r,j從1開始算)

    我們用MaxSum(r, j)表示從D(r,j)到底邊的各條路徑中，最佳路徑的數字之和。

    因此，此題的最終問題就變成了求 MaxSum(1,1)

    當我們看到這個題目的時候，首先想到的就是可以用簡單的遞迴來解題：

    D(r, j)出發，下一步只能走D(r+1,j)或者D(r+1, j+1)。故對於N行的三角形，我們可以寫出如下的遞迴式：   

1. if ( r == N)                  
2.     MaxSum(r,j) = D(r,j)    
3. else
4.     MaxSum( r, j) = Max{ MaxSum(r＋1,j), MaxSum(r+1,j+1) } + D(r,j)   

    根據上面這個簡單的遞迴式，我們就可以很輕鬆地寫出完整的遞迴程式碼： 

1. #include <iostream>  
2. #include <algorithm> 
3. #define MAX 101  
4. usingnamespace std;   
5. int D[MAX][MAX];    
6. int n;    
7. int MaxSum(int i, int j){      
8.     if(i==n)    
9.         return D[i][j];      
10.     int x = MaxSum(i+1,j);      
11.     int y = MaxSum(i+1,j+1);      
12.     return max(x,y)+D[i][j];    
13. }  
14. int main(){      
15.     int i,j;      
16.     cin >> n;      
17.     for(i=1;i<=n;i++)     
18.         for(j=1;j<=i;j++)          
19.             cin >> D[i][j];      
20.     cout << MaxSum(1,1) << endl;    
21. }        

    對於如上這段遞迴的程式碼，當我提交到POJ時，會顯示如下結果：

    

    對的，程式碼執行超時了，為什麼會超時呢？

    答案很簡單，因為我們重複計算了，當我們在進行遞迴時，計算機幫我們計算的過程如下圖：

    

    就拿第三行數字1來說，當我們計算從第2行的數字3開始的MaxSum時會計算出從1開始的MaxSum，當我們計算從第二行的數字8開始的MaxSum的時候又會計算一次從1開始的MaxSum，也就是說有重複計算。這樣就浪費了大量的時間。也就是說如果採用遞規的方法，深度遍歷每條路徑，存在大量重複計算。則時間複雜度為 2的n次方,對於 n = 100 行，肯定超時。 

    接下來，我們就要考慮如何進行改進，我們自然而然就可以想到如果每算出一個MaxSum(r,j)就儲存起來，下次用到其值的時候直接取用，則可免去重複計算。那麼可以用n方的時間複雜度完成計算。因為三角形的數字總數是 n(n+1)/2

    根據這個思路，我們就可以將上面的程式碼進行改進，使之成為記憶遞迴型的動態規劃程式： 

1. #include <iostream>  
2. #include <algorithm> 
3. usingnamespace std;  
4. #define MAX 101
5. int D[MAX][MAX];      
6. int n;    
7. int maxSum[MAX][MAX];  
8. int MaxSum(int i, int j){        
9.     if( maxSum[i][j] != -1 )           
10.         return maxSum[i][j];        
11.     if(i==n)     
12.         maxSum[i][j] = D[i][j];       
13.     else{      
14.         int x = MaxSum(i+1,j);         
15.         int y = MaxSum(i+1,j+1);         
16.         maxSum[i][j] = max(x,y)+ D[i][j];       
17.     }       
18.     return maxSum[i][j];   
19. }   
20. int main(){      
21.     int i,j;      
22.     cin >> n;      
23.     for(i=1;i<=n;i++)     
24.         for(j=1;j<=i;j++) {         
25.             cin >> D[i][j];         
26.             maxSum[i][j] = -1;     
27.         }      
28.     cout << MaxSum(1,1) << endl;   
29. }   

    當我們提交如上程式碼時，結果就是一次AC

    

    雖然在短時間內就AC了。但是，我們並不能滿足於這樣的程式碼，因為遞迴總是需要使用大量堆疊上的空間，很容易造成棧溢位，我們現在就要考慮如何把遞迴轉換為遞推，讓我們一步一步來完成這個過程。

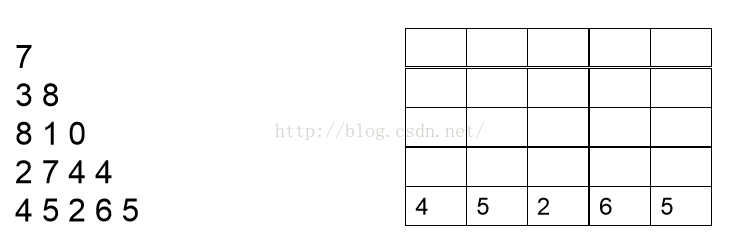
    我們首先需要計算的是最後一行，因此可以把最後一行直接寫出，如下圖：

    

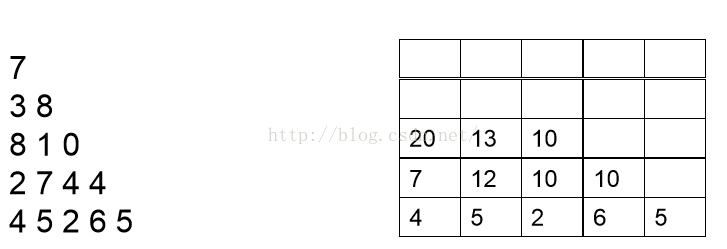
    現在開始分析倒數第二行的每一個數，現分析數字2，2可以和最後一行4相加，也可以和最後一行的5相加，但是很顯然和5相加要更大一點，結果為7，我們此時就可以將7儲存起來，然後分析數字7，7可以和最後一行的5相加，也可以和最後一行的2相加，很顯然和5相加更大，結果為12，因此我們將12儲存起來。以此類推。。我們可以得到下面這張圖：

    

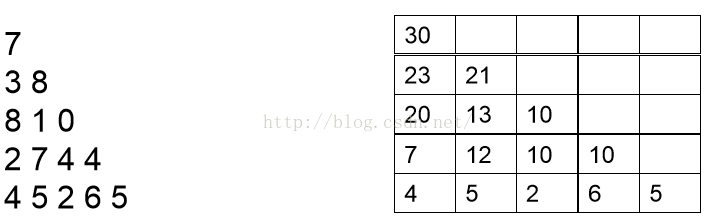
    然後按同樣的道理分析倒數第三行和倒數第四行，最後分析第一行，我們可以依次得到如下結果：

    

    

    上面的推導過程相信大家不難理解，理解之後我們就可以寫出如下的遞推型動態規劃程式： 

1. #include <iostream>  
2. #include <algorithm> 
3. usingnamespace std;   
4. #define MAX 101  
5. int D[MAX][MAX];     
6. int n;    
7. int maxSum[MAX][MAX];   
8. int main(){      
9.     int i,j;      
10.     cin >> n;      
11.     for(i=1;i<=n;i++)     
12.         for(j=1;j<=i;j++)          
13.             cin >> D[i][j];     
14.     for( int i = 1;i <= n; ++ i )       
15.         maxSum[n][i] = D[n][i];     
16.     for( int i = n-1; i>= 1;  --i )       
17.         for( int j = 1; j <= i; ++j )           
18.             maxSum[i][j] = max(maxSum[i+1][j],maxSum[i+1][j+1]) + D[i][j];      
19.     cout << maxSum[1][1] << endl;    
20. }   

     我們的程式碼僅僅是這樣就夠了嗎？當然不是，我們仍然可以繼續優化，而這個優化當然是對於空間進行優化，其實完全沒必要用二維maxSum陣列儲存每一個MaxSum(r,j),只要從底層一行行向上遞推，那麼只要一維陣列maxSum[100]即可,即只要儲存一行的MaxSum值就可以。

     對於空間優化後的具體遞推過程如下：

    

    

    

    

    

    

    接下里的步驟就按上圖的過程一步一步推導就可以了。進一步考慮，我們甚至可以連maxSum陣列都可以不要，直接用D的第n行直接替代maxSum即可。但是這裡需要強調的是：雖然節省空間，但是時間複雜度還是不變的。

    依照上面的方式，我們可以寫出如下程式碼：    

1. 相關推薦

   教你徹底學會動態規劃——入門篇

       動態規劃相信大家都知道，動態規劃演算法也是新手在剛接觸演算法設計時很苦惱的問題，有時候覺得難以理解，但是真正理解之後，就會覺得動態規劃其實並沒有想象中那麼難。網上也有很多關於講解動態規劃的文章，大多都是敘述概念，講解原理，讓人覺得晦澀難懂，即使一時間看懂了，發現當

   從 poj 1163（ The Triangle ）教你徹底學會動態規劃——入門篇

   動態規劃相信大家都知道，動態規劃演算法也是新手在剛接觸演算法設計時很苦惱的問題，有時候覺得難以理解，但是真正理解之後，就會覺得動態規劃其實並沒有想象中那麼難。網上也有很多關於講解動態規劃的文章，大多都是敘述概念，講解原理，讓人覺得晦澀難懂，即使一時間看懂了，發現當自己做題的時

   （poj-1163）教你徹底學會動態規劃——入門篇

    動態規劃相信大家都知道，動態規劃演算法也是新手在剛接觸演算法設計時很苦惱的問題，有時候覺得難以理解，但是真正理解之後，就會覺得動態規劃其實並沒有想象中那麼難。網上也有很多關於講解動態規劃的文章，大多都是敘述概念，講解原理，讓人覺得晦澀難懂，即使一時間看懂了，發現當自己做

   教你徹底學會動態規劃——進階篇

   ret 簡單 aik 原理 初始 cin while iostream urn 在我的上一篇文章中已經詳細講解了動態規劃的原理和如何使用動態規劃解題。本篇文章，我將繼續通過例子來讓大家更加熟練地使用動態規劃算法。 話不多說，來看如下例題，也是在動態規劃裏面遇

   教你徹底學會動態規劃

   部落格轉自：http://lib.csdn.net/article/datastructure/9390  動態規劃相信大家都知道，動態規劃演算法也是新手在剛接觸演算法設計時很苦惱的問題，有時候覺得難以理解，但是真正理解之後，就會覺得動態規劃其實並沒有想象中那麼難。網上

   教你徹底學會c語言動態規劃——進階篇

   今天小編給大家帶來了c語言動態規劃的進階篇。溫馨提示：亮點在最後！   如果想學c++並想學好，可以加這個群，首先是玖四捌，中間是玖伍四，最後是四捌四，裡面有大量的學習資料可以下載。 在我的上一篇文章中已經詳細講解了動態規劃的原理和如何使用動態規劃解題。本篇文章，我將繼續

   你必須學會的okhttp——入門篇

   早在畢業那段期間，群裡有很多小夥伴在問關於okhttp的問題，當時因為不瞭解。所以沒有回答的上。記得十月份有次面試，一個面試官問我關於網路請求的東西時，我記得當時我是說。我是通過HttpClient封裝了一個網路請求的工具類。當然，或許他想問的是我關於okhtt

   android之儲存篇_SQLite資料庫_讓你徹底學會SQLite的使用

   SQLite最大的特點是你可以把各種型別的資料儲存到任何欄位中，而不用關心欄位宣告的資料型別是什麼。例如：可以在Integer型別的欄位中存放字串，或者在布林型欄位中存放浮點數，或者在字元型欄位中存放日期型值。 但有一種情況例外：定義為INTEGER PRIMARY KEY的

   動態規劃入門（一）

   spa turn color and uil ott c++ erro 大數字 2017-09-01 11:29:43 writer：pprp 看sprout臺灣大學acm教學視頻的第一部分： 裏邊涉及到四道小例題 感覺很好就拿來寫了寫： 題意還有代碼說明都在代碼中： 1、

   [LeetCode] 動態規劃入門題目

   -- 解決 經典的 必須 重新 tps fit 等等 return 最近接觸了動態規劃這個厲害的方法，還在慢慢地試著去了解這種思想，因此就在LeetCode上面找了幾道比較簡單的題目練了練手。 首先，動態規劃是什麽呢？很多人認為把它稱作一種“算法”，其實我認為把它稱作一種“

   動態規劃入門

   記憶 重要 滿足 最優化策略 ogr 描述 背包 決策 背包問題 動態規劃入門 什麽是動態規劃？ 動態規劃(dynamic programming)是求解決策過程(decision process)最優化的數學方法。把多階段過程轉化為一系列單階段問題，利用各階段之間的關

   有趣的動態規劃入門解釋

   .cn .com 現在 消息 com 描述 容量 不但 情況下 今天在網上看到一個講動態規劃的文章，是以01背包為例的，這文章和書上的講解非常不一樣，令我眼前一亮，於是轉載一下下～～～附上原文地址：http://www.cnblogs.com/sdjl/articles/1

   動態規劃入門講稿

   代碼 常見 窮舉 依賴 rdquo www. 技巧 順序 衍生 目錄 第一講 01背包問題 第二講 完全背包問題 第三講 多重背包問題 第四講 混合三種背包問題 第五講 LIS問題 第一講:01背包 問題描述：有N件物品和一個容量為V的背包。第i件物品的費用

   手把手教你jmeter壓測--適合入門

   個數 gpo image .cn 發出 是我 gre target src 【後臺測試】手把手教你jmeter壓測 我知道我遲早是要踏上了後臺測試之路的，只是沒想到來的這麽突然。新接手了一個項目，在第一版發出後，產品需要做運營活動拉量，因為我擔心突然的流量湧入是否會對後臺

   手把手教你製作GIF動態圖片【GIF教程】

   GIF動態圖片的原理就是在一段時間內顯示一系列圖片或者是幀，每一張圖或者幀都較前面那一張圖有些許的變化，當變化速度達到一定程度就產生這些圖片或者幀動起來的錯覺。小編今天所講的教程就是教大家如何錄製視訊，並將視訊分解成幀，從而再將其串起來，製作成GIF動態圖片的。這需要用到一款名為迅捷GIF製

   ACM動態規劃基礎篇

   文章目錄 1 前言 1.1 什麼是動態規劃 1.2 什麼時候要用動態規劃 2 斐波那契數列 $Fibonacci$ 2.1 引入 2.2 定義 2.3 遞迴分治解決 $Recursion$

   教你零基礎如何快速入門大資料技巧

     現在是大資料時代，很多人都想要學習大資料，因為不管是就業前景還是薪資都非常的不錯，不少人紛紛從其他行業轉型到大資料行業，那麼零 基礎的人也想要學習大資料怎麼辦呢？下面一起探討下零基礎如何快速入門大資料技巧吧。   很多人都需要學習大資料是需要有一定的基礎

   51nod 1007 正整數分組 動態規劃入門

   將一堆正整數分為2組，要求2組的和相差最小。 例如：1 2 3 4 5，將1 2 4分為1組，3 5分為1組，兩組和相差1，是所有方案中相差最少的。 01揹包 將每個數字的大小當作重量和價值 設總和為sum 揹包最大容量開為sum/2 為嘛？ 因為這一組數和另一組數的差要最小

   教你快速學會 Python 函式基礎知識

   一、函式基礎 簡單地說，一個函式就是一組Python語句的組合，它們可以在程式中執行一次或多次執行。Python中的函式在其他語言中也叫做過程或子例程，那麼這些被包裝起來的語句通過一個函式名稱來呼叫。 有了函式，我們可以在很大程度上減少複製及貼上程式碼的次數了（相信很多人在剛開始時都有這樣的

   動態規劃基礎篇--最長上升子序列

   今天我們要講的是最長上升子序列（LIS）。 【題目描述】 給定N個數，求這N個數的最長上升子序列的長度。 【樣例輸入】 7 2 5 3 4 1 7 6 【樣例輸出】 4 什麼是最長上升子序列？ 就是給你一個序列，請你在其中求出一段不斷嚴格上升的部分，它