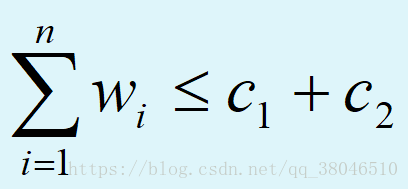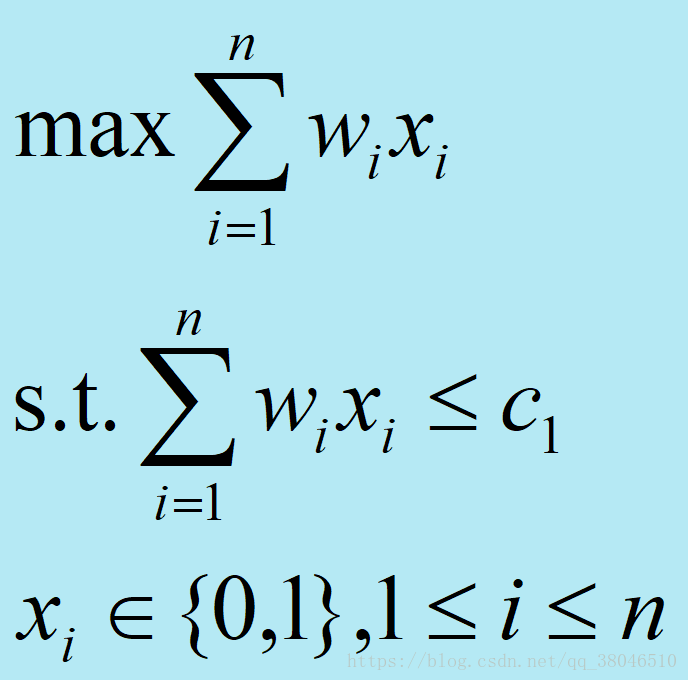問題描述：

一共有n個貨物要裝上兩艘重量分別為c1和c2的輪船上，其中貨物i的重量為Wi，且：

    要求確定是否有一個合理的裝載方案可將貨物裝上這兩艘輪船。

採取策略：      
 (1)首先將第一艘輪船儘可能裝滿；
 (2)將剩餘的集裝箱裝上第二艘輪船。將第一艘輪船儘可能裝滿等價於選取全體集裝箱的一個子集，
     使該子集中集裝箱重量之和最接近。由此可知，裝載問題等價於以下特殊的0-1揹包問題：

限界函式：

    定義一個CW表示到達當前結點O的重量，如果CW>C1，表示以O為根的子樹不能產生一個可行的解，避免移動。

缺陷：

    一個可行結點的右孩子總是可行。

演算法改進：

    如果當前結點的右子樹不可能包含比當前最優解更好的解，就不移動到右子樹上。

    設bestW為當前的最優解，Z為解空間樹的第i層的一個結點。

改進的限界函式：

    設r為剩餘貨箱的重量，當CW+r<=bestW時，沒有必要去搜索Z的右子樹。

話不多說，直接上程式碼：

package set;
public class Loading {
	static int n;//貨箱數目
	static int[] w;//貨箱重量陣列
	static int c;//第一艘船的重量
	static int cw;//當前裝載的重量
	static int bestw;//目前最優裝載的重量
	static int r;//剩餘貨箱的重量
	
	static int[] x;//當前解，記錄從根至當前結點的路徑
	static int[] bestx;//記錄當前最優解
	
	
	public static int MaxLoading(int[] ww,int cc) {
		//初始化資料成員，陣列下標從1開始
		n = ww.length - 1;
		w = ww;
		c = cc;
		cw = 0;
		bestw = 0;
		x = new int[n+1];
		bestx = new int[n+1];
		
		//初始化r，即剩餘最大重量
		for(int i =1;i<=n;i++) {
			r += w[i];
		}
		
		//計算最優載重量
		backtrack(1);
		return bestw;
	}
	
	//回溯演算法
	public static void backtrack(int t) {
		if(t>n) {//到達葉結點
			if(cw>bestw) {
				for(int i=1;i<=n;i++) {
					bestx[i] = x[i];
				}
				bestw = cw;
			}
			return;
		}
		
		r -= w[t];
		if(cw + w[t] <= c) {//搜尋左子樹
			x[t] = 1;
			cw += w[t];
			backtrack(t+1);
			cw -= w[t];//回溯
		}
		
		if(cw + r>bestw) {
			x[t] = 0;//搜尋右子樹
			backtrack(t+1);
		}
		
		r += w[t];//恢復現場
		
	}
	/*
	 * 如果當前節點的右子樹不可能包含比當前最優解更好的解時，就不移動到右子樹上！
	設bestw為當前最優解，Z為解空間樹的第i 層的一個節點
		為剩餘貨箱的重量;當cw+r<=bestw時，沒有必要去搜索Z 的右子樹：
		當前載重量cw+剩餘集裝箱的重量r當前最優載重量bestw
	 */
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] ww = {0,20,30,60,40,40};
		int c1 = 100;
		int c2 = 100;
		int n = ww.length - 1;
		
		MaxLoading(ww,c1);
		int weight2 = 0;//儲存第二艘船可能要裝的重量
		for(int i=1;i<=n;i++) {
			weight2 += ww[i]*(1-bestx[i]);//bestx[i]的值只能為0或1
			
		}
		if(weight2>c2) {
			System.out.println("無解");
		}
		else {
			System.out.println("第一艘船裝載貨物的重量： " + bestw);
			System.out.println("第二艘船裝載貨物的重量： " + weight2);
			
			//第一艘船的裝載情況
			for(int i = 1;i<=n;i++) {
				if(bestx[i] == 1) {
					System.out.println("第" + i + "件貨物裝入第一艘船");	
				}
			}
			
			//第二艘船的裝載情況
			for(int i = 1;i<=n;i++) {
				if(bestx[i] == 0) {
					System.out.println("第" + i + "件貨物裝入第二艘船");
					
				}
			}
			
		}
		
	}

}
 

執行結果：