深度搜索的應用----有向圖的連通性
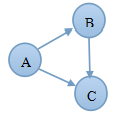
有向圖的連通性,首先看一下下面2個圖,
在圖1 中A->B-C->A,那麼我們就說這個有向圖存在環路。
在圖2中A->B->C, A->C,無法形成一個環路,則稱A,B,C三點不存在環路
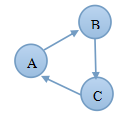
圖1 圖2
以下的例子是我自己臨時起意亂畫的,也不知道合適與否,有興趣的朋友講究看一下吧。^_^
從上面的圖可以明顯的看出,有向圖形成了一個環路,2-->8-->5-->3-->2(節點6作為一個單獨的節點沒有和任何節點有聯絡)
題目:判斷一個有向圖中是否存在環路,如果存在環路,列印環路中的一條通路的節點號並按升序排列,如果存在多條環路,只要列印其中一條環路即可。
例如上圖就列印:2,3,5,8
輸入:
8 7 //8代表節點數目,7代表有向圖的聯通路徑總數
1 4 4 2 2 7 2 8 8 5 5 3 3 2 //這組輸入資料代表有向圖的方向和連通性
1-->4
4-->22-->7
2-->8
8-->5
5-->3
3-->2
按照第二排輸入的資料,就可以畫出上面的有向圖的連線狀態
輸出:
2, 3,5,8
方法一:
一個節點一個節點去判斷是否形成環路:每次都是從第i個節點開始,例如:從節點i開始掃描,如果再次回到節點i,就說明形成了環路。
如果有10個節點就要掃描10次,如果有100個節點就要掃描100次,此種方法效率不是很高,但是容易理解。
掃描的方式我們採取深度搜索的方式。
具體程式碼如下:
- #include <iostream>
- using namespace std;
- bool success = false;
- bool isFinish = false;
- int visit[100];
- int AnswerN;
- int Answer[100];
- int N, M;
- int endNode;
- int A[100];
- int B[100];
- int array[100][100];
- void DFS(int array[100][100], int node)
- {
- //當發生遞迴的時候,說明i節點已經被被訪問,記錄下它當時的訪問狀態,1代表該節點已經被訪問過了
- visit[node] = 1;
- int i;
- for (i = 0; i < N; ++i)
- {
- //如果該標誌位為true表示已經深度搜索完成了,但是沒有形成環路
- isFinish = false;
- //如果已經形成了環路,則不需要進行後續的深度搜索
- if (success)
- {
- break;
- }
- //如果第node節點和第i節點存在連通性
- if (array[node][i] == 1)
- {
- //如果第i節點就是最終的節點,即找到了環路
- if (i == endNode)
- {
- success = true;
- //找到後,儲存該點,並加1,因為程式下標0開始的,加1後對應題目中的節點標號
- Answer[AnswerN++] = i + 1;
- break;
- }
- // 如果不存在環路,但是還有剩餘聯通的節點,則繼續進行深度搜索
- if( visit[i] == 0)
- {
- DFS(array, i);
- //只把形成環路的點,存貯到最後的結果中,多餘的點剔除在外
- if (isFinish == false)
- {
- Answer[AnswerN++] = i + 1;
- }
- }
- }
- //第node節點,i從0迴圈到N都沒有聯通,則沒有形成環路
- isFinish = true;
- }
- }
- int main()
- {
- int i, j;
- cin >> N >> M;
- for (i = 0; i < M; ++i)
- {
- cin >> A[i] >> B[i];
- }
- //初始化鄰接矩陣和訪問節點的標記位
- for (i = 0; i < N; ++i)
- {
- for (j = 0; j < N; ++j)
- {
- array[i][j] = 0;
- }
- visit[i] = 0;
- Answer[i] = 0;
- }
- //填入鄰接矩陣的值
- for (i = 0; i < M; ++i)
- {
- array[A[i] - 1][B[i] - 1] = 1;
- }
- AnswerN = 0;
- success = false;
- //對每個結點實施深度搜索
- for (i = 0; i < N; ++i)
- {
- //每次對i節點進行深度搜索,都要初始化visit陣列
- for (j = 0; j < N; ++j)
- {
- visit[j] = 0;
- }
- //起點也即終點
- endNode = i;
- DFS(array, i);
- //已經成環了,因為只要找到一條路徑,所以不再尋找後續的環路
- if (success)
- {
- break;
- }
- }
- if (success == false)
- {
- AnswerN = 0;
- }
- else
- {
- //如果存在環形佇列則排序
- for (i = 0; i < AnswerN; ++i)
- {
- for (j = i; j < AnswerN; ++j)
- {
- if (Answer[i] > Answer[j])
- {
- int tmp = Answer[i];
- Answer[i] = Answer[j];
- Answer[j] = tmp;
- }
- }
- }
- }
- //輸出最後的結果
- if (AnswerN == 0)
- {
- cout << "0 " << endl;
- }
- else
- {
- for (i = 0; i < AnswerN; ++i)
- {
- cout << Answer[i] << " ";
- }
- cout << endl;
- }
- return 0;
- }
方法二:
從第一個節點進行深度搜索,一次性走完該節點相關所有的深度搜索的節點。如果存在環路,直接從找出來,如果不存在環路,是否有剩餘未訪問的節點,如果有再進行深度搜索的遍歷。
相對來說該方法提高了效率,相當於深度搜索是每個聯通的資料塊,一個聯通的資料塊可能有環路,可能沒有環路,如果沒有環路,深度搜索下個聯通的資料塊。
具體程式碼如下:
- #include <iostream>
- using namespace std;
- bool success = false;
- int visit[100];
- int tree[100];
- int AnswerN;
- int Answer[100];
- int N, M;
- int A[100];
- int B[100];
- int array[100][100];
- int DFS(int array[100][100], int node)
- {
- visit[node] = 1;
- int i;
- int t;
- for (i = 0; i < N; ++i)
- {
- //如果第node節點和第i節點存在連通性
- if (array[node][i] == 1)
- {
- //如果找到了環路
- if (visit[i] == 1)
- {
- Answer[AnswerN++] = node;
- //找node節點的父節點
- int w = tree[node];
- //迴圈查詢父節點,追溯至源頭
- while (w != tree[w])
- {
- //父節點就是i節點,即此時形成了環路
- if (w == i)
- {
- Answer[AnswerN++] = w;
- return 1;
- }
- Answer[AnswerN++] = w;
- w = tree[w];
- }
- if (w == i)
- {
- Answer[AnswerN++] = w;
- return 1;
- }
- }
- else //如果沒有被訪問過,則再進行深度搜索
- {
- //記錄下i節點的父親節點node,即node是i的父節點
- tree[i] = node;
- t = DFS(array, i);
- if (t == 1)
- {
- return 1;
- }
- }
- }
- }
- return 0;
- }
- int main()
- {
- int i, j;
- cin >> N >> M;
- for (i = 0; i < M; ++i)
- {
- cin >> A[i] >> B[i];
- }
- for (i = 0; i < N; ++i)
- {
- for (j = 0; j < N; ++j)
- {
- array[i][j] = 0;
- }
- visit[i] = 0;
- Answer[i] = 0;
- //初始化父節點
- tree[i] = i;
- }
- for (i = 0; i < M; ++i)
- {
- array[A[i] - 1][B[i] - 1] = 1;
- }
- AnswerN = 0;
- for (i = 0; i < N; ++i)
- {
- //判斷剩餘的訪問節點,如果沒有被訪問則再進行深度遍歷,如果已經被訪問了就不會訪問該節點了
- if (visit[i] == 0)
- {
- if (1 == DFS(array, i))
- {
- success = true;
- break;
- }
- }
- success = false;
- }
- if (success == false)
- {
- AnswerN = 0;
- }
- else
- {
- //如果存在環形佇列則排序
- for (i = 0; i < AnswerN; ++i)
- {
- for (j = i; j < AnswerN; ++j)
- {
- if (Answer[i] > Answer[j])
- {
- int tmp = Answer[i];
- Answer[i] = Answer[j];
- Answer[j] = tmp;
- }
- }
- }
- }
- if (AnswerN == 0)
- {
- cout << "0" << endl;
- }
- else
- {
- for (i = 0; i < AnswerN; ++i)
- {
- cout << Answer[i]+1 << " ";
- }
- cout << endl;
- }
- return 0;
- }
最後給出幾個參考用例
5 5
4 3 2 4 3 5 3 2 1 4 //輸出 2 3 4
5 5
4 3 2 4 3 5 2 3 1 4 //輸出0
6 5
1 5 6 4 3 1 5 3 4 6 //輸出 1 3 5